
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лінійна засічка
|
|
|
|
У лінійній засічці вимірюються відстані 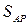 і
і 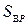 до точки, яка визначається від двох точок A і B з відомими координатами
до точки, яка визначається від двох точок A і B з відомими координатами  і
і  . Графічно рішення знаходиться як точка перетину кола з центром у точці А радіусом
. Графічно рішення знаходиться як точка перетину кола з центром у точці А радіусом 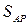 та кола з центром в точці B радіусу
та кола з центром в точці B радіусу 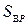 . Цих точок перетину кіл виходить дві – P- ліва і P -права (рис. 6.4). Потрібна точка вибирається по розташуванню (ліворуч або праворуч) відносно прямої напрямку AB.
. Цих точок перетину кіл виходить дві – P- ліва і P -права (рис. 6.4). Потрібна точка вибирається по розташуванню (ліворуч або праворуч) відносно прямої напрямку AB.
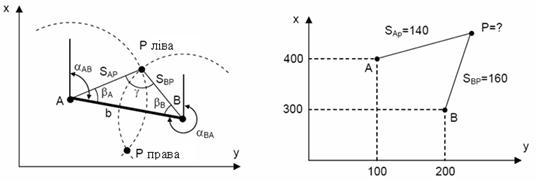
Рисунок 6.4 – Лінійна засічка
Для аналітичного рішення лінійної засічки вирішимо зворотню геодезичну задачу між точками A і B: визначимо дирекційні кути 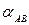 і
і 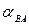 , а також відстань b між точками A і B. Обчислимо кути
, а також відстань b між точками A і B. Обчислимо кути 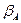 і
і 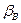 , скориставшись теоремою косинусів:
, скориставшись теоремою косинусів:
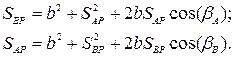 (6.6)
(6.6)
Далі потрібно знайти дирекційні кути сторін AP і BP. Якщо точка, яку визначаємо розташована праворуч від лінії AB, то 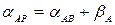 ,
, 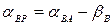 . Якщо точка, яку визначаємо розташована ліворуч від лінії AB, то
. Якщо точка, яку визначаємо розташована ліворуч від лінії AB, то 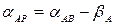 ,
, 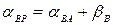 . Тепер для визначення координат точки P можна вирішити пряму геодезичну задачу з точки A на P і з точки B на P. Отримані два рішення повинні співпасти. У прикладі на рис. 6.4 дирекційний кут
. Тепер для визначення координат точки P можна вирішити пряму геодезичну задачу з точки A на P і з точки B на P. Отримані два рішення повинні співпасти. У прикладі на рис. 6.4 дирекційний кут 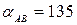 , кут
, кут  , кут
, кут 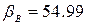 , а відстань між точками A і B – 141,42 м. Вирішуючи пряму геодезичну задачу від точки A, одержимо координати точки P – (457, 227).
, а відстань між точками A і B – 141,42 м. Вирішуючи пряму геодезичну задачу від точки A, одержимо координати точки P – (457, 227).
6.3 Фотограмметрія
Фотограмметрія – технічна дисципліна, основною метою якої є визначення виду і розмірів будь-якого об'єкта шляхом вивчення і вимірювання його фотографічного зображення, – знайшла найбільше застосування в топографії, де об'єктом вивчення і вимірювання є місцевість. Завдання фотограмметрії – замінити польові виміри, необхідні для створення карти, вимірами аерофотографії або космічного знімка в камеральних умовах за допомогою спеціальних фотограмметричних приладів і програмного забезпечення.
Методи фотограмметрії почали розроблятися в середині XIX століття з виникненням техніки фотографії. До появи літаків фотограмметрія використовувалася для пошуку взаємозв'язків між звичайними фотографіями і великого практичного значення не мала. З розвитком повітроплавання на початку XX століття виникла потреба поєднувати зроблені з літального апарату фотографії з картами. В аналоговій фотограмметрії для побудови топографічних карт і тривимірних об'єктів за двома знімкам, які перекриваються використовувалися оптичні і механічні прилади. В аналітичній фотограмметрії деякі дорогі компоненти системи фотограмметричної обробки замінялися комп'ютером, а аналогові виміри – математичними обчисленнями.
Цифрова фотограмметрія працює з цифровими зображеннями, які отримуються шляхом сканування аерокосмічних фотографій або безпосередньо з цифрової камери. Методи цифрової фотограмметрії дозволяють ще сильніше автоматизувати процес підготовки фотокарт і ортопланів, а також отримувати нові ГІС-продукти, наприклад, цифрові моделі рельєфу. Частина фотограмметрії, яка вивчає способи визначення висоти об'єкта і вимірювання характеристик рельєфу, називається стереофотограмметрією.
Використання даних дистанційного зондування Землі значно спрощує і здешевлює процес створення топографічних карт і дає принципово нові можливості для тематичного картографування. Космічний знімок можна розглядати як деяку картографічну проекцію земної поверхні. Якщо перетворити знімок таким чином, щоб його «проекція» відповідала проекції створюваної карти або шару ГІС, цей знімок можна буде безпосередньо використовувати спільно з іншими шарами. Так можна проводити ручне дешифрування отриманих з космосу фотографій по підкладці, відображати на топографічній основі результати обробки та аналізу знімків, поєднувати при візуалізації векторні карти і растрові знімки. Накладаючи на фотокарту шари гідрографії і автодоріг, виходить досить наочний ГІС-продукт.
Безпосередньо поєднувати космічні фотографії та карти не можна, тому що знімки містять різні деформації. На геометричні спотворення космічних знімків впливає низка факторів. На знімках в центральній проекції цими чинниками є кут нахилу і кривизна Землі. На космічних сканованих знімках факторів, що впливають на геометрію зображення, стає значно більше. Якщо зйомка декількох послідовних сцен виконується безупинно в часі, велике значення має власне обертання Землі, яке приводить до деформації форми ділянок поверхні, яка фотографується. Також необхідно враховувати час формування рядка, закони проектування під час зйомки, спосіб візуалізації.
Постачальники космічних знімків надають користувачам зображення з різним рівнем корекції. Наприклад, рівень 1A сцени, отриманої зі супутника SPOT, означає, що зображення, отримане безпосередньо з камери, виконано з радіометричною корекцією. Зображення рівня 1B відкоректовані з урахуванням обертання Землі, кута зйомки.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 4146; Нарушение авторских прав?; Мы поможем в написании вашей работы!