Зовнішнє орієнтування знімка

Основою цього етапу фотограмметричної обробки служать рівняння переходу від плоских координат растрового зображення до просторових декартових координат об'єкту. Зовнішнє орієнтування знімка визначає зв'язок растрового зображення і топографічної координатної системи. Шість змінних, які визначають позицію і орієнтацію зображення у момент зйомки, називають елементами зовнішнього орієнтування знімка.

Змінні описують позицію точки центру перспективи знімка O в топоцентричній системі координат. Змінна показує висоти камери над рівнем моря і залежить від використовуваного геодезичного датуму. Інші три елементи зовнішнього орієнтування є кутовими і визначають положення площини зображення відносно площини топографічної системи координат.

На рис. 6.7 – кут повороту площині зображення навколо осі oX фотографії; – кут повороту площини зображення навколо осі oY фотографії; 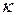– кут повороту площини зображення навколо осі oZ фотографії.

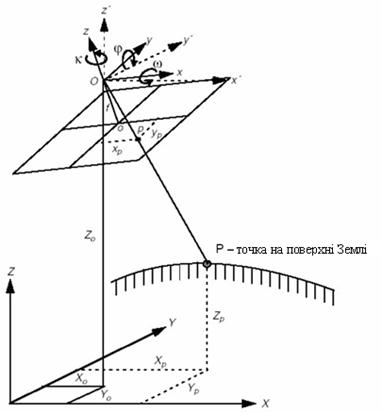
Рисунок 6.7 – Елементи зовнішнього орієнтування знімка

Елементи зовнішнього орієнтування знімка визначають з умов колінеарності променів, які проектують, якщо на знімку зображені не менш 3 опорних точок з відомими геодезичними координатами:

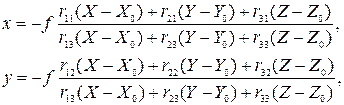
де – координати зображення; 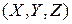– геодезичні координати, – фокусна відстань; – геодезичні координати центру перспективи; 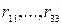– елементи матриці повороту, заданої кутами .

Для відновлення епіполярних площин стереопари, побудови геометричної моделі і отримання стереоскопічного зображення, необхідно взаємне орієнтування одного знімка щодо іншого. Знімки зазвичай лише приблизно горизонтальні, тому на початку процедури взаємного орієнтування відповідні проектуючі промені двох знімків не перетинаються, що призводить до появи вертикальних паралаксів. Горизонтальний паралакс можна усунути зміною висоти площини проектування, вертикальний паралакс свідчить про неправильне взаємне орієнтування.

6.4 Контрольні запитання та завдання

1. Що вивчає наука геодезія?

2. Наведіть основні геодезичні засічки.

3. Які вихідні дані, вимірювані та невідомі елементи у полярної засічки?

4. Які вихідні дані, вимірювані та невідомі елементи у прямої кутової засічки?

5. Які вихідні дані, вимірювані та невідомі елементи у лінійної засічки?

6. Опишіть внутрішню геометрію зображення, зробленого камерою.

7. Опишіть процес перетворення піксельних координат у систему координат зображення.

8. Наведіть елементи зовнішнього орієнтування знімка.

7 Фізична поверхню Землі і референцної системи координат

План лекції: Геодезичні системи координат і висот. Системи координат, які використовуються в Україну. Місцеві системи координат. Системи координат, які використовуються в європейській та світовій практиці. Зв'язок УСК-2000 з іншими системами координат.

7.1 Геодезичні системи координат і висот

Фізична поверхня Землі, як і інших небесних тіл, має складну форму (рис. 7.1).

Рисунок 7.1 – Фізична поверхня Землі

Її вивчення є першочерговою для багатьох наук, в тому числі математичної картографії.

При цьому використовується поняття про поверхню геоїда, яке ввів у 1873 році німецький фізик Лістинг. В даний час під поверхнею геоїда розуміють рівневу поверхню, що проходить через точку початку відліку висот.

Рівневою поверхнею називається поверхня, ортогональна до прямовисних ліній, за якими в кожній точці поверхні даного небесного тіла спрямований вектор сили тяжіння. Суворе визначення геоїда пов'язане із знанням будови земної кори.

М.С. Молоденський запропонував замість геоїда визначати поверхню квазігеоїда, яку можна строго визначити без залучення різних гіпотез про будову земної кори і яка збігається з поверхнею геоїда на морях і океанах і відступає від неї до 2 метрів на континентальній частині.

Рисунок 7.2 – Подання геоїда

1 геоїд; 2 загальний земний еліпсоїд; 3 референц-еліпсоїд

У геодезії вимірювання, виконані на фізичній поверхні, переносять на математичну, найбільш близьку до фізичної, яка може бути описана відповідними рівняннями. У зв'язку з цим вивчають і використовують загальноземний еліпсоїд і референц-еліпсоїди (рис. 7.2).

Еліпсоїд обертання, площина екватора і центр якого збігається з площиною екватора і центром мас Землі і найкращим чином апроксимує поверхню геоїда (квазігеоїда) в планетарному масштабі, називається загальноземним еліпсоїдом.

Еліпсоїд, на поверхню якого відображаються матеріали астрономо-геодезичних робіт і топографічних зйомок, і який найбільш повно відповідає поверхні геоїда на відповідній території Землі, називається референц-еліпсоїдом. Ці поверхні називаються так само поверхнями відносності. У різних країнах прийняті свої референц-еліпсоїди, що розрізняються своїми параметрами.

У математичній картографії, щоб відобразити на площині фізичну поверхню Землі та інших реальних поверхонь, необхідно від цих поверхонь перейти до математичних. В якості таких поверхонь беруть поверхню кулі, еліпсоїда обертання, і в окремих випадках – тривісного еліпсоїда.

До елементів геодезичної основи відносять опорні пункти, визначені в системі геодезичних координат, прийнятої в даній державі, і координатні сітки, пов'язані з цими опорними пунктами.

Геодезичні системи координат включають:

• параметри референц-еліпсоїда (величина великої півосі 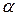або малої 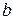, стиснення 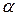або ексцентриситет );

• висоту геоїда над референц-еліпсоїдом в початковому пункті;

• вихідні геодезичні дати (геодезичні широта і довгота початкового пункту, азимут на орієнтирний пункт).

У процесі складання карт визначають геодезичну систему координат і систему висот, які були прийняті при створенні вихідного картографічного матеріалу. Це виявляється за формуляром аркушів карт або за літературно-описовими джерелами.

У випадках коли геодезична основа вихідного матеріалу, який використовується для створення карт, має іншу геодезичну систему координат, необхідно здійснити перетворення цієї системи в геодезичну систему координат, прийняту в даній державі.

Це завдання, як правило, вирішується аналітично – шляхом запровадження так званих диференціальних поправок першого і другого роду. В багатьох книгах по вищій і сферичній геодезії дані формули для визначення диференціальних поправок першого роду , які враховують зміни початку координат і азимута в початковому (вихідному) пункті, і другого роду 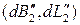, які враховують зміни стиснення і великої півосі вихідного і нового еліпсоїдів. В даний час розроблені і використовуються алгоритми таких перетворень з проміжним переходом у геоцентричні координати.

7.2 Системи координат, які використовуються в Україні

Референцна система координат 1942 року (СК-42). Система координат 1942 року – референцна система прямокутних координат на площині, яка базується на використанні конформної проекції Ґаусса-Крюгера з вихідними даними:

· референц-еліпсоїд Красовського – велика піввісь 6 378 245 м, стиснення 1:298.3;

· висота геоїда в Пулково над референц-еліпсоїдом дорівнює нулю;

· геодезичні координати Пулковської обсерваторії (центр сигналу А): широта — 59°46′18.22″, довгота від Ґрінвіча 30°19′33.79″;

· геодезичний азимут з Пулково на пункт – Бугри – 121°10'38'',79; Центр еліпсоїда Красовського збігається з початком референцної СК, вісь обертання еліпсоїда рівнобіжна (паралельна) вісі обертання Землі, а площина нульового меридіана визначає положення початку відліку довготи. Всі інші параметри еліпсоїда є похідними.

Державна нівелірна мережа поширюється на всю територію країни систему нормальних висот (Балтійська система 1977 року), вихідним початком якої є нуль Кронштадтського футштока. Прямокутні координати Державної геодезичної мережі обчислювалися на площині в конформній проекції Ґаусса-Крюгера в шестиградусних зонах, вісьовими меридіанами є меридіани з довготами 21°, 27°, 33°, 39°. Початком координат у кожній зоні є точка перетину вісьового меридіану з екватором. Значення ординати на вісьовому меридіані приймається рівним 500 км.

При топографічній зйомці у масштабах 1:5 000 і більше крім прямокутних координат у шестиградусних зонах обчислюються прямокутні координати у триградусних зонах. Вісьовими меридіанами цих зон у системі координат 1942 року є меридіани з довготами 21°, 24°, 27°, 30°... 39°.

Референцна система координат 1963 року (СК-63). Умовна система координат СК-63 ґрунтується на триградусних зонах, є відкритою системою і у відповідності до діючих нормативно-технічних документів рекомендована як основна для кадастрових знімань. Практичне застосування СК-63 ускладнюється можливістю попадання крупних об'єктів картографування в декілька зон, а також "таємністю" параметрів переходу ("ключів") від державної системи координат до СК-63 при відкритості самих координат в СК-63. Це спеціально спотворена СК, яка базувалася на проекції Ґаусса-Крюгера і СК 1942 року. За математичною сутністю — це та ж система Ґаусса-Крюгера, тільки номенклатура базових карт масштабу 1:100 000 побудована по-іншому.

Прив'язуються топографічні карти СК-63 до стандартної системи СК-42, виходячи з того, що обидві системи ґрунтуються на системі координат Ґаусса-Крюгера, рамки аркушів розбиті по географічній сітці, а зміщення сітки кратні цілому числу мінут (одна мінута вздовж меридіана дорівнює 1 морській милі або 1 852 метрам; довжина мінути уздовж паралелі зменшується до півночі і на середніх широтах становить приблизно половину милі). При використанні деяких сучасних методів визначення місцеположення (GPS) необхідно вносити відповідні поправки у результаті вимірювань для переходу в систему СК-63.

7.3 Місцеві системи координат

Положення про порядок встановлення місцевих систем координат було затверджено наказом Мінекоресурсів від 03.07.2001 року за № 245. Місцеві системи координат встановлюються з метою мінімального спотворення проекції Ґаусса-Крюгера, зручності у використанні і застосовуються при виконанні топографо-геодезичних робіт та створенні топографічних планів у масштабах 1:5 000, 1:2 000, 1:1 000 та 1:500 на території міст та інших населених пунктів, промислових комплексів усіх галузей економіки, підприємств гірничодобувної та нафтодобувної промисловості.

Встановлення нової або внесення змін до існуючої місцевої системи координат проводиться у випадках:

· якщо на об'єктах не виконувались топографо-геодезичні роботи і відповідно не були встановлені місцеві системи координат;

· якщо місцеві системи були не зв'язані з державними системами;

· якщо об'єкти примикають один до одного і для кожного з них була встановлена своя місцева система координат.

Для встановлення нової місцевої системи координат приймається проекція Ґаусса-Крюгера з довільним вісьовим меридіаном, що проходить через центральну частину або поблизу об'єкта робіт шляхом перерахунку/переобчислення координат системи 1942 року з таким розрахунком, щоб поправками за редукування ліній та кутів на площину у цій проекції можна було знехтувати. Якщо територія об'єкта робіт знаходиться на краю триградусної зони або у двох суміжних зонах, то довільним треба вважати найближчий роздільний вісьовий меридіан.

Місцева система координат утворюється від переобчислених координат системи 1942 року шляхом введення відповідного "ключа" переходу таким чином, щоб координати в місцевій системі складалися в метрах з п'ятизначних цифр, були додатні, а величини абсцис були в два рази більші від ординат.

Державна геодезична референцна система координат УСК-2000. Система координат УСК-2000 утворена від ITRS/ITRF2000. За відліковий еліпсоїд у ній прийнято референц-еліпсоїд Красовського з параметрами: велика піввісь еліпсоїда – 6 378 245 м; стиснення еліпсоїда - 1:298,3.

Система координат УСК-2000 чітко узгоджена з Міжнародною загальноземною референцною системою координат ITRS на епоху 2000 року – ITRF2000, яка закріплена пунктами космічної геодезичної мережі. УСК-2000 встановлена для виконання топографо-геодезичних та картографічних робіт на території України постановою Кабінету Міністрів України "Деякі питання застосування геодезичної системи координат" від 22 вересня 2004 р. № 1259. З моменту введення системи координат УСК-2000 при виконанні нових робіт вона замінила систему координат 1942 року, яка була введена постановою Ради Міністрів СРСР № 760 від 7 квітня 1946 року.

УСК-2000 отримана в результаті сумісного вирівнювання пунктів Української перманентної мережі спостережень глобальних навігаційних супутникових систем та Державної геодезичної мережі 1-4 класів на епоху 2005 року і закріплена пунктами Державної геодезичної мережі.

Положення пунктів у прийнятій системі координат визначається:

· просторовими прямокутними координатами X, Y, Z (вісь Z співпадає з віссю обертання еліпсоїда, вісь X лежить в площині нульового меридіану, а вісь У доповнює систему до правої; початком системи координат є геометричний центр еліпсоїда);

· геодезичними (еліпсоїдальними) координатами: широтою — В, довготою – L, висотою – H;

· плоскими прямокутними координатами х та у, які обчислюються в проекції Ґаусса-Крюгера;

· геодезична висота Н утворюється як сума нормальної висоти та висоти квазігеоїда над еліпсоїдом Красовського. Нормальні висоти геодезичних пунктів визначаються в Балтійській системі висот 1977 року, вихідним початком якої є нуль Крондштадського футштоку, а висоти квазігеоїда обчислюються над еліпсоїдом Красовського.

7.4 Системи координат, що використовуються в європейській та світовій практиці

Міжнародна земна референцна система відліку (ITRF). ITRF — це загальноземна система відліку, яка задається та уточнюється Міжнародною службою обертання Землі (IERS). Вона визначається резолюцією №2, прийнятою на двадцятій генеральній асамблеї IUGG (International Union of Geodesy and Geophysics) у Відні в 1991 році. В IERF положення будь-якої точки на поверхні Землі задається таким чином: значення YY — це рік, дані якого були використані при реалізації системи. Наприклад, ITRF94 означає систему відліку, створену в 1995 році, для формування якої були використані дані за 1994 рік.

На даний час відомі такі реалізації системи ITRF: ITRF89, ITRF90, ITRF91, ITRF92, ITRF93, ITRF94,1TRF96, ITRF97, ITRF2000. Таким чином положення точки на епоху t буде:

.

Європейська земна референцна система координат (ETRS89). Підкомісія світової асоціації геодезії для Європи (EUREF), згідно своєї резолюції №1, прийнятої на зустрічі в м. Файерензі (Firenze) в 1990 році, рекомендувала, що загальноземна система відліку координат, яка буде прийнята EUREF, буде співпадати з системою ITRS на епоху 1989 та буде зафіксована на стабільній частині Євразійської плити. Ця система отримала назву Європейська земна референцна система відліку координат 89 (ETRS89).

Практична реалізація системи ETRS89 здійснена через мережу станцій розташованих по всій території Європи, які закріплюють дану систему координат.

7.5 Зв'язок УСК-2000 з іншими системами координат

Система координат ITRS. Геодезична референцна система координат України з системою FFRS-ITRF2000 однозначно пов'язана параметрами зв'язку, що отримані в результаті моделювання параметрів геодезичної референцної системи координат України.

Система координат ETRS89. Геодезична референцна система координат України з системою ETRS89 пов'язана параметрами зв'язку, які видаються комісією EUREF як параметри зв'язку ITRS-ETRS89.

Система координат СК-42. Банк геодезичних пунктів побудований таким чином, що дозволяє зберігати координати пунктів ДГМ в системі СК-42 та в новій геодезичній референцній системі координат. Для об'єктів, координати яких отримані в СК-42 і які не занесені в банк геодезичних даних, передбачається перетворення в нову систему з використанням локальних параметрів на основі TIN-моделі з подальшим інтерполюванням на основі регулярної сітки – GRID.

Система координат СК-63. Система координат 1963 р. не є класичною системою координат, а похідною від СК-42, і отримана відповідним алгоритмом перетворення. Різноманітні перетворення в межах системи СК-63 виконуються через систему СК-42. Оскільки система ведення банку геодезичних даних передбачає підтримання СК-42, то й в межах її точності є можливість підтримувати СК-63.

Місцеві системи координат. Місцеві системи координат, в основному, утворені від системи координат 1942 р. Для збереження математичної основи великомасштабних планів 1:500-1:5 000 при введенні нової геодезичної референцної системи координат пропонуються аналогічні дії, що і при створенні нової системи координат, а саме:

· побудова каркасної геодезичної мережі на територію населеного пункту з використанням супутникових радіонавігаційних систем та з обов'язковою її прив'язкою до ДГМ в новій системі координат;

· моделювання параметрів зв'язку (ключів переходу) місцевої системи з новою геодезичною референцною системою координат України за умов оптимального збереження існуючої місцевої системи координат;

· вирівнювання міських геодезичних систем координат з використанням результатів вимірів, виконаних у минулі роки;

· каталогізація пунктів міських геодезичних мереж, введення місцевої системи координат.

Таким чином, на даному етапі перед Україною постає складне завдання у виборі оптимального шляху перебудови національної системи відліку. Складність цього завдання обумовлюється такими основними факторами:

· з однієї сторони, необхідне оперативне впровадження в геодезичне виробництво нової високоточної системи відліку, що забезпечить ефективне використання супутникових радіонавігаційних систем та європейську інтеграцію з питань геопросторового представлення інформації;

· з другої сторони, в новій структурі системи відліку повинна бути максимально врахована можливість використання існуючої Державної геодезичної мережі, на створення якої були затрачені великі фінансові і трудові ресурси країни і яка є математичною основою загальнодержавного картографування території України.

Для території України, як основну координатну систему для відображення геопросторової інформації, пропонується використати Державну геодезичну референцну систему координат УСК-2000, для населених пунктів рекомендується використання місцевих систем координат, які утворені від системи УСК-2000.

7.6 Контрольні запитання та завдання

1. Наведіть визначення поняття «геоїд».

2. Наведіть визначення поняття «загальний земної еліпсоїд».

3. Які вихідними даними для СК42?

4. Наведіть визначення поняття «референц-еліпсоїд».

5. Які системи координат використовуються в Україні?

6. Які системи координат використовуються в європейській та світовій практиці?

7. Розкрийте зв'язок УСК-2000 з іншими системами координат.

8. Загальна теорія картографічних проекцій

План лекції: Системи координат прийняті в ГІС. Визначення картографічних проекцій, картографічні мережі. Нескінченно мала сфероїдична (сферична) трапеція і її зображення на площині. Масштаби. Умови відображення поверхні еліпсоїда (сфери) на площині. Спотворення картографічних проекцій. Методи перетворення картографічних проекцій при створенні карт ГІС. Фактори і способи вибору картографічних проекцій для створення карт ГІС.

Математична основа є одним з фундаментальних понять геоінформатики та ГІС. Наявність математичної основи карт ГІС є принциповою відмінністю ГІС від САПР та інших інформаційних систем. Саме математична основа (МО) дає можливість інтеграції різних даних, як на глобальному (загальноземному), так і на інших рівнях.

Технологічно МО є теоретичною базою побудови цифрових моделей та базових карт ГІС, забезпечує взаємооднозначну і топологічну відповідність просторових об'єктів і явищ природи і суспільства та їх зображення на картах.

Розробка МО, вибір і використання ґрунтується на прийнятій в даній країні геодезичних системах координат і висот, загальної теорії картографічних проекцій, теорії класів і окремих варіантів проекцій, а також інших елементів – головних масштабів, компонувань і разграфок карт.

При створенні карт ГІС необхідно, щоб вихідні картографічні матеріали були приведені в геодезичну систему координат і картографічну проекцію базової карти, прийняті для карт даної ГІС, її математична основа забезпечувала б оптимальні умови розв'язання задач ГІС по картах.

Коротко розглянемо основні положення.

8.1 Системи координат прийняті в ГІС

У теорії та практиці ГІС застосовуються прямокутні, криволінійні, плоскі прямокутні та полярні системи координат.

У довільній точці еліпсоїда проведемо нормаль 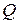О ' до цієї поверхні (рис. 8.1.), через яку можна провести безліч нормальних перетинів. З них ми виберемо два головних: перетин, який збігається з площиною меридіана Р 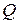Р' (меридіан) і перетин, який ортогональний першому в точці 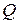(перетин першого вертикала). З урахуванням цього визначають і використовують різні системи координат: геодезичну, геоцентричну, топоцентричну, сфероїдичну (сферичну), ізометричну і локальні системи.

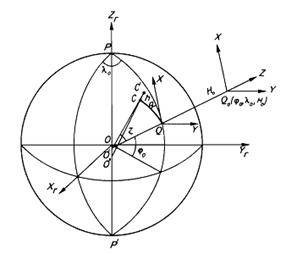
Рисунок 8.1 – Топоцентрична і сфероїдична полярні системи координат

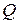У геодезичній системі визначається геодезична широта точки – кут між нормаллю О' до поверхні еліпсоїда в даній точці еліпсоїда 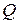й площиною екватора та довгота цієї точки – двохгранний кут між площинами початкового меридіана і меридіана даної точки. У просторовій геоцентричній системі координат початок поєднано з центром мас Землі (з центром еліпсоїда обертання), вісь 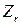– спрямована на середній північний полюс Землі, вісь – точку перетину Гринвіцького меридіана з екватором, вісь 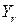– на схід.

Зв'язок геоцентричної та геодезичної системи координат виражається формулами:

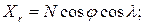
де – радіус кривизни перетину першого вертикала в даній точці; – відповідно велика піввісь еліпсоїда обертання і квадрат першого його ексцентриситету.

Топоцентричною системою координат (рис. 8.1.) будемо називати систему, в якій початок поєднано з довільною точкою простору 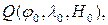вісь X лежить в площині меридіана точки 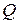і спрямована на північний (середній) полюс, вісь Z збігається з нормаллю 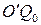до поверхні еліпсоїда в точці 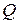, вісь Y – доповнює систему до лівої.

Формули зв'язку топоцентричної та геодезичної систем координат має вигляд:

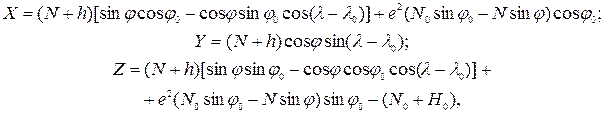
де – відповідно географічні координати в поточних точках і точці полюса; 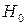– висота точки полюса відносно поверхні еліпсоїда;
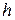– перевищення точок.

У сфероїдичній полярній системі координат , – кути між нормальними площинами у точці полюса 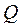, z – кути між нормаллю 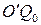і напрямом в точці 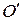на поточні точки С, що лежать у відповідних нормальних площинах; 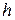– перевищення точок поверхні Землі (при відображенні поверхні еліпсоїда всі ).

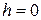З точністю до членів з 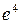отримуємо формули зв'язку полярних сфероїдичних та геодезичних систем координат:

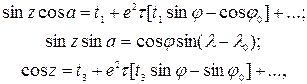
де

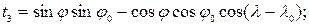
Ізометричну систему координат визначають під умовою, щоб при рівності диференціалів ізометричних широт і довгот і відповідні їм нескінченно малі дуги меридіана 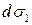і паралелей були також рівні, що має важливе значення при розробці і використанні ряду картографічних проекцій (рівнокутних).

Формула ізометричної широти точок еліпсоїда обертання має вигляд:

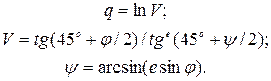
Локальні системи координат функціонально пов'язані з прямокутною системою координат карти, яка складається (моделі ГІС) і призначені для вирішення трьох основних завдань:

• введення в пам'ять ЕОМ зображення з вихідних картографічних матеріалів;

• побудови системи умовних знаків і безпосереднього математичного опису досліджуваних кривих;

• усунення (ослаблення) спотворень через деформацію паперу, з’єднання фарб для друку, помилок складання тощо.

8.2 Визначення картографічних проекцій, картографічні мережі

Дамо два визначення проекції:

1. Картографічною проекцією називається математично виражений спосіб відображення поверхні Землі або інших небесних тіл, які приймаються за еліпсоїд, сферу або інші регулярні поверхні, на площині.

2. Картографічною проекцією називається спосіб встановлення взаємо-однозначної відповідності точок поверхні, яка відображається і площини.

Зображення на картах ліній меридіанів та паралелей у прийнятій картографічній проекції називається картографічною сіткою. Частота її ліній встановлюється в залежності від призначення карти. Вид картографічної сітки залежить від рівнянь даної проекції.

8.3 Нескінченно мала сфероїдинчна трапеція

Елементами нескінченно малою сфероїдичної трапеції є (рис. 8.2):

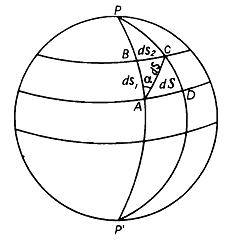
Рисунок 8.2 – Елементи сфероїдичної трапеції

– нескінченно малий відрізок меридіана;

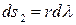– нескінченно малий відрізок паралелі;

– лінійний елемент еліпсоїда;

– азимут лінійного елемента;

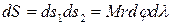– площа нескінченно малою трапеції,

де 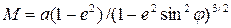– радіус кривизни меридіанного перерізу;

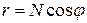– радіус кривизни паралелі.

Елементами зображення нескінченно малої сфероїдичної трапеції на площині є (рис. 8.3):

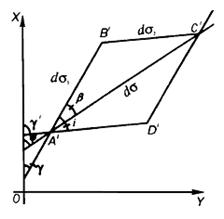
Рисунок 8.3 – Елементи зображення нескінченно малої

сфероїдичної трапеції

– лінійний елемент на площині;

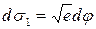– зображення на площині нескінченно малого відрізка меридіана;

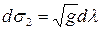– зображення на площині нескінченно малого відрізка паралелі;

– кут між зображеннями меридіанів і паралелей в точках проекції;

– відхилення кута від прямого;

– азимут лінійного елемента на проекції;

– площа зображення нескінченно малої трапеції на проекції,

де: – коефіцієнти Гауса:

8.4 Масштаби

У теорії картографічних проекцій розглядаються поняття та формули лінійних масштабів і масштабів площ. Лінійні масштаби підрозділяються на головний (розглянуто в наступній лекції) і частковий масштаби довжин. Частковим масштабом довжин відображення в даній точці за даним напрямком називається відношення нескінченно малого відрізка на проекції до відповідного нескінченно малого відрізка на поверхні еліпсоїда (сфери). Формула часткових масштабів довжин в кожній точці проекції по заданому напрямку 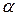має вигляд:

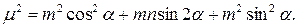
При азимутах напрямки відповідно і отримуємо:

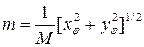– формула часткового масштабу довжин вздовж меридіанів;

– формула часткового масштабу довжин вздовж паралелей;

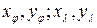– часткові або звичайні похідні прямокутних координат проекції за широтою та довготою .

Частковим масштабом площі називають відношення нескінченно малої площі на проекції до відповідного нескінченно мало площі 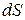на поверхні еліпсоїда (сфери).

Формули часткових масштабів площ р має вигляд:

де 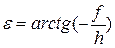– відхилення кута між зображеннями меридіанів і паралелей на проекції від прямого;

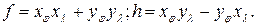
У кожній точці за двома ортогональними напрямками часткові масштаби довжин приймають екстремальні значення: 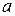– найбільший, 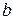– найменший часткові масштаби. Напрями, за якими часткові масштаби екстремальні називаються головними. У проекціях з ортогональною картографічною сіткою головні напрямки збігаються з напрямками меридіанів і паралелей.

Екстремальні часткові масштаби довжин визначаються за формулами:

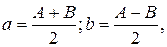
де ;

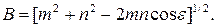
8.5 Умови відображення поверхні еліпсоїда (сфери) на площині

Картографічні проекції за характером спотворень можуть бути рівнокутні, рівновеликі та довільні (у окремих випадках еквідистанційні). При отриманні цих проекцій необхідно домогтися, щоб їх рівняння задовольняли відповідним умовам відображення.

Рівнокутними проекціями називають такі, в яких відсутні перекручування кутів і азимутів лінійних елементів, тобто в яких одночасно виконується дві умови:

- картографічні сітки цих проекцій повинні бути ортогональними;

- в кожній точці проекції, часткові масштаби довжин не повинні залежати від напрямів, за якими вони визначаються.

Ці умови мають вигляд 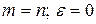або 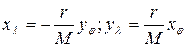(умова Коші-Рімана).

Рівновеликими проекціями називаються такі, в яких площі S і 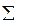зазначених областей на поверхні еліпсоїда (сфери) і на площині тотожний рівні (пропорційні). У цих проекціях повинно бути або , або .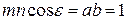

Еквідистанційними називаються проекції, що зберігають довжини по одному з головних напрямків. Найбільш часто до них відносять проекції з ортогональною картографічною сіткою, в яких зберігаються довжини або вздовж меридіанів, або вздовж паралелей.

8.6 Спотворення картографічних проекцій

Найважливішим фактором вибору та використання картографічних проекцій є величини і характер спотворень використовуваних проекцій. Їх аналіз дозволяє оцінити достоїнства розглянутих проекцій і використовувати отримані дані для вирішення ряду практичних і наукових завдань.

Зазвичай наголошується, що на картах мають місце два види спотворень:

• спотворення довжин у всіх проекціях кутів і площ (крім, відповідно, рівнокутних і рівновеликих проекцій), що виникають із-за змін часткових масштабів у точках проекцій і дають характеристику відображень в цих точках;

• спотворення в довжинах кінцевих прямолінійних відрізків і кутах між ними, а також у азимутах цих напрямків, що виникають при виконанні вимірювань на картах через кривизну зображення геодезичний ліній. Геометричну інтерпретацію спотворення дає поняття про еліпсі спотворення (рис. 8.4, 8.5).

Рисунок 8.4 – Нескінченно малі коло Рисунок 8.5 – Схема побудови

і трапеція на еліпсоїді еліпса спотворень

У загальному випадку нескінченно мале коло на поверхні еліпсоїда (сфери) зображається на площині нескінченно малим еліпсом. В окремих випадках, а саме в рівнокутних (конформних) і напівконформних проекціях, в яких часткові масштаби довжин вздовж меридіанів і паралелей рівні , нескінченно мале коло на поверхні еліпсоїда (сфери) зображається на площині подібним нескінченно малим колом.

Відзначимо, що для геометричної інтерпретації спотворень зручніше використовувати не нескінченно малі, а скінченні величини. Виходячи з цього, еліпсом спотворень або індикатриси Тіссо назвали еліпс скінченних розмірів (наприклад, при радіусі кола R = 1), відповідний отриманому на площині нескінченно малому еліпсу.

Якщо за рис. 8.4, 8.5 визначити кути і v між головними напрямками на поточні точки на еліпсоїді та площини і позначити через 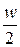найбільшу їх різницю 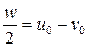, то найбільші спотворення кутів проекції визначаються формулами:

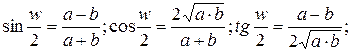
де – екстремальні часткові масштаби довжин.

Спотворення довжин на проекції характеризуються трьома показниками. Розрізняють відносні спотворення довжин в даній точці проекції з даного напрямку; відносні спотворення довжин в даній точці за всіма напрямками і середньоквадратичні (середньоарифметичні) величини спотворень в межах всієї області, яка зображується.

Міри відносних спотворень довжин в даній точці за даним напрямком приймають такі величини:

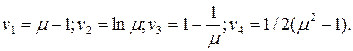
Всі ці величини різняться між собою лише малими другого або більш високих порядків малості щодо самих їх величин.

За загальну міру відносних спотворень довжин в даній точці за всіма напрямами беруть формули, запропоновані різними вченими:

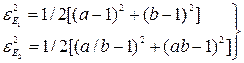– критерій Ейрі;

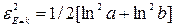– критерій Ейрі-Каврайського;

– критерій Йордану;

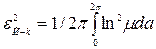– критерій Йордану-Каврайського;

– критерій Конусової, за допомогою якого оцінюється або задається характер спотворень проекцій:

– для рівнокутні проекцій;

– для рівновеликих проекцій;

- для проекцій довільних за характером спотворень.

Крім зазначених, для оцінки достоїнств картографічних проекцій були також запропоновані і використовувалися інші критерії (Клінгача, Вебера, Ейзенлора, Фролова та ін.)

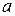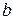Зауважимо, що для проекцій з ортогональною картографічною сіткою у всіх зазначених критеріях екстремальні часткові масштаби «» і «» приймають значення часткових масштабів довжин вздовж меридіанів m і вздовж паралелей n. Величини спотворень довжин у межах всієї області, яка зображується, оцінюються за допомогою критеріїв мінімаксного або варіаційного типів.

Критерієм мінімаксного типу є критерій П.Л. Чебишева, згідно з яким для проекції, яка досліджується, визначається відношення найбільшого значення часткового масштабу довжин 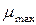до найменшого значення 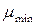. При використанні критеріїв варіаційного типу для проекції, яка розглядається, визначається значення одного з функціоналів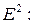

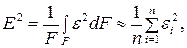
де обчислюється за одним із зазначених критеріїв і їм аналогічним.

Спотворення площ визначаються з виразу .

Рисунок 8.6 – Азимут і дирекційний кут

Слід зазначити, що при розробці проекцій, якщо домагатися усунення спотворень площ, то приблизно вдвічі збільшиться спотворення кутів і навпаки.

При виконанні вимірювання азимутів (кутів) (рис. 8.6) і довжин відрізків по карті, крім зазначених спотворень, виникає ще спотворення в азимутах (кутах) і довжинах 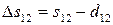через кривизну зображення на картах геодезичних ліній. Ці величини спотворень (поправок) при використанні карт, складених у рівнокутних проекціях можна визначити за формулами:

де 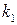– кривизна зображення розглянутої лінії в початковій (першій) точці, яка визначається за формулою:

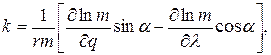
де – радіус кривизни паралелі; 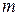– частковий масштаб довжин в першій точці; 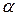– азимут напряму лінії 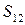; 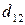– хорда лінії .

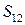Визначення величин цих спотворень, особливо при використанні нерівнокутних проекцій, представляє певні труднощі.

8.7 Методи перетворення картографічних проекцій під час створення карт геоінформаційних систем

У багатьох випадках створення карт ГІС вихідні картографічні матеріали складено в проекціях, відмінних від проекцій створюваних карт.

Виникає необхідність виконання їх перетворень і. отже, перетворення всього зображення карт. Існує два основних способи вирішення цієї задачі.

Перший передбачає попереднє визначення геодезичних координат за прямокутними координатами точок вихідного картографічного матеріалу, а потім за цими геодезичними координатами обчислення прямокутних координат карти, яка створюється (за формулами математичної картографії).

У другому способі встановлюється безпосередній зв'язок прямокутних координат проекції вихідного картографічного матеріалу та карти, яка створюється. Оскільки визначити аналітичний зв'язок цих систем координат вельми складно, для вирішення цього завдання застосовують різного виду поліноми.

Основною частиною першого способу є визначення геодезичних координат за прямокутними координатами точок вихідного картографічного матеріалу, так як обчислення прямокутних координат другої проекції за відомими формулами не викликає труднощів. Вирішення цього завдання можна виконати на основі використання ланцюжка формул, визначених для кожної проекції, або методом ітерацій, розглянутих у підручниках з математичної картографії. Цей спосіб має ряд переваг у порівнянні з другим способом, так як забезпечує високу точність перетворень і вільний від усіляких обмежень.

Другий спосіб доцільно застосовувати у випадку, коли відсутні дані о проекціях вихідного картографічного матеріалу, а також у разі перетворення малих за площею ділянок карти. У цьому способі виникають обмеження, пов'язані з відмінностями в характері спотворень розглянутих картографічних проекцій, у відмінностях у відображенні географічних полюсів і характері симетричності картографічних сіток щодо середнього меридіана і екватора. При використанні цього способу розміри малих дільниць перетворення встановлюють з розрахунку, щоб на стику цих ділянок зображення одних і тих самих контурів не перевищували 0,3-0,4 мм у масштабі карти.

8.8 Фактори і способи вибору картографічних проекцій

Вибір картографічних проекцій повинен забезпечити оптимальні умови розв'язання задач ГІС по картах. Вибір картографічних проекцій залежить від багатьох факторів, які можна розбити на три групи.

До першої віднесемо фактори, які характеризують об'єкт картографування. Це географічне положення території, яку зображують, її розміри, конфігурація, значимість окремих її частин, ступінь показу суміжних територій.

Друга група включає чинники, що характеризують карту, яку створюють. У цю групу входять зміст і призначення карти ГІС у цілому, способи та умови її використання при вирішенні задач ГІС, вимоги до точності їх вирішення.

До третьої групи віднесемо фактори, які характеризують картографічну проекцію, яку отримують (допустимі максимальні величини спотворень, характер їх розподілу, кривизна зображення ліній меридіанів, паралелей, ортодромії, локсодромії).

Вибір картографічних проекцій здійснюється у два етапи: на першому встановлюється сукупність проекцій (або їх властивостей), з яких доцільно проводити вибір, на другому – визначають шукану проекцію. Перед вибором нових проекцій визначають чи не можна у відповідності до поставлених вимог використовувати проекції, які раніше застосовувалися для аналогічних карт.

При виборі вихідної сукупності проекції прагнуть, щоб центральні лінії або точки проекцій, поблизу яких масштаби мало змінюються, знаходилися в центрі території, а центральні лінії спрямовані, по можливості, у напрямку найбільшого поширення цих територій.

Тому для багатьох карт вибирають:

• циліндричні проекції – для територій, які розташовані поблизу і симетрично відносно екватора, і витягнутих по довготі;

• конічні проекції – для тих самих територій, але не симетричних щодо екватора або розташованих у середніх широтах;

• азимутальні проекції – для зображення полярних областей.

Для двох-трьох із них, які мають найменші величини спотворень, виводять на екран монітора картографічні сітки з ізокіл (лініями рівних перекручувань) і вибирають ту з них, в якій забезпечуються найменші величини спотворень, кращий і простий вид картографічної сітки, а при рівних умовах – більш простий математичний апарат проекції.

8.9 Контрольні запитання та завдання

1. Які системи координат прийняті в ГІС?

2. Дайте визначення картографічних проекцій.

3. Дайте визначення картографічній мережі.

4. Назвіть основні елементи сфероїдичної трапеції та наведіть її зображення на площині.

5. Масштаби. Основні визначення.

6. Назвіть умови відображення поверхні еліпсоїда (сфери) на площині.

7. Які спотворення картографічних проекцій Ви можете навести?

8. Методи перетворення картографічних проекцій під час створення карт ГІС.

9. Фактори і способи вибору картографічних проекцій для створення карт ГІС.

9 Масштаби. Картографічні проекції.

План лекції: Головні масштаби, компонування та розграфлення карт, координатні сітки та номенклатури. Теорія класів і окремих варіантів картографічних проекцій. Циліндричні проекції. Псевдоциліндричні проекції. Конічні проекції. Азимутальні проекції. Перспективні азимутальні проекції. Псевдоконічні проекції. Псевдоазимутальні проекції. Поліконічні проекції. Проекції Гауса-Крюгера і UТМ. Проекція Чебишева. Проблеми вибору найкращих проекцій.

9.1 Головні масштаби, компонування та розграфлення карт, координатні сітки та номенклатури

Головний (загальний) масштаб карти, що підписується на її полях, показує у скільки разів зменшено лінійні розміри земного еліпсоїда (кулі) при його зображенні на карті. Він встановлюються до визначення картографічної проекції, зберігає свою величину тільки в окремих точках або лініях карти.

При проектуванні нової картки або серії карт вибір масштабу карти залежить від таких факторів, як територіальне охоплення території, від призначення карти, характеру її використання, теми карти, значущості зображуваної території, її географічних особливостей, найменших площ, які можуть бути зображені на карті, необхідності і можливості навантаження карти елементами загального та спеціального змісту, забезпечення складання карт матеріалами в прийнятних масштабах.

Принципово можна виділити два основних підходи до встановлення масштабу карти, що випливають з призначення карти і характеру її використання.

Перший підхід – вибір масштабу для карт, по яких передбачається виконувати картометричні роботи. Основна вимога: забезпечити задану точність вимірювань за картою.

Другий підхід, коли вимоги до точності вимірювань на карті не грають визначальної ролі. Тоді основними факторами вибору масштабу є розміри та формат карт і атласів, які створюються, у прийнятих проекціях.

Розробка масштабних рядів для конкретних систем, видів, типів карток у загальному випадку представляє дуже складну задачу. 17 липня 1934 був встановлений масштабний ряд топографічних карт СРСР: 1:10 000, 1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000 та 1:1 000 000. Одночасно були встановлені стандартні масштаби для виконання зйомок і виготовлення топографічних планів: 1:500, 1:1 000, 1:2 000, 1:5 000.

У зарубіжних країнах, по зведенню офіційних даних, яке виконано Економічною і Соціальною радою ООН, виділено чотири групи топографічних карт: перша – 1:1 250 – 1:31 680 (до неї входять масштаби 1:1 250, 1:2 500, 1:5 000, 1:10 000, 1:25 000 та ін); друга – 1:40000 – 1:75000 (1:50000); третя – 1:100000 – 1:126720; четверта – 1:140000 – 1:253000 (1:200000, 1: 250000).

При створенні дрібномасштабних карт масштабний ряд надзвичайно різноманітний.

Практичним шляхом визначено найвигідніші коефіцієнти переходу масштабів: 1:2; 1:2,5 іноді 1:3. При цьому полегшується створення карт різних масштабів на одну і ту ж саму територію.

Під компонуванням карти розуміють встановлення положення рамок карти, розміщення назви карти, її легенди, врізних (додаткових) карт і графіків щодо картографічної сітки, вирішення питань розграфлення карти, тобто її поділ на листи.

Проектування компонування залежить від багатьох факторів, до числа яких відносять:

• призначення карти, її проектоване зміст;

• картографічна проекція і головний масштаб карти, які обираються ще до початку проектування компонування карти;

• умови застосування карти (настільна, настінна, багатолисті або однолістні, в атласі або окремо, орієнтування зображення відносно півночі і т.п.),

• умови аналізу картографічної інформації (візуально, за допомогою ЕОМ чи з допомогою різних методів досліджень);

• вимоги економічної ефективності (забезпечення заданих розмірів карти та її листів, найбільш повне використання корисної площі друкарських форм при виданні і т.ін.).

Компонування по лініях картографічної сітки в основному застосовується при створенні топографічних карт. По лініях координатної сітки компоновка застосовується рідко. Прямокутне розграфування застосовується головним чином, при створенні дрібномасштабних карт і супроводжується допоміжними таблицями (схемами), в яких вказується розміщення листів. Так наприклад розграфування (нарізка) морських навігаційних карт проектується так, щоб генеральними картами (масштабу від 1:500 000 до 1:5 000 000) покривалося все море, шляховими картами (масштабу від 1:100 000 до 1:500 000) – певна смуга моря уздовж берега; частковими картами (масштабу від 1:25 000 до 1:75 000) і планами (масштабу від 1:500 до 1:25 000) – окремі райони (бухти, порти, і.т.д.).

При компонуванні атласних карт дотримується строго встановлений формат (загальні розміри всієї карти) і географічна цілісність території, зображена в межах окремих листів.

На географічних картах надається зображення із заданою частотою сітки меридіанів і паралелей, яке називається картографічною сіткою. На деяких топографічних картах замість картографічної наводиться координатна сітка (система взаємно-перпендикулярних ліній, звані так само кілометровими сітками).

Крім цих сіток або замість них на деяких картах можуть надаватися зображення інших систем ліній – спеціальних сіток, призначених для вирішення навігаційних та інших завдань.

Розграфування карт на аркуші вимагає їх позначення. Система позначень аркушів даної карти називається її номенклатурою. Основна система номенклатури – це система табличних позначень і система цифрових покажчиків. Найбільшого поширення набули табличні системи – кожен аркуш карти отримує цифрові чи літерні позначення. Така система, наприклад, прийнята в Росії для всіх топографічних і оглядово-топографічних карт.

Система цифрових покажчиків полягає в тому, що номенклатурою служать координати однієї з точок даного листа, написані в певному порядку. Номенклатура має вигляд дробу – в чисельнику вказується широта і довгота кута аркуша карти, найближчого до екватора і Гринвіцького меридіану, а в знаменнику розміри листа (без поділу градусів і хвилин).

9.2 Теорія класів і окремих варіантів картографічних проекцій

Найважливішим питанням створення і використання базових карт ГІС є вибір картографічних проекцій, що забезпечують оптимальне рішення просторових задач ГІС по картах.

Кожна картографічна проекція володіє тими чи іншими перевагами і недоліками. Їх вибір залежить від призначення карти, яка створюється, особливостей картографічної території і властивостей розглянутих проекцій.

Картографічні проекції можуть класифікуватися за різними ознаками:

• орієнтуванням картографічної сітки в залежності від положення;

• точки полюса прийнятої системи координат;

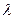• вигляду нормальної картографічної сітки ліній (= соnst, = соnst);

• вигляду загальних рівнянь картографічних проекцій;

• характером спотворень (властивостями зображення);

• способами одержання проекцій тощо.

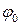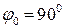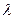Класифікація проекції за орієнтуванням картографічної сітки залежить від широти точки полюса Q системи координат, яка використовується. При полюс прийнятої системи збігається з географічним полюсом – отримуємо прямі проекції, в яких сітка меридіанів і паралелей =соnst, =соnst має найбільш простий вигляд; її називають нормальною.

При 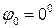– отримуємо поперечні проекції, при 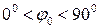– косі. У косих і поперечних проекціях нормальна сітка співпадає з сіткою вертикаль і альмукантарат (круг рівних висот), а лінії меридіанів і паралелей зображуються кривими.

Як вже зазначалось, за характером спотворень проекції поділяються на рівнокутні, рівновеликі і довільні, зокрема еквідистанційні. За виглядом нормальної картографічної сітки виділяють наступні основні класи проекцій: циліндричні; псевдоциліндричні, конічні, азимутальні, псевдоконічні, псевдоазимутальні, поліконічна проекція в широкому та вузькому сенсах. Крім того розглядають перспективні азимутальні проекції з "позитивним" зображенням – математичні моделі кадрових космічних знімків, проекції Гауса-Крюгера і UТМ – основних проекцій топографічних карт, проекцію Чебишева – найкращу рівнокутну проекцію тощо.

Коротко розглянемо основні особливості цих проекцій.

9.3 Циліндричні проекції

У циліндричних проекціях меридіани зображуються паралельними прямими, а паралелі – паралельними прямими, ортогональними меридіанам (рис. 9.1).

Рисунок 9.1 – Циліндричні проекції

Загальні рівняння циліндричних проекцій і формули часткових масштабів довжин вздовж меридіанів (т) і паралелей (n), найбільших спотворень кутів (w) мають вигляд:

де 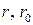– відповідно радіуси кривизни поточних паралелей і паралелі 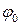=соnst, на якій немає спотворень довжин.

Ці проекції можуть бути рівнокутні (якщо т = п), рівновеликими (якщо р = тп =1) та еквідистанційні вздовж меридіанів (якщо т =1). Найбільше значення з цих проекцій має рівнокутна циліндрична проекція – проекція Меркатора (особливо для створення навігаційних і аеронавігаційних карт), в якій локсодромії (лінії, що перетинають на поверхні еліпсоїда всі меридіани під постійними кутами), зображуються прямими лініями, що істотно полегшує рішення навігаційних завдань по цих картах. Циліндричні проекції доцільно застосовувати для картографування територій, розташованих поблизу екватора, симетрично до нього і сильно витягнутих по довготі.

9.4 Псевдоциліндричні проекції

Псевдоциліндричними називаються проекції, у яких паралелі зображуються прямими лініями, а меридіани – кривими, симетричними відносно середнього прямолінійного меридіана (рис. 9.2).

Загальні рівняння цих проекцій, формули часткових масштабів довжин вздовж меридіанів (m), паралелей (n), площ (р) найбільших спотворень кутів (w) і відхилень кутів між меридіанами і паралелями на проекції від прямого мають вигляд:

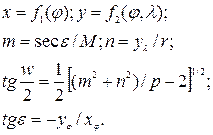
У псевдоциліндричних проекціях можна зобразити всю картографічну поверхню, а при необхідності повторити частини зображення по довготі.

Географічні полюса можна показати точками або лініями, які паралельні екватору і називаються полярними лініями.

Меридіани мають заданий вигляд, зображуються найчастіше еліпсами або синусоїдами, але можна отримати псевдоциліндричні проекції, у яких меридіани мають вигляд парабол, гіпербол та інших кривих.

Рисунок 9.2 – Рівновелика синусоїдальна

псевдоціліндріческая проекція Сансона

Ці проекції можуть бути тільки рівновеликими або довільними за характером спотворення і застосовуються, головним чином, для картографування всієї земної кулі в цілому.

9.5 Конічні проекції

Конічними називають картографічні проекції, у яких паралелі зображаються концентричними колами, а меридіани – пучком прямих, проведених з центру кіл. При цьому кути в точці полюса між меридіанами на проекції і еліпсоїді (сфері) пропорційні і, отже, на проекції в точці полюса виникає розрив зображення (рис. 9.3).

Рисунок 9.3 – Системи координат в нормальній конічної проекції

Загальні рівняння конічних проекцій і формули часткових масштабів довжин вздовж меридіанів (т) і паралелей (n), найбільших спотворень кутів (w) мають вигляд:

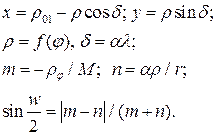
Проек

Дата добавления: 2014-01-07