Логические схемы в КА

Логические (комбинационные) схемы (ЛС или КС) – преобразователи бинарной информации, реализующие функциональное преобразование конечных множеств на базе теории двоичных булевых функций – булевой алгебре.

Функциональная схема преобразования ИП в ЛС представлена на рис.1.3.1. На этой схеме:

· А – множество элементов входной информации;

· В – множество элементов выходной информации;

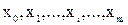· – отдельные входы ЛС для приёма кода элемента А;

· X – множество входов блока ЛС;

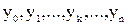· – отдельные выходы ЛС для выдачи кода элемента B;

· Y – множество выходов блока ЛС;

· F – общая функция преобразования кодов X в коды Y (X®Y).

В данном случае множества элементов входной информации А и выходной информации В имеют цифровую природу. Эти множества состоят из элементов:

А – a₀,a₁, …, a_j, …, a_L;

B – b₀, b ₁, …, b_c, …, b_V;

Элементы множеств А и В кодируются двоичными кодами:

a_j = x_0j, x_1j, …, x_ij, …, x_mj – элемент a_j входного множества А, представленный в кодированном виде вектором бинарных переменных. Здесь x_ij – значение i-ой переменной при кодировке j-го входного состояния.

b_j = y_0j, y_1j, …, y_kj, …, y_nj – элемент b_i выходного множества B, представленный в кодированном виде вектором бинарных переменных. Здесь y_kj – значение k-ой переменной при кодировке j-го выходного состояния.

Входные состояния однозначно преобразуются в выходные, т.е. каждому входному состоянию всегда соответствует одно и то же выходное состояние, поэтому индекс j указан одинаковый. Хотя в принципе выходных состояний может быть меньше, чем входных (нескольким входным будет соответствовать одно и то же выходное состояние). НО! Выходных состояний не может быть больше, чем входных.

Число двоичных векторов длины n равно 2ⁿ.

т.е. имея n переменных невозможно закодировать количество состояний, большее, чем 2ⁿ.

Обычно количество, как входных, так и выходных шин превышает минимально необходимое значение, т.е. длина входных/выходных векторов может быть избыточной.

Обратно, если количество состояний равно S, то

► Минимальная длина вектора, кодирующая S состояний равна
M = [log₂S], ●

здесь 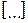– округление в большую сторону до ближайшего целого числа (см. таблицу рис.1.3.4).

Если длина входного вектора превышает минимальную, то в выходном векторе некоторые значения при кодировании устанавливаются неопределёнными.

Пусть m и n –длины двоичных векторов для кодирования состояний входных и выходных множеств А и В. Тогда кодирование – это построение отображения A®{0,1}^m, построение отображения {0,1}ⁿ®B, а функциональное отображение F сопоставляет каждому вектору из {0,1}^m определённый вектор из {0,1}ⁿ.

Дата добавления: 2014-01-07