Пример. Пусть входное множество имеет пять состояний A ={ a0, a1, a2, a3, a4}, а выходное множество имеет три состояния B={ b0

Пусть входное множество имеет пять состояний A ={ a₀, a₁, a₂, a₃, a₄}, а выходное множество имеет три состояния B={ b₀, b₁, b₂}. Отображение F задаётся таблицей рис.1.3.5. В данном примере длина входного вектора не менее трёх, а выходного не менее двух.

Произвольно выберем функцию кодирования (рис.1.3.6 а) и декодирования (рис.1.3.6 б) отображение F строим в соответствии с таблицей отображения рис.1.3.5 (рис.1.3.6 в).

Проблема построения произвольного преобразователя F:{0,1}^m®{0,1}ⁿ довольно сложна. Для упрощения этой проблемы используют простой приём: вместо одной функции F:{0,1}^m®{0,1}ⁿ строится n одноразрядных по выходу функций f_i:{0,1}^m®{0,1} так, чтобы реализация этих функций дала искомый преобразователь F. Структура ЛС с явно выделенными f_i представлена на рис.1.3.2. Для удобства чтения схем используются шины, в которых объединяются некоторые соединения, а входы и выходы соединений в шину именуются. Шинная организация структуры ЛС показана на рис.1.3.3.

► Функции вида f_i:{0,1}^m®{0,1}, сопоставляющие двоичным векторам одноразрядные двоичные значения, называются двоичными (или булевыми) функциями.●

Булевы функции определены на конечном множестве аргументов, каждый из которых принимает только два значения, 0 или 1. Булевы функции представляются таблицей, перечисляющей для каждого набора значений входных аргументов значение функции. Для булевых функций разработаны методики эффективной обработки. Представление таблиц примера через булевы функции показано на рис.1.3.7.

Выделенная часть таблицы (прямой шрифт) может быть реализована совокупностью ЛС (рис.1.3.8.а). Каждый блок ЛС реализует свою БФ (f₀, f₁). Выходы блоков ЛС представляют собой физическую реализацию булевых переменных и выражаются, как

, .

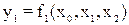Выделенную часть таблицы рис.1.3.7 называют таблицей истинности (ТИ). Но с учётом того, что ЛС имеют выходами булевы переменные, таблицу истинности обычно представляют в виде, показанном на рис.1.3.8.б (но можно и как в 1.3.7).

В ТИ в строках указываются:

· в левой части – все возможные состояния входных переменных
(x₀, x₁,x₂),

· в правой части – состояния выходных переменных (y₀, y₁) после преобразования БФ входных переменных данной строки.

Если по тем или иным причинам состояние выходной булевой переменной в строке безразлично (т.е. может принимать значение как 0, так и 1), то для данной выходной переменной в строке проставляется прочерк.

Для сокращения размеров структурных схем допускается представление структуры рис.1.3.8.а в виде рис. 1.3.8.в. Просто надо помнить, что каждая выходная переменная реализуется своей БФ.

Длина ТИ определяется 4количеством входных переменных. Для n входных переменных длина M таблицы составляет

M = 2ⁿ.

Максимальное количество ТИ длиной M от n переменных составляет

N = 2^M = .

► Таблица истинности – алгоритм работы логической схемы.●

16 час.

Дата добавления: 2014-01-07