Булевы функции

Основной задачей теории булевых функций (БФ) является разработка систематических методов построения сложных функций из более простых. Булевых функций от заданного числа m двоичных переменных – конечное число. Изучим свойства булевых функций.

Рассмотрим все возможные БФ от одной переменной. Этих функций четыре:

· константа нуля;

· константа единицы;

· тождественная функция;

· функция отрицания (функция НЕ).

Представляя эти функции в табличном виде, получим ТИ, представленные на рис. 1.4.1. С целью сокращения текста в одной таблице можно отражать несколько БФ от одного и того же сочетания переменных. Объединённая таблица истинности БФ от одной переменной представлена на рис.1.4.2.

Основные БФ от двух переменных представлены в объединённой ТИ рис.1.4.3. На рисунке приведены функции:

1. f₀ = – инверсия p.

2. f₁ = – инверсия q.

3. f₂ = 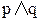– функция И (конъюнкция). Можно писать f₂ = .

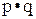4. f₃ = 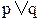– функция ИЛИ (дизъюнкция).

5. f₄ = 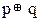– функция сложения по модулю 2 (eXclusive OR – XOR).

6. f₅ = p – тождественна p.

7. f₆ = q – тождественна q.

8. f₇ = 0 – константа 0.

9. f₈ = 1 – константа 1.

10. f₉ = 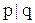– штрих Шеффера (операция Шеффера). f₉ = 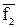– И-НЕ.

11. f₁₀ = 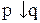– стрелка Пирса. f₁₀ = – ИЛИ-НЕ.

12. f₁₁ = 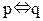– функция эквивалентности. f₁₁ = .

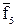13. f₁₂ = 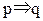– импликация или функция логического следования.

С нулевой по восьмую БФ являются основными все остальные функции можно выразить через их суперпозицию (т.е. различного рода их сочетания) в виде логического выражения (логической формулы).

► Логическое выражение ­– символьная формула, представляющая собой суперпозицию двоичных (булевых) функций.●

Например, логическая формула

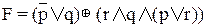
или, перепишем это же выражение с другим обозначением операции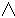

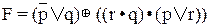
задаёт функцию от трёх переменных как суперпозицию функций от одной и двух переменных.

Логическое выражение даёт возможность построить соответствующий функциональный преобразователь, если имеются «базисные» преобразователи. Для реализации преобразователя F примера необходимо иметь элементы, реализующие отрицание, дизъюнкцию, конъюнкцию и сложение по модулю два. Синтаксическая структура формулы примера показана на рис. 1.4.4. Табличное представление суперпозиции функции F показано на рис 1.4.5.

Примечание. Реализацию БФ в виде ЛС на логических элементах (рассматривается в дальнейшем) следует начинать «сверху - вниз» от выхода к входам. Так на рис.1.4.4 сначала реализуется сумма по модулю два и т.д. На последний уровень подаются входные сигналы (входные переменные).

Для уменьшения числа скобок вводятся приоритеты операций:

· отрицание – высший приоритет;

· конъюнкция ­– второй приоритет;

· дизъюнкция

С остальными функциями проблемы с приоритетами.

► Желаемый порядок выполнения операций можно установить скобками.●

При возникновении сомнений в порядке выполнения операций лучше всего в выражении использовать скобки.

Суперпозицией фиксированного набора функций можно представить любую БФ от любого количества переменных.

► Любая БФ может быть представлена как суперпозиция следующих наборов двоичных функций:

· И, ИЛИ, НЕ – базис Буля;

· И-НЕ;

· ИЛИ-НЕ.

Каждый из этих наборов функций называется полным базисом. ●

►Функционально полный базис – множество двоичных функций, суперпозицией которых могут быть выражены любые БФ●

16+6=22 час.

Дата добавления: 2014-01-07