Диаграммы Вейча от двух переменных

Диаграммы Вейча

Рассмотрим минимизацию с использованием ДВ.

ДВ представляет собой прямоугольную таблицу, количество клеток (M) которой зависит от количества входных переменных БФ (n) и равно:

.

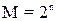Для n=1 минимизация тривиальна, поэтому рассмотрим минимизацию БФ, начиная с двух переменных.

На рис.1.8.2.а показан общий вид диаграммы Вейча, а на рис 1.8.2.б нумерованные поля диаграммы:

1. Поле для указания имени минимизируемой БФ;

2. Именованные поля первой входной переменной для прямого и инверсного состояния;

3. Именованные поля второй входной переменной;

4. Поля для заполнения значений БФ, соответствующих состояниям входных переменных.

На рис. 1.8.в выделена область, соответствующая полям заполнения в которую вносятся соответствующие значения БФ из ТИ. Для того, чтобы найти клетку для внесения значения из ТИ следует определить положение значения БФ в области заполнения (рис.1.8.2.в). Для этого область заполнения разделена на области p, , q, 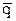, видимые на рис 1.8.2.г-ж. Так, следует проставить единицы в клетках области заполнения, если БФ принимает единичное значение для комбинаций входных переменных:

o – в клетке 0 – на пересечении областей и ;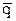

o – в клетке 1 – на пересечении областей и q;

o – в клетке 2 – на пересечении областей p и ;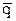

o – в клетке 3 – на пересечении областей p и q.

Рассмотрим заполнение диаграмм Вейча на примере некоторых БФ, заданных ТИ (рис.1.8.3) в соответствии с последовательностью действий:

· Определить для каждой строки ТИ вид конституенты. Для этого написать последовательность всех входных переменных и проставить инверсии над переменными, имеющими в данной строке ТИ значение нуля.

· Последовательно выделить области, соответствующие значению каждой входной переменной.

· На пересечении выделенных областей проставить значение БФ.

Рассмотрим заполнение диаграммы Вейча для БФ f₀:

· Выбираем нулевую строку ТИ. Для этой строки входные переменные принимают значения p = 0 и q = 0. Соответственно конституента имеет вид .

· Выделяем области и .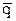

· Определяем, что пересечением областей буде клетка 0 (рис.1.8.2.в).

· Значение БФ равно 0, проставляем 0 в найденную клетку.

· Аналогично поступаем для остальных клеток ТИ:

o – в клетке 1 – на пересечении областей и q – 0;

o – в клетке 2 – на пересечении областей p и 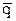– 1;

o – в клетке 3 – на пересечении областей p и q – 1.

Самостоятельно рассмотрите заполнение диаграмм Вейча для БФ f₁-f₅. БФ f₆ диаграмму Вейча заполненную одними единицами.

Для минимизации необходимо выполнить накрытия единичных клеток диаграммы прямоугольниками, имеющими площадь, равную целой степени двух, т.е. для БФ от двух переменных можно накрывать одну, 2 или 4 клетки.

Одну и ту же клетку можно накрывать сколько угодно раз.

Необходимо стремиться, чтобы накрытия имели как можно большую площадь, так для БФ f₆ будут накрыты все четыре клетки.

Минимизация БФ основывается на многократном применении свойства БФ – склеивании.

Так для функций примера f₀, f₃ и f₆:

· ;

·

;

· .

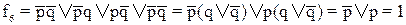Подобные вычисления для диаграмм Вейча не делаются. Минимизация выполняется непосредственно при исследовании каждого накрытия в соответствии с последовательностью действий:

· последовательно выбираются все накрытия в диаграмме;

· в выбранном накрытии исследуются изменения областей каждой входной переменной и формируется очередная импликанта;

· если накрытие располагается только в одной области, то имя области отражается в импликанте;

· если накрытие располагается в двух областях переменной, то переменная исчезает из импликанты;

· все импликанты собираются в минимизированной БФ через ИЛИ.

Рассмотрим БФ примеров рис. 1.8.3:

· Накрытие БФ f₀ проходит через области 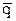и q поэтому переменная q не входит в импликанту, Это накрытие расположено в области p, не изатрагивая область поэтому в импликанту входит p. Диаграмма f₀ имеет одно накрытие поэтому минимизированная БФ f₀=p.

· БФ f₃ имеет два накрытия:

o первое – 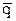-(p, ) – p исчезает (склеивается) – остаётся ,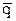

o второе – p-(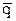, q) – q исчезает – остаётся p.

o собираем по ИЛИ импликанты и получаем минимизированную БФ:

.

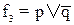· БФ f₆ пересекает все области f₆=1.

34+4=38 час

1.8.2.2. Диаграммы Вейча от трёх переменных

Диаграмма Вейча на три переменных имеет вид, показанный на рис. 1.8.4, на котором показаны:

· а – общий вид диаграммы Вейча на три переменных с выделенной областью заполнения;

· б – выделенная область переменной х₀, не выделенная часть области заполнения соответствует ;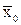

· в – выделенная область переменной х₁;

· г – выделенная область переменной х_2.

На рисунке показано, левый и правый края диаграммы являются соседними, т.е. диаграмма представляет собой кольцо.

Заполнение диаграммы производится аналогично заполнению диаграммы Вейча от двух переменных:

· из строки ТИ формируется конституента;

· отыскивается клетка, соответствующая пересечению областей переменных;

· в клетку проставляется значение БФ.

Накрытие осуществляется минимальным количеством прямоугольников максимальной площади, равной целой степени двух.

Примеры минимизации БФ f₀–f₃ показаны на рис. 1.8.5.

38+2=40 час

1.8.2.3. Диаграммы Вейча от четырёх переменных

Диаграммы Вейча для БФ от четырёх переменных аналогичным образом заполняются из ТИ БФ с использованием конституент единиц посредством установки единиц в, соответствующие пересечению областей, клетки поля заполнения. Диаграмма Вейча для БФ от четырёх переменных образно можно представить в виде тора, т.к. соседними являются клетки:

· верхнего и нижнего рядов;

· правого и левого столбцов.

Минимизация БФ традиционно выполняется с использованием четырёхугольных накрытий, максимальной площади, равной целой степени двух. Импликанты, соответствующие накрытиям собираются через «ИЛИ».

Заполнение диаграмм тривиально, поэтому рассмотрим минимизацию БФ на примерах уже заполненных диаграмм (рис.1.8.6).

Дата добавления: 2014-01-07