Карты Карно

Сложность работы с диаграммами Вейча заключается в необходимости промежуточного формирования из кода строки ТИ конституенты, а затем определения клетки диаграммы, соответствующей пересечению областей. В этом отношении карты Карно более формализованы, в следствии чего, заполнение их выполняется значительно проще. Это позволяет избежать множества ошибок при определении клетки пересечения областей существования переменной из конституенты единицы. В остальном диаграммы Вейча и карты Карно практически совпадают.

В картах Карно области существования переменных представлены в кодированном виде. Соответствие карты Карно и диаграммы Вейча для четырёх переменных показано на рис.1.8.7. Здесь области действия значений переменных указаны скобками и приведены колированные значения областей:

· в верхней строке карты показаны кодированные значения переменных x₁ и x₀:

o столбцы 0 0 и 0 1 – область действия ,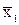

o столбцы 1 1 и 1 0 – область действия ,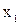

o столбцы 0 0 и 1 0 – область действия ,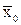

o столбцы 0 1 и 1 1 – область действия ;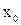

· в правом столбце карты показаны кодированные значения переменных x₃ и x₂:

o строка 0 0 и 0 1 – область действия ,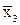

o строка 1 1 и 1 0 – область действия ,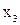

o строка 0 0 и 1 0 – область действия ,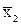

o строка 0 1 и 1 1 – область действия ;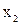

Кодировка областей существования переменных выполняется в коде Грея, характеризующемся тем, что каждая соседняя пара кодов отличается инверсией только одного разряда.

На рис.1.8.7.б приведены эквиваленты клеток и конституент (в левом столбце даны шестнадцатиричные значения кодов клеток).

40+7=47 час

Заполняется карта Карно из ТИ БФ. При заполнении карты в ТИ берётся очередная строка и минуя преобразование в конституенту производится установка значения в соответствующую клетку карты.

Рассмотрим в качестве примера минимизацию БФ f₀–f₄. ТИ этих БФ приведена на рис.1.8.8.а, а минимизация показана на рис.1.8.8.б-е. Определение склеивания какой либо переменной в минимизированной БФ производится при анализе поведения этой переменной. Если при анализе обнаружено, что накрытая область проходит и через единичное и через нулевое значение переменной, то переменная в минимизированной БФ склеивается (исчезает).

Накрытия следует выполнять:

· для всех единиц;

· одну и ту же единицу можно накрывать произвольное количество раз;

· площади накрытий должны быть максимальными и равными целой степени двух.

Карты Карно практически применимы для БФ, количество переменных которых не более шести. На рис.1.8.9. показаны карты Карно для различного количества входных переменных БФ. Для построения БФ от большего количества переменных следует либо использовать постоянные запоминающие устройства (ПЗУ), либо применять методики понижения порядка (уменьшения числа переменных) БФ.

На рис.1.8.9 под латинскими буквами подразумеваются единичные значения некоторых БФ и выполнена минимизация этих функций. Видно, что для БФ от пяти и шести переменных код Грея, записанный в рамках представляет собой зеркальное отражение.

Для контроля правильности минимизации следует использовать правило:

► Если площадь накрытия составляет N клеток то в минимизированной импликанте, относительно исходного количества переменных БФ, должно исчезнуть 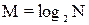переменных●

Например, для БФ от 6 переменных при накрытии 8 клеток исчезнет 3 переменных, а останется 3, при накрытии 16 клеток исчезнет 4, а останется 2. Поэтому, если при накрытии 32-х клеток вы обнаружили, что какая-то переменная для этого накрытия не меняется, то выписываем её, а остальные нет смысла и проверять. Но, если накрыто 8 клеток, а импликанта содержит четыре переменных, то одна переменная явно пропущена (д.б. пять!).

При формировании накрытия для 5, или 6 переменных, если накрытия располагаются в нескольких квадрантах, то накрытие должно быть симметрично относительно квадрантов. Например, для БФ от пяти переменных при формировании накрытия в 8 клеток, располагаемого в двух квадрантах, в каждом квадранте должно располагаться по четыре клетки, а не 2 и 6.

47+3=50 час

1.8.4. Минимизация не полностью определённых БФ

При формировании ТИ БФ вследствие объективных причин может получиться так, сто в некоторых строках значение БФ будет не определено. Этих причин может быть множество и вы сами убедитесь в этом в дальнейшем.

Рассмотрим пример рис 1.8.10. Пусть входные воздействия на ЛС формируются с выхода другой входной ЛС (ВЛС) (рис.1.8.10.а), а зависимости БФ выхода ВЛС x_i(p,q) имеют вид показанный на рис.1.8.10.б. Тогда реализация ВЛС имеет вид показанный на рис.1.8.10.в. ТИ, соответствующая заданным зависимостям показана на рис.1.8.10.г, на котором видно, что БФ ВЛС принимают только четыре значения. Вследствие этого ТИ ЛС, представленная на рис.1.8.10.д, имеет определёнными только четыре строки выделенные в колонках (x₀, x₁, x₂). Значения (x₀, x₁, x₂) в колонках, выделенных курсивом, не могут существовать в принципе, поэтому в этих строках выходы БФ (y₀, y₁) не определены и там проставлен прочерк. Предположим, что в выделенных колонках (y₀, y₁) принимают значения показанные в ТИ (рис.1.8.10.д).

► Неопределённые значения БФ при минимизации можно доопределять произвольным образом, как нулём, так и единицей с целю получения наиболее минимизированного выражения БФ.●

Доопределение выполняется непосредственно в карте Карно так, чтобы получить минимальное количество накрытий максимальной площади.

Накрытие с оптимальным доопределением показано на рис.1.8.10.е. Там же приведены минимизированные выражения БФ ЛС, которые имеют более простой вид, чем при доопределении всех неопределённых значений нулями.

Дата добавления: 2014-01-07