Уравнение Фрейндлиха, графическое определение констант адсорбции

Адсорбция газов и жидкостей на поверхности твердого тела описывается также уравнением Фрейндлиха, которое имеет следующий вид:

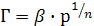
(19.5)

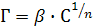
где р – равновесное давление;

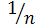с – равновесная концентрация;

b и – константы.

На изотерме Фрейндлиха нет зоны насыщения. Уравнение применимо только для малых и средних концентраций, в области высоких концентраций и давлений ононе применимо.

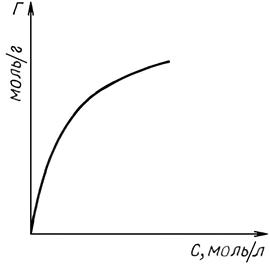
Рис. 19.2 Изотерма адсорбции Фрейндлиха

Для адсорбции из растворов уравнение Фрейндлиха как правило имеет такой вид:

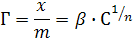
(19.6)

где С – равновесная концентрация, моль/л.

В последнем уравнении константа β обычно колеблется в широких пределах. Физический смысл константы становится ясен, когда примем С=1 моль/л. Тогда константа β представляет величину адсорбции при равновесной концентрации адсорбтива, равной 1 моль/л. Показатель 1/n – правильная дробь, характеризует степень приближения изотермы к прямой. С повышением температуры величина коэффициента β должна падать, а 1/n – возрастать.

Константы уравнения Фрейндлиха легко находятся графическим способом после его логарифмирования:

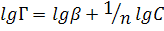(19.7)

На графике, построенном в координатах lgГ =f(lgC), отрезок, отсекаемый прямой на оси ординат, равен lgβ, а тангенс угла наклона α прямой к оси абсцисс равен 1/n.

Уравнение Фрейндлиха является эмпирическим уравнением. Кроме того это уравнение, представляющее собой уравнение параболы, не может дать прямолинейного нарастания адсорбции от равновесной концентрации, а также предельного значения адсорбции, не зависящего от концентрации. Очевидно, что прямолинейный участок (с малыми с и р) может быть получен с помощью уравнения Фрейндлиха если 1/n принять равным 1. Точно также прямолинейный участок, отвечающий высоким давлениям или концентрациям, может быть получен, если принять 1/n =0. Таким образом, коэффициент 1/n по существу должен являться сам функцией р или с. Поскольку коэффициент 1/n принимается как const, считают, что он изменяется в пределах 0,2 – 1 для адсорбции из газовой среды и 0,1 – 0,5 для адсорбции из растворов.

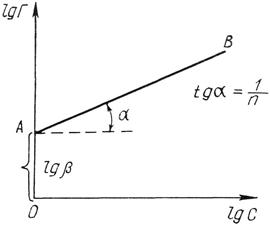
Рис. 19.3 Логарифмическая форма изотермы адсорбции Фрейндлиха

Опытные данные показывают, что в области малых и средних концентраций и давлений уравнение Фрейндлиха иногда применять удобнее, чем уравнение Ленгмюра. Поэтому его часто используют для практических целей.

Дата добавления: 2014-01-07