Лекция 12. Описание процесса проведения эксперимента

Описание процесса проведения эксперимента.

В методике подробно проектируется сам процесс проведения эксперимента. Составляют очерёдность, последовательность проведения операций измерений и наблюдений. Затем тщательно описывают каждую операцию в отдельности с учётом выбранных средств для проведения эксперимента. Разрабатывают формы журналов для записи результатов наблюдений и измерений.

Ведение журнала.

Ведение журнала является обязательным требованием проведения эксперимента. В журнале отмечают тему эксперимента, фамилию исполнителя, время и место проведения эксперимента, характеристику окружающей среды, данные об объекте эксперимента и средствах измерения, результаты наблюдений, а также другие данные дл оценки получаемых результатов.

При проведении эксперимента нужно постоянно следить за средствами измерений, систематически проводить рабочую поверку приборов.

Обоснование способов обработки и анализа экспериментальных данных.

Одновременно с производством измерений нужно проводить предварительную обработку результатов и их анализ. В этом случае можно контролировать исследуемый процесс, улучшать методику и повышать эффективность эксперимента.

Результаты должны быть сведены в удобочитаемые формы записи – таблицы, формулы, графики, номограммы,, которые позволяют быстро сопоставить полученные результаты.

Тщательно изучают сомнительные цифры, резко отличающиеся от статистического ряда наблюдений, от средних значений. При анализе цифр необходимо установить точность, с которой нужно производить обработку опытных данных.

Табличные данные не дают чёткой наглядной характеристики изучаемых процессов. Графическое изображение более наглядно позволяет выявить общий характер функциональной зависимости изучаемых переменных, установить наличие максимума и минимума функции.

Для графиков обычно используют систему прямоугольных координат.

Точки на графике необходимо соединить плавной линией.

Резкое искривление графика объясняется погрешностями измерений.

Иногда при построении графика одна-две точки резко удаляются от кривой. Вначале нужно проанализировать физическую сущность явления и если нет основания полагать наличие скачка функции, то такое резкое отклонение можно объяснить грубой ошибкой. В таких случаях необходимо повторить измерение в диапазоне резкого изменения точки.

Графики использую как материал для дальнейших расчётов, с них считывают необходимые данные. Поэтому стоит вопрос, как выбрать масштаб построения графиков и диаграмм, чтобы считывание не давало значительной ошибки.

Существует правило: чтобы наименьшее деление шкалы бумаги соответствовало вероятной ошибке измеряемой величины.

Вероятная ошибка в определении переменной «y» составляет примерно 0,01. Поэтому только средний масштаб может обеспечить необходимую точность считывания.

Координатные сетки бывают равномерными и неравномерными (логарифмическими).

При обработке результатов эксперимента применяют кроме графических, статистические методы. Главным образом, это методы статистической обработки большого количества данных измерений или наблюдений, а также методы определения ошибок измерений. Они показывают достоверность полученных данных (это математическое ожидание, дисперсия, корреляционные связи и т.д.)

Помимо статистических, в классическом эксперименте широко используют математические методы для вывода из экспериментальных данных эмпирических формул.

Конкретную эмпирическую кривую можно описать с помощью формул (алгебраическое выражение, объединяющее функцию с переменными y=f(x)). Эмпирические формулы являются приближенными выражениями аналитических формул.

Существует правило подбора эмпирических формул:

1. Строят кривую зависимости и ориентировочно выбирают вид формулы.

2. Вычисляют параметры формулы. Результаты измерений многих явлений и процессов аппроксимируются простейшими уравнениями типа y=a+bx; y=ax^b, где a и b – постоянные коэффициенты. При анализе графического материала необходимо, по возможности, использовать линейную функцию. Для определения параметров формулы a и b применяют метод выравнивания. Он заключается в том, что кривую, построенную по экспериментальным точкам, представляют линейной функцией.

3. Для преобразования некоторой кривой y=f(x) (1) в прямую линию вводят новые переменные X и Y, т.е. X=f₁(x,y); Y=f₂(x,y) (2).

В этом уравнении X и Y должны быть связаны линейной зависимостью

Y=a+bx (3).

Значения X и Y можно вычислить на основе решения системы (1). Далее строят прямую, по которой легко графически вычислить параметры a и b.

Таким образом, аппроксимация экспериментальных данных прямолинейными функциями, позволяет просто и быстро установить вид эмпирической формулы. Кроме графического метода выравнивания, для определения коэффициентов a и b применяют метод наименьших квадратов.

;

,

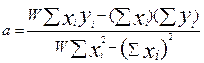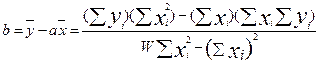где y_{i –} экспериментальное значение, соответствующее x_i.

W – число точек измерения.

Графический метод выравнивания можно применять и в тех случаях, когда кривая имеет вид плавной кривой.

Здесь кривую можно описать формулой y=ax^b. Экспериментальную кривую можно превратить в прямую на логарифмической сетке.

1. Логарифмируем уравнение y=ax^b

lg y=lg a+b*lg x

2. Заменяем lg x на X, lg y на Y и получаем уравнение прямой Y=lg a+bx.

3. Далее поступаем также, как описано для нахождения коэффициентов a и b в уравнении прямой, используя знания математики.

Дата добавления: 2014-01-07