
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы постановки задач параметрической оптимизации
|
|
|
|
Классификация критериев оптимальности.
Основная проблема постановки экстремальных задач — формулировка целевой функции. Казалось бы, здесь не следует ожидать трудностей, так как количественное выражение качества проектируемого объекта уже имеется — это вектор выходных параметров Y. Однако все выходные параметры являются функциями вектора внутренних параметров X и, следовательно, не могут изменяться независимо друг от друга. Среди выходных параметров всегда можно найти пары таких параметров, что улучшение одного из них приводит к ухудшению другого. Такие параметры называют конфликтными параметрам и.
Поэтому при оптимизации невозможно улучшение всех выходных
параметров одновременно.
Целевая функция должна быть одна и необходим переход от век
тора Y(X) к скалярной функции качества F(X). Такой переход называют свертыванием векторного критерия.
Первоначальный векторный характер критериев оптимальности
в задачах проектирования или, как часто говорят, многокритериаль-
ность задач проектирования и обусловливает сложность проблемы
постановки задач оптимизации.
В случаях, когда среди выходных параметров можно выделить параметр, наиболее важный и наиболее полно характеризующим свойства объекта, этот выходной параметр естественно и принять за целевую функцию. Такой выбор целевой функции лежит в основе критериев оптимальности, называемых частными критериями. Но в большинстве случаев отдать предпочтение какому-то одному параметру среди качественно разнородных величин довольном трудно и нужно прибегать к построению комплексного критерия, при котором целевая функция тем или иным способом объединяет все или большинство выходных параметров. Такие критерии иногда называют также обобщенными или глобальными критериями.
В зависимости от того, каким образом объединяются выходные параметры в скалярной функции качества, различают критерий мультипликативные, аддитивные, минимаксные (максиминные) и т.п. Минимаксные критерии, обладающие рядом специфических свойств, целесообразно выделить в отдельную группу.
При формулировке комплексных критериев возникает задача пре-, образования выходных параметров в некоторые безразмерные величины, сравнимые между собой. Такое преобразование, иначе нормирование, означает, что устанавливаются отношения важности выходных параметров. Количественно важность выходного параметра уj может оцениваться коэффициентом влияния уj на целевую функцию F(X). Для установления относительной важности выходных параметров в комплексных критериях инженер, должен располагать какими-либо ориентирами. В задачах проектирования наилучшим, а, часто и единственно корректным, является выбор относительной важности параметров с точки зрения степени выполнения ТЗ. Ориентация на ТЗ при формулировке комплексного критерия — один из важных принципов оптимизации в задачах проектирования. Иногда используют иные принципы, такие, как ориентация на мнение экспертов. Применение этого принципа может быть оправдано только в условиях отсутствия достаточно четко сформулированного и полного ТЗ, т. е. в случаях, когда собственно задача оптимизации объекта и задача формулировки ТЗ почему-либо решаются совместно. Если оптимизация ведется без учета статистического разброса параметров, то соответствующий критерий оптимальности называют детерминиpованным критерием, если разброс пара метров учитывается, то имеем критерий статистический.
Статистические критерии оптимальности более полно отражают представления о качестве объектов проектирования, однако их использование, как правило, ведет к заметному увеличению затрат машинного времени. Поэтому чаще используют детерминированные критерии. Рассмотрим наиболее часто встречающиеся на практике способы постановки задач оптимизации. Частные критерии. В большинстве частных критериев в качестве целевой функции принимают один из выходных параметров yk(X), все остальные выходные параметры в виде соответствующих условий работоспособности относят к ограничениям. Тогда задача становится типичной задачей нелинейного программирования: max yk (X), где ХР — область, задаваемая прямыми ограничениями на управляемые параметры и условиями работоспособности, которые могут иметь вид неравенств уj< ТТj и равенств у j — ТТ j.
Применение частных критериев в ряде случаев дает результаты, которые с физической точки зрения наилучшими назвать нельзя. Действительно, здесь можно получить большой запас по сравнению с заданным техническим требованием TTh для одного выходного параметра yk, но ряд других выходных параметров, вообще не будет иметь запасов. Несмотря на этот недостаток, частные критерии довольно широко используют в различных областях техники.
Имеются случаи, когда условия работоспособности задаются не на отдельные выходные параметры, а на характеристики — зависимости тех или иных параметров от какого-либо внешнего параметра, времени или частоты. Примерами таких характеристик могут быть амплитудно-частотная характеристика усилителя — зависимость его коэффициента усиления от частоты входного сигнала, распределение напряжения в раме автомобиля при заданных внешних условиях и т. п. При этом в ТЗ указывают желаемый вид характеристики. Использование частного критерия при оптимизации в подобных случаях вводится к замене характеристики на конечное число узловых точек и к выбору следующей целевой функции, подлежащей минимизации:
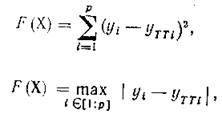 (14)
(14)
(15)
где уi и уТТi — i -e ординаты соответственно реальной и заданной характеристик; р — количество узловых точек.
Параметр yi можно рассматривать как i-й выходной параметр. И хотя в целевой функции F(X) учитывается несколько выходных параметров уi критерии (14) и (15) максимальной близости резальной и заданной характеристик остаются частными, так как условия работоспособности всех остальных выходных параметров должны 



 быть отнесены к ограничениям задачи. Учет других параметров в F(X) не может быть сделан столь же просто, как ординат характеристики, из-за Неодинаковой природы этих параметров.
быть отнесены к ограничениям задачи. Учет других параметров в F(X) не может быть сделан столь же просто, как ординат характеристики, из-за Неодинаковой природы этих параметров.
Мультипликативные критерии. Разделим выходные параметры объекта на три группы по типу соответствующих им условий работоспособности. К первой группе отнесем параметры у j+, имеющие условия работоспособности вида (16) у j+>TTj, т. е. параметры, для которых желательно максимальное увеличение. Вторую группу составят параметры уj- с условиями работоспособности вида
уj-<ТТi (17)
для них желательна минимизация.
Третья группа будет образована параметрами yk= с условиями работоспособности типа равенств
yk== TTk±Δyk, (18)
где Δyk — максимально допустимое по ТЗ отклонение yk= от ТТk. Мультипликативные критерии могут применяться в случаях, когда в ТЗ отсутствуют условия работоспособности типа равенства и выходные параметры не могут принимать нулевые значения. Тогда целевая функция, подлежащая максимизации, имеет вид
 (19)
(19)
где в числителе перемножаются все выходные параметры с условиями работоспособности типа (16), а в знаменателе фигурируют все параметры с условиями работоспособности типа (17).
Удобство этого критерия в том, что выходные параметры не требуют какого-либо нормирования. Однако, последнее приводит к следующему серьезному недостатку.
Аддитивные критерии. В аддитивных критериях целевая функция образуется путем сложения преобразованных выходных параметров. Преобразование параметров — переход к безразмерным слагаемым — необходимо и чаще всего осуществляется с помощью введения нормирующих множителей — весовых коэффициентов. Минимизируемая целевая функция может быть представлена в виде
 (20)
(20)
При этом по-прежнему предполагается отсутствие выходных параметров с условиями работоспособности типа равенств. Для большей краткости записи. Преобразуем условия работоспособности типа (16) в условиях работоспособности типа (17), что потребует умножения у j+ и соответствующих им технических требований ТТj на —1. Тогда получим единую группу выходных параметров и (20) можно записать в виде
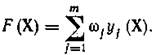 (21)
(21)
Целевая функция (21) имеет тот же существенный недостаток, что и целевая функция (19) в мультипликативном критерии, — неучет конкретных требований ТЗ в коэффициентах влияния уj(Х) на F(X). Здесь абсолютные коэффициенты влияния
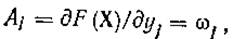
определяются выбранными весовыми коэффициентами. Обычно wj выбираются либо самим инженером, либо рекомендуются группой экспертов и в процессе оптимизации остаются постоянными.
Аддитивные критерии успешно применяют в ситуациях, когда все или основные условия работоспособности имеют вид равенств (18). Тогда целевая функция формируется как сумма квадратов уклонений у j от ТТ j с весовыми коэффициентами wj
 (22)
(22)
и оптимизация сводится к ее минимизации.
Областью техники, где широко применяют целевые функции вида (22), является проектирование оптических систем.
Минимаксные (максиминные) критерии. Пусть условия работоспособности всех выходных параметров приведены к виду (17). Такое преобразование в отношении условий (6.16) было пояснено выше, а условия (18) преобразуются в (17) путем записи следующих неравенств:

Если обозначить yk1 = —yk, то вместо условия работоспособности
типа равенства одного параметра получаем два эквивалентных ему:
условия работоспособности типа неравенства для параметров yk и
yk1. Далее введем количественную оценку степени выполнения j-го
условия работоспособности и обозначим ee sj. Цели расчета совпадают,
с целями увеличения sj (причем в первую очередь тех из sj которые
являются наименьшими).
Отсюда приходим к целевой функции вида
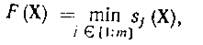 (23) (23)
|
Sj(X)=(TTj - yj)/ TTj
где m — количество условий работоспособности после их приведения к виду (17). Функцию (23) называют функцией минимума, и поскольку требуется ее максимизация, т. е.

то критерий с целевой функцией (23) называется максиминным критерием. Если бы требовалось минимизировать функцию максимума, то получился бы минимаксный критерий.
В максиминном критерии нет того главного недостатка, который
был присущ мультипликативному и аддитивному критериям. Здесь 



 влияние на целевую функцию оказывает только тот выходной параметр, который в данной точке X является наихудшим с позиций выполнения требований ТЗ. Это существенное преимущество максиминного критерия приводит в последнее время к его все более широкому распространению.
влияние на целевую функцию оказывает только тот выходной параметр, который в данной точке X является наихудшим с позиций выполнения требований ТЗ. Это существенное преимущество максиминного критерия приводит в последнее время к его все более широкому распространению.
Функция минимума не является гладкой, и условия непрерывной дифференцируемости для нее не выполняются. В связи с этим для оптимизации объектов по максиминному критерию применяют особые алгоритмы.
Рассмотрим используемые на практике представления оценок sj(X)
Иногда предлагается
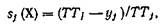 (24)
(24)
где учтено, что все условия работоспособности имеют вид (17).
Однако (24) неприемлемо, если какое-либо из ТТ j равно нулю. Более объективно цели проектирования будут отражены, если принять
 (25)
(25)
где δ j — величина, характеризующая рассеяние j -го выходного параметра; уjном — оценка его математического ожидания.
При определении δ j с помощью статистического анализа критерий превращается в статистический. Но можно δj считать постоянными величинами и задавать как исходные данные на основе априорных представлений о рассеянии выходных параметров. Тогда максиминный критерий остается детерминированным, а δj играют роль весовых коэффициентов. Указание для δj физического смысла облегчает их правильный выбор по сравнению с выбором весовых коэффициентов wj для аддитивных критериев.
Статистические критерии. Оптимизация при статистических критериях имеет целью получение максимальной вероятности Р выполнения условий работоспособности. Эту вероятность и принимают в качестве целевой функции. Тогда имеем задачу
 (26)
(26)
Применение статистических критериев позволяет добиться наименьшего процента брака при серийном производстве спроектированных изделий, т. е. получить максимальную серийнопригодность. Если при расчетах целевой функции Р(Х) учитывать статистические сведения о X, включающие данные по старению параметров, то оптимизация (26) является оптимизацией по критерию надежности. Эти обстоятельства — бесспорные преимущества статистических критериев. Главным недостатком статистических критериев является большая трудоемкость оптимизации, так как велики потери на поиск n1 в (13).
Кроме целевой функции Р(Х) при статистической оптимизации может использоваться и целевая функция (23), как об этом уже сказано выше. Вдали от границ области работоспособности ХР функция Р(Х) близка к нулю или единице и перестает быть чувствительной к изменениям X. Поэтому при максиминном критерии поиск облегчается.
Значения внешних параметров при оптимизации выбирают либо номинальными,либо исходя из принципа наихудшего случая. Большую ценность представляют результаты расчета, полученные при оптимизации в тяжелых режимах, однако выполнение такой оптимизации более сложно: во-первых, инженеру нужно определять значения внешних параметров для тяжелых режимов в исходной точке и быть уверенным в том, что эти значения остаются корректными и в процессе поиска; во-вторых, для разных выходных параметров тяжелые режимы обычно оказываются различными. Это требует решения уравнений математической модели объекта для определения каждого выходного параметра при новых значениях внешних параметров, что увеличивает затраты машинного времени.
ОБЩИЕ СВЕДЕНИЯ О МЕТОДАХ ПОИСКА
ЭКСТРЕМУМА
Выше уже отмечалось, что в подавляющем большинстве случаев задачи параметрической оптимизации при проектировании технических объектов сводятся к задачам нелинейного программирования. Поэтому именно методы нелинейного программирования является предметом дальнейшего рассмотрения.
Классификация методов. Прежде всего, отметим, что в зависимости от типа экстремумов, на поиск которых метод ориентирован, различают методы безусловной и условной, локальной и глобальной оптимизации.
Большинство методов поиска экстремума относят к методам безусловной оптимизации. Исключение составляют немногие методы, специально разработанные для поиска при наличии ограничений (например, метод проекции вектора градиента). Из сказанного не следует делать вывод о неприменимости методов безусловной оптимизации к большинству экстремальных задач 'технического проектирования, где имеют место условные экстремумы. Дело в том, что существуют и широко используются приемы сведения задач условной оптимизации к безусловной.
Подавляющее большинство методов оптимизации ориентировано на поиск локальных экстремумов. Глобальная оптимизация несравненно сложнее. К глобальным методам относят один из самых простых по своему идейному содержанию методов — метод сканирования. В этом методе вся допустимая область ХД пространства управляемых параметров разбивается на элементарные подобласти-ячейки и в центре каждой из ячеек осуществляется подсчет целевой функции. Если ячейки достаточно малы, то получается общая кар тина поведения целевой функции в ХД с выявлением всех ее экстремумов. Однако метод сканирования практически неприменим в сколько-нибудь сложных задачах из-за чрезмерно больших затрат машинного времени на решение. Здесь количество ячеек, а следовательно, и количество вариантов расчета целевой функции равно Кn, где К — количество интервалов, на которые разбивается область ХД по каждой из координатных осей, a n — размерность пространства управляемых параметров.
функции. Если ячейки достаточно малы, то получается общая кар тина поведения целевой функции в ХД с выявлением всех ее экстремумов. Однако метод сканирования практически неприменим в сколько-нибудь сложных задачах из-за чрезмерно больших затрат машинного времени на решение. Здесь количество ячеек, а следовательно, и количество вариантов расчета целевой функции равно Кn, где К — количество интервалов, на которые разбивается область ХД по каждой из координатных осей, a n — размерность пространства управляемых параметров.
На разработку методов глобальной оптимизации направлены усилия многих исследователей, однако имеющиеся к настоящему времени предложения как из-за повышенной трудоемкости, так и из-за недостаточной надежности определения глобального экстремума еще не нашли широкого распространения. Поэтому, отмечая важность решения задачи глобальной оптимизации, все же сосредоточим внимание только на методах локального поиска, как достаточно развитых и широко используемых. Дополнительным обоснованием такой позиции является следующее рассуждение. Назовем областью притяжения экстремума Э геометрическое место точек таких, что их выбор в качестве исходных для поиска градиентным методом приводит к нахождению экстремума Э при достаточно малом шаге. Если область притяжения глобального экстремума имеет объем не менее нескольких процентов от объема всей области ХД, то существует большая вероятность определения глобального экстремума с помощью локальных методов. Для этого нужно несколько раз повторить локальный поиск со случайно выбираемыми исходными точками. Как видно из рис. 4, при поисковой оптимизации движение в пространстве параметров осуществляется шагами. От величины шага зависят многие параметры поиска, например потери на поиск, точность определения экстремума, надежность поиска. Существует большое количество различных способов выбора шага, но среди них особое место занимает способ выбора оптимального по величине шага h. В этом способе при минимизации F(X) после того, как выбрано направление очередного шага, осуществляется минимизация F(X) вдоль избранного направления и перемещение в точку такого минимума. Подобная минимизация выполняется методами одномерного поиска. Поэтому, хотя при проектировании практически не встречаются объекты с единственным управляемым параметром, методы одномерного поиска представляют для САПР интерес.
Методы оптимизации объектов с несколькими управляемыми параметрами называют методами многомерного поиска или методами многопараметрической оптимизации.
Способ выбора величины шага обычно не относят к процедурам, определяющим метод поиска. Сущность метода, в первую очередь, выражается в способе выбора направления очередного шага. Если при выборе направления используется информация о первых производных целевой функции по управляемым параметрам, то метод относится к группе методов первого порядка, если ис пользуется информация о вторых производных —к группе методов второго порядка. Имеется также группа методов нулевого порядка — в них вообще производные не используются. С повышением порядка метода наблюдаются две тенденции: с одной стороны, увеличиваются потери на поиск п2, с другой стороны, уменьшаются потери на поиск n3, фигурирующие в (13). К сожалению, предсказать заранее для конкретного метода нелинейного программирования величины потерь на поиск, точность нахождения экстремума, а иногда и сам факт сходимости к экстремуму невозможно, так как характер поиска зависит не только от метода, | но и от особенностей целевых функций. Несмотря на это, знание методов поиска и характерных особенностей соответствующих им траекторий в типовых ситуациях может существенно помочь инженеру в выборе конкретных программ оптимизации для решения задач в САПР.
Рассмотрим некоторые методы поиска экстремума, являющиеся типичными представителями методов разных групп: покоординатного спуска и случайного поиска (методы нулевого порядка), градиента и наискорейшего спуска (методы первого порядка), Ньютона (метод второго порядка). Все эти методы являются методами безусловной оптимизации, их использование в задачах нелинейного программирования требует предварительного устранения ограничений.
Рассмотрение методов ведется при предположении, что управляемые параметры каким-либо образом пронормированы и потому являются безразмерными величинами, так же как и целевая функция.
Метод покоординатного спуска (метод Гаусса—Зейделя). Пусть решению подлежит задача минимизации функции F(X)
 (27)
(27)
где ХП — n -мерное пространство.
В методе покоординатного спуска направление очередного шага выбирается вдоль какой-либо одной координатной оси, например оси параметра х1. Движение в этом направлении производится в сторону, в которой наблюдается уменьшение F(X), и выполняется до тех пор, пока F(X) уменьшается. Далее движение начинается вдоль новой координатной оси, например параметра х2, и т. д. После цикла спусков вдоль всех п осей производится новый цикл, если экстремум еще не найден. Когда ни по одной из осей невозможно перемещение с уменьшением функции F(X) с шагом h> hmin, поиск прекращается, и полученная точка X признается за принадлежащую малой окрестности экстремальной точки X* (здесь hmin —задаваемое ограничение шага снизу).
Пример траектории покоординатного спуска в двумерной задаче показан на рис. 5, где линии равного уровня целевой функции F(X) соответствуют ее значениям, равным а1 — а4, причем a1 < a2 < C < а3 < a4. Из исходной точки Х0 движение начато вдоль оси х2. Пусть используется вариант метода с одномерной минимизацией F(X) на выбранных направлениях. Тогда после определения оптимального шага произойдет перемещение в точку X1. Далее выполняется смена направлений движения. На новом направлении вдоль оси х1 шаг будет совершен в точку Х2 и т. д.
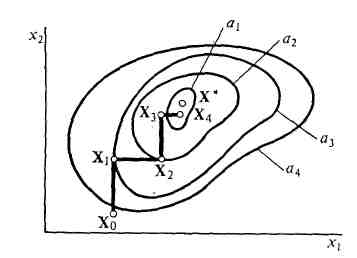
Рисунок 5. Иллюстрация поиска экстремума методом покоординатного спуска
Методы случайного поиска. Методы случайного поиска отличает от других рассматриваемых здесь методов та черта, что траектория случайного поиска не предопределена заданием всех необходимых исходных данных —вида целевой функции F(X), координат исходной точки, величины шага. Повторяя поиск при одинаковых исходных данных, будем получать разные траектории.
Существует много разновидностей методов случайного поиска. В простейшем из них направление поиска выбирается случайно, проверяется его перспективность и при благоприятном результате проверки осуществляется шаг в этом направлении. При отрицательном результате проверки случайным образом выбирается новое направление и далее процесс повторяется.
Случайный выбор направления движения из точки Xk выполняется с помощью уже рассмотренных выше алгоритмов выработки случайных чисел. Если выработать n- значений равномерно распределенной в интервале [—1, +1] случайной величины, то можно рассматривать эти значения как элементы n-мерного случайного вектора, задающего направление в n-мерном пространстве. Проверка перспективности направления выполняется путем расчета и сопоставления значений целевой функции F(X) в двух точках, одной из них является точка Xk, другой — точка Xk+1, находящаяся на выбранном направлении и отстоящая от Xk на величину шага. Если F(X)< Xk+1, то новой отображающей точкой будет Xk+1, иначе попытка неудачна и остается отображающая точка Xk. Поиск обычно прекращают, если было выполнено подряд L неудачных попыток продвижения, где L относится к исходным данным.
Метод градиента. Известно, что вектор-градиента в каждой точке совпадает с направлением наибыстрейшего возрастания целевой функции, т. е. локально наилучшим является градиентное направление при максимизации или антиградиентное направление при минимизации. Это свойство градиента и используется в методе градиента. В соответствии с методом в каждой отображающей точке Xk рассчитывается градиент целевой функции:


Рисунок 6. Иллюстрация поиска экстремума методом градиента (а) и методом наискорейшего спуска (б).

|
и при решении задачи (6.27) шаг осуществляется в антиградиентном направлении в новую отображающую точку, имеющую координаты
где h —величина шага поиска.
Если F( Xk+1 )< F( Xk ), то вычисляется градиент grad F (Xk+1) уже в точке Xk+l и делается новый шаг той же величины h. Если F (Xk+1) > F( Xk ), то такая ситуация отождествляется с заметной кривизной линий равного уровня у функции F(X), что требует продолжения поиска с уменьшенным шагом. Если шаг уменьшен до некоторого заданного предела h min, но по-прежнему F( Xk+1 ) ≥ F( Xk ), то считается, что точка Xk находится в h min -окрестности экстремальной точки и принимается X*≈ Хk.
На рис. 6 а) показана траектория поиска минимума некоторой функции, представленной своими линиями равного уровня и точкой минимума X*, с помощью градиентного метода. При использовании геометрических представлений полезно помнить, что градиентное направление является, нормальным к линиям (в общем случае к гиперповерхностям) равного уровня. Именно это свойство градиента и определило вид траектории рис. 6 а).
Метод наискорейшего спуска. Этот метод можно считать разновидностью градиентного метода в условиях, когда величина шага h рассчитывается оптимальной с помощью одномерной минимизации целевой функции вдоль градиентного направления. Иногда из алгоритмов наискорейшего спуска исключают процедуру одномерной минимизации и стратегия изменения величины шага h принимается такой же, как в основном градиентном методе. Тогда различие между методами градиента и наискорейшего спуска будет заключаться в том, что по-разному определяются направления движения. Если для очередной точки Хk+1 выполняется условие F( Xk+1 )<F( Xk ), т. е. имеет место улучшение целевой функции, то наискорейший спуск требует продолжения движения в прежнем направлении без расчета grad F( Xk+1 ). Действия, предписываемые методами градиента и наискорейшего спуска, будут одинаковыми только в тех точках, в которых
F( Xk+1 )≥ F( Xk )

 Траектория поиска минимума той же целевой функции F(X), что и на рис. 6 а), методом наискорейшего спуска показана на рис. 6 б).
Траектория поиска минимума той же целевой функции F(X), что и на рис. 6 а), методом наискорейшего спуска показана на рис. 6 б).
Из сопоставления рис. 6 а) и 6 б) видно, что метод наискорейшего спуска приводит к выполнению большего количества шагов, чем метод градиента, но в среднем один шаг при методе наискорейшего спуска требует меньшего объема вычислений — анализ чувствительности для определения градиента выполняется реже.
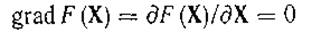 (28) (28)
|
Метод Ньютона. Метод Ньютона при оптимизации совпадает с одноименным методом решения систем алгебраических и трансцендентных уравнений. Это объясняется тем, что задача оптимизации при использовании необходимых условий экстремума
сводится к решению системы уравнений (28). Формула метода Ньютона, применительно к (28) имеет вид
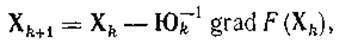
|
где Юk —матрица Гессе целевой функции F (Х), вычисленная в точке Xk.
Скорость сходимости к экстремуму в методе Ньютона выше, чем в методах нулевого или первого порядка. Однако, как уже отмечалось ранее, не во всех задачах имеется сам факт сходимости. Главный недостаток метода Ньютона для задач оптимизации проектируемых устройств заключается в отсутствии простых и экономичных алгоритмов вычисления матрицы Гессе.
Одномерный поиск. Определение оптимального шага означает поиск минимума функции F (X) вдоль избранного направления g, т. е.

где Хk —текущая отображающая точка.
Например, в методе наискорейшего спуска g есть антиградиентное направление.
Из методов одномерной оптимизации наиболее часто используют метод полиномиальной аппроксимации и метод Фибоначчи.
В методе полиномиальной аппроксимации сначала отыскивается интервал изменения h, на котором должна находиться оптимальная точка h*. Простейший способ определения такого интервала заключается в последовательном вычислении значений
 (29)
(29)
до тех пор, пока очередное значение функции не станет больше предыдущего. Зная интервал, по его двум граничным и одной внутренней точкам можно построить интерполяционный полином
f (h) = а0 + a1h + a2h2 (30)
и задача отыскания h* преобразуется в задачу минимизации полинома (30).
В результате получается оценка/г*, равная h* = — ах/(2а2). Если
окажется, что f(h*) превышает какое-либо из трех вычисленных на интервале значений функции, то оценка h * неудовлетворительна и следует уменьшить интервал, на котором ищется минимум. Обычно одна из
трех точек отождествляется с исходной точкой (при h= 0), поэтому
минимальное количество вычислений целевой функции при одномерном поиске равно трем. Однако это будет только при удачном выборе
значения h1 в последовательности (29) и при получении оценки h *
без необходимости ее уточнения. Следовательно, одномерный поиск,
как правило, требует более чем трехкратного вычисления целевой
функции.
Сведение задач условной оптимизации к безусловной. Основным методом перехода от условной оптимизации к безусловной является метод штрафных функций. Пусть имеем задачу
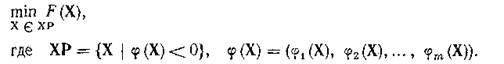
Идея метода штрафных функций заключается в замене исходной
целевой функции F(X) на функцию Ф (Х), которая должна быть максимально близкой к функции F( X ) в области работоспособности ХР
(при выполнении всех ограничений) и быть существенно больше, чем
функция F( X ), вне области ХР. Другими словами, нарушение ограничений можно рассматривать как наложение штрафа в виде ухудшения новой целевой функции Ф (Х).
Обычно функция Ф (Х) образуется суммированием исходной целевой функции F( X ) и функции штрафа θk(X):
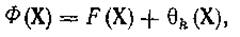
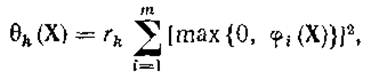
|
где в качестве θk(X) часто выбирается следующая функция:
где rk> 0.
Величина штрафа θk(X) зависит от коэффициента rk: чем больше rk, тем больше штраф, тем ближе должны находиться условный минимум F( X ) и безусловный минимум Ф (Х); при rk ™¥ эти минимумы становятся неразличимыми. Здесь следует отметить, что если условный минимум функции F(X) лежит внутри области ХР, то он одновременно является и безусловным, так как для X Î ХР всегда max {0, ji(Х)} = 0. Тогда минимум функции F(X) мог быть найден и без введения штрафа. Если же условный минимум функции F(X) лежит на границе области ХР, то минимумы функций F( X ) и Ф (Х), как правило, не совпадают и для их сближения нужно увеличивать rk. Однако чем больше rk, тем ближе должна быть выбрана исходная точка поиска к экстремальной точке, иначе могут возникнуть неприятности типа переполнения разрядной сетки ЭВМ.
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1727; Нарушение авторских прав?; Мы поможем в написании вашей работы!