Необходимые и достаточные условия экстремума

Классические методы безусловной оптимизации применяют в тех случаях, когда известен вид целевой функции F( X ), т. е. дано ее аналитическое вы­ражение, и предполагается, что F( X ) не менее чем дважды дифферен­цируема по управляемым параметрам. Тогда для определения экстре­мума используют необходимые и достаточные условия безусловного экстремума. Эти условия легко получить с помощью разложения F( X ) в окрестностях экстремальной точки в ряд Тейлора для функции y_j{X).

Имеем

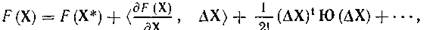(7)

где

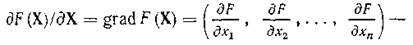
градиент целевой функции; ΔХ = X — X*; Ю — матрица Гессе (ее элементы — вторые производные целевой функции по управляе­мым параметрам).

Очевидно, что условие (2) может выполняться, только если линей­ный член<grad F( X ), ΔХ > равен нулю. Следовательно, необходимым условием экстремума является условие

grad F (X) = 0.

Все точки, в которых выполняется это условие, называют ста­ционарными. Но неравенство (2) не обязательно выполняет­ся в стационарной точке. Для его выполнения нужно, чтобы квад­ратичный член в (7) при любых ΔХ оставался отрицательным, т. е.

(ΔХ)^tЮ(ΔХ)<0. (8)

Условие (8) есть достаточное условие максимума. Матрицу Ю, удовлетворяющую условию (8) при любых ΔХ, называют отрица­тельно - определенной матрицей, а в случае (АХ)'Ю(АХ)> 0 для любых ΔХ — положительно - определенной матрицей. Поэтому достаточные условия экст­ремума можно представить как требование отрицательной опреде­ленности матрицы Гессе для максимума или положительной опре­деленности для минимума в экстремальной точке.

Итак, если известно выражение F(X), то достаточно продифферен­цировать целевую функцию по управляемым параметрам и приравнять производные нулю. Решение полученной таким образом системы урав­нений даст стационарную точку. Далее нужно убедиться в том, что это действительно экстремальная точка, с помощью проверки вы­полнения достаточных условий. Если достаточные условия не выпол­няются, то имеем не экстремальную, а седловую точку.

К сожалению, отсутствуют легко проверяемые признаки много­экстремальных ситуаций. Зная координаты какой-либо экстремальной точки, нельзя сделать никаких заключений о локальном или гло­бальном характере этого экстремума, не исследуя F( X ) во всей обла­сти определения. Исключением являются задачи, где целевая функ­ция — выпуклая при минимизации или вогнутая при максимизации. Выпуклость (или вогнутость) есть достаточный признак одноэкстремальности. Но в задачах проектирования при отсутствии аналитичес­кого задания целевых функций проверка F( X ) на выпуклость или вог­нутость, как правило, невозможна.

При известных аналитических выражениях целевой функции и ог­раничений условная оптимизация осуществляется с помощью мето­да неопределенных множителей Лагранжа, который непосредственно применим к задачам с ограничениями типа равенств (5). В соответствии с этим методом задача условной макси­мизации F( X ) заменяется задачей безусловной максимизации функ­ции Лагранжа

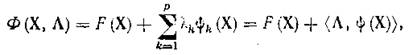
где Λ = (λ₁, λ₂,..., λ_p) — вектор неопределенных множителей Лагранжа;

ψ _k(X) — k -е ограничение из группы ограничений-равенств; р — количество ограничений.

Значения функций Ф(Х, Λ) и F (X) при XÎХР совпадают, так как в области работоспособности ψ _k(X) = 0. Тогда, если найдем mах Ф(Х, Λ) при XÎХР, то он будет одновременно, и условным максимумом функции F( X ). Поэтому находим максимум Ф(Х, Λ), используя не­обходимые условия экстремума

(9)

(10)

и решая полученные уравнения (9) и (10). Из (10) видно, что ста­ционарная точка функции Ф(Х, Λ) будет принадлежать области ХР, а следовательно, она дает решение и исходной задачи условное! мак­симизации функции F(X).

Поисковая оптимизация. Об­ласть математики, исследующая вопросы теории и методы решения задач условной оптимизации, по­лучила название математического программиро­вания. Известны такие разделы математического программирова­ния, как линейное, выпуклое, ге­ометрическое и др., занимающи­еся исследованием частных случаев задач математического программи­рования. В процессе проектиро­вания технических объектов наиболее часто встречаются задачи математического программирования со следующей формулировкой: найти максимум (или минимум) целе­вой функции F( X ) в области ХР, определяемой (6), где целевая функция и функции-ограничения являются нелинейными функциями управляемых параметров. Такую задачу обычно записывают в виде

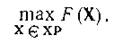(11)

Рисунок. Линии равного уровня функции с двумя максимумами.

Задача (11) есть задача нелинейного программирования. В отдельных случаях при проектировании удается задачу поставить так, что F( X ) и ограничения будут линейными функ­циями своих аргументов. Тогда имеет место задача линей­ного программирования.

Классические методы нахождения экстремумов целевых функций непосредственно в САПР практически не применяются, так как слу­чаи аналитического задания функций в задаче (11) крайне редки. Ха­рактерной ситуацией является наличие алгоритмических математи­ческих моделей. В связи с этим определение значений целевых функ­ций, функций-ограничений и их градиентов возможно только через численное решение систем уравнений, подсчет функционалов и вы­полнение других необходимых алгоритмов. В такой ситуации исполь­зуют поисковую оптимизацию, при которой поиск цели — экстремальной точки в пространств управляемых парамет­ров— осуществляется последовательными шагами, ведущими от ис­ходной точки Х₀ через некоторые промежуточные отображающие точки Х_к в заданную ε-окрестность точки экстремума X*.

При рассмотрении методов поисковой оптимизации полезны не­которые геометрические представления. Будем называть последо­вательность отображающих точек X_k, соединенных отрезками пря­мых, траекторией поиска. Геометрическое представление функций дается в виде поверхностей отклика (при раз­мерности пространства более двух имеем гиперповерхности отклика). В свою очередь, поверхности отклика на рисунках представляются в виде совокупности линий равного уровня. Линия равного уровня (при п> 2 — поверхность или гиперповерхность равного
уровня) имеет уравнение F(X) = а и является геометрическим место
точек в пространстве управляемых параметров, в которых значения
целевой функции равны a.

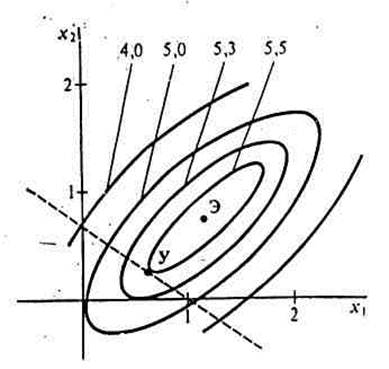
Рисунок 2. Линии равного уровня одноэкстремальной функции

Рис. 6.3. Линии равного уровня функции с седловой точкой

Воспользуемся геометрическими представлениями для графической иллюстрации некоторых из введенных здесь понятий. Во всех
случаях будем использовать двумерное пространство управляемы;
параметров X = (x₁, х₂). На рис. 1 показаны линии равного уровня
некоторой функции F(X) с двумя максимумами в точках А и Б (значения функции указаны на рисунке рядом с линиями равного уровня).
Здесь точка А — точка глобального максимума, так как F( A ) превы­шает значение F (Б).

На рис. 2 приведен пример одноэкстремальной функции

F(X) = — 1,1*x₁² — 1,5x₂²+2x₁*x₂ + x₁+5, (12)

ее линии равного уровня на рисунке сплошные, точка Э — точка безусловного экстремума, Э = (1,15, 0,77).

Пусть имеется ограничение x₁ + 1,5 x₂ — 1 = 0, соответствующая ему линия показана на рис. 2 пунктиром. Очевидно, что точка условного экстремума Y здесь не совпадает с точкой безусловного экстремума Э.

На рис. 3 показаны линии равного уровня функции

F (X) = — 0,5*x₁² — 0,25x₂² - x₁*x₂ - 3x₁

Для этой функции в стационарной точке С = (1,— 2) выполняются необходимые, но не выполняются достаточные условия экстремума. Следовательно, С — седловая точка.

На рис..1 седловой точкой будет тонка В.

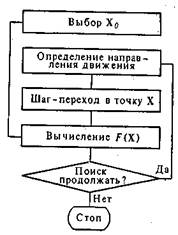
'Этапы вычислительного процесса при оптимизации. Перед началом поиска, выбирается некоторая исходная точка Х₀ в пределах допустимой области ХД. Далее вычислительный процесс состоит из по­следовательности шагов. На каждом шаге сначала выбирается направление движения. Затем произво­дится сам шаг в пространстве управ­ляемых параметров, в результате из предыдущей точки Х_k осуществляется переход в новую точку Х_k+1. В этой точке вычисляется значение целевой функции F(X_k+1), благодаря чему мож­но судить о достигнутом успехе. Шаг заканчивается проверкой условий пре­кращения поиска: если условия вы­полнены, то поиск заканчивается, ина­че делается переход к новому шагу. Изложенная схема вычислений иллю­стрируется рис. 4.

Рис. 4. Схема вычислений при поисковой оптимизации.

Выше неоднократно отмечалось, что при алгоритмических математических моделях цена каждого варианта анали­за достаточно высока. В процессе же оптимизации приходится выполнять анализ многократно.

Обозначим через п ₁ и п₂ количества вариантов анализа работы объекта на этапе вычисления целевой функции и на этапе определения направления поиска соответственно, а через n ₃ — количество шагов 'поиска. Пусть Т_м1 — затраты машинного времени на один вариант анализа работы объекта. Тогда общее время решения задачи опти­мизации на ЭВМ

T_K = T_M1(n₁ + n₂)n₃. (13)

Значения n ₁, п₂ и п₃ характеризуют эффективность принятой стра­тегии поиска с позиций затрат машинного времени, эти параметры обычно называют потерями на поиск и относят к основным критериям эффективности алгоритмов. Кроме потерь на поиск к пока­зателям эффективности относят точность определения экстремальной точки, надежность поиска, понимаемую как вероятность получения -решения задачи с заданной точностью. F

Дата добавления: 2014-01-07