Условия существования минимума

Запишем разложение функции f(x) в ряд Тейлора в окрестно­сти точки х* с точностью до малых 3-го порядка. Заметим, что х и dx везде будут выступать в качестве векторов, за исключением некоторых случаев, о которых будет сказано особо. Индекс Т обозначает транспонирование.

F(x)=f(x*)+G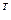(x*)∆x+(1/2)∆x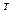H(x*)∆x+O(∆x) (1)

где G(х*) - вектор-градиент в точке х(0);

Н(x*) - матрица вторых производных (матрица Гессе).

Напомним, что условие стационарности точки х* есть равен­ство нулю градиента: G(х*) = 0.

В точке минимума приращение функции ∆f(x)=f(x)-f(x*) должно быть больше нуля при любом x, удовлетворяющем условию х-х* <ε.

Это условие записывают также следующим образом: х принадлежит sph(x*,ε), то есть точка х принадлежит множеству точек сферы радиусом ε с центром в точке x*. Тогда из (1.1) следует положительность квадратичной формы:

∆x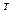H(x*)∆x>0

Последнее выражение означает положительную определенность матрицы Н в точке х*.

Заметим, что при построении алгоритмов поиска минимума должно быть введено условие останова. Это условие для гладких функций обычно состоит в проверке близости модуля градиента к нулю. С другой стороны, алгоритмы поиска должны быть рассчита­ны на то, что в точке минимума градиент может не существовать. Тогда в общем случае правило останова должно быть реализовано в виде непосредственной проверки условия ∆f(x)>0.

Дата добавления: 2014-01-07