
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Минимизация по правильному симплексу
|
|
|
|
Определение:
Правильным симплексом в пространстве Еn называется множество из n+1 равноудаленных друг от друга точек (вершин симплекса).
Отрезок соединяющих две вершины, называются ребром симплекса.
Например: в пространстве Е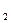 правильным симплексом является совокупность вершин равностороннего треугольника.
правильным симплексом является совокупность вершин равностороннего треугольника.
Если Х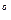 - одна из вершин правильного симплекса в Еn, то координаты остальных n вершин X
- одна из вершин правильного симплекса в Еn, то координаты остальных n вершин X ,…,X
,…,X можно найти по формулам:
можно найти по формулам:
Х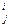 =
=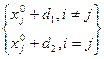 (2)
(2)
где d =a(
=a( -1)/n
-1)/n , d
, d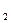 =a(
=a( +n-1)/n
+n-1)/n , а-длина ребра
, а-длина ребра
Определение:
Вершину Х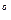 симплекса, построенного по формулам (1), будем называть базовой.
симплекса, построенного по формулам (1), будем называть базовой.
В алгоритме симплексного метода используется следующее важное свойство правильного симплекса: по известному симплексу можно построить новый симплекс путем отражения какой-либо вершины, например X симметрично относительно центра отражения X
симметрично относительно центра отражения X остальных вершин симплекса. Новая и старая вершины X
остальных вершин симплекса. Новая и старая вершины X ^ и X
^ и X связаны соотношением:
связаны соотношением:
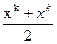 =x
=x , где x
, где x =
=
В результате получается новый правильный симплекс с тем же ребром и вершинами
X ^=2 x
^=2 x -x
-x , x
, x , i=0,…,n, i≠k
, i=0,…,n, i≠k
Таким образом происходит перемещение симплекса в пространстве Еn.
Изобразим на рисунке пример построения нового симплекса в Е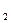 отражением точки X
отражением точки X :
:
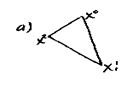
а) начальный симплекс Х , Х
, Х , Х
, Х ;
;
|
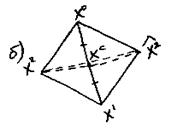
б) новый симплекс Х , Х
, Х , X
, X ^;
^;
центр отражения – точка Х =(Х
=(Х +Х
+Х )/2
)/2
|
Поиск точки min-ма функции f(x) с помощью правильных симплексов производится следующим образом.
На каждой итерации сравниваются значения f(x) в вершинах симплекса. Затем производится процедура отражения той вершины, в которой f(x) принимает max-ое значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще одну попытку отражения для вершины со следующим по величине значением f(x). Если и она не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину Х старого симплекса, в которой функция принимает min-ое значение. Поиск точки min-ма f(x) заканчивают, когда, либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становится достаточно малыми.
старого симплекса, в которой функция принимает min-ое значение. Поиск точки min-ма f(x) заканчивают, когда, либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становится достаточно малыми.
Один из вариантов алгоритма этого метода:
ШАГ 0:
Выбрать параметр точности 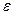 , базовую точку Х
, базовую точку Х , ребро а и построить начальный симплекс по формулам (1). Вычислить f(Х
, ребро а и построить начальный симплекс по формулам (1). Вычислить f(Х ).
).
ШАГ1:
Вычислить значение f(x) в вершинах симплекса X ,…,X
,…,X .
.
ШАГ2:
Упорядочить вершины симплекса X ,…,X
,…,X так, чтобы f(Х
так, чтобы f(Х )
)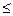 f(X
f(X )
)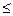 …
…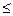 f(X
f(X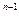 )
)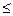 f(X
f(X )
)
ШАГ3:
Проверить условие
 (2)
(2)
Если оно выполняется, то вычисления прекратить, полагая Х*≈Х , f*≈f(Х
, f*≈f(Х ). В противном случае перейти к шагу 4.
). В противном случае перейти к шагу 4.
ШАГ4:
Найти x =
= и выполнить отражение вершины х
и выполнить отражение вершины х :
:
х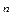 ^=2 x
^=2 x -х
-х . Если f(х
. Если f(х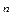 ^)<f(х
^)<f(х ), то положить х
), то положить х = х
= х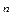 ^ и перейти к шагу2. Иначе перейти к шагу5.
^ и перейти к шагу2. Иначе перейти к шагу5.
ШАГ5:
Найти x =
=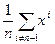 и выполнить отражение вершины х
и выполнить отражение вершины х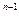
х ^=2 x
^=2 x -х
-х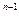 . Если f(х
. Если f(х ^)<f(х
^)<f(х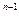 ), то положить х
), то положить х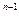 = х
= х ^ и перейти к шагу 2. Иначе перейти к шагу 6.
^ и перейти к шагу 2. Иначе перейти к шагу 6.
ШАГ6:
Перейти к новому правильному симплексу с вдвое меньшим ребром,считая базовой вершиной х . Остальные n-вершин симплекса найти по формуле х
. Остальные n-вершин симплекса найти по формуле х =(х
=(х +х
+х )/2, i=1,…,n
)/2, i=1,…,n
Перейти к шагу 1.
Замечания:
1. Следует иметь в виду, что если функция f(x) многомодальна, то описательным методом может быть найдена точка локального, а не глобального min-ма f(x).
2. Если ограниченность снизу целевой функции не очевидна, то в алгоритм метода следует включить дополнительную процедуру останова.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1323; Нарушение авторских прав?; Мы поможем в написании вашей работы!