
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поиск точки min-ма по деформируемому симплексу
|
|
|
|
Алгоритм, описанный для минимизации по правильному симплексу, можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения.
А именно, положение новой вершины х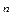 ^ вместо вершины х
^ вместо вершины х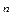 , соответствующей наибольшему значению функции, находится сравнением и выбором наименьшего среди значений целевой функции в точках:
, соответствующей наибольшему значению функции, находится сравнением и выбором наименьшего среди значений целевой функции в точках:
z = x
= x -
- (x
(x -x
-x ), 0<
), 0< <1;
<1;
z = x
= x +
+ (x
(x -x
-x ), 0<
), 0< <1; (1)
<1; (1)
z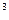 = x
= x +
+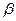 (x
(x -x
-x ),
), 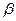 ≈1;
≈1;
z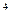 = x
= x +
+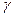 (x
(x -x
-x ),
),  >1.
>1.
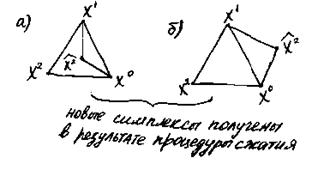
Геометрическая иллюстрация этих процедур для пространства Е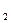 ;
;
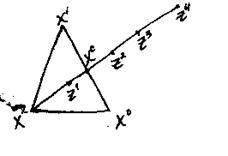
z , z
, z , z
, z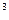 , z
, z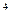 - пробные точки, для перехода к новому симплексу.
- пробные точки, для перехода к новому симплексу.
Так как величина  Є(0;1), то выбор точек z
Є(0;1), то выбор точек z и z
и z соответствует сжатию симплекса;
соответствует сжатию симплекса; 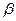 ≈1, поэтому выбор точки z
≈1, поэтому выбор точки z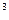 соответствует отражению, а
соответствует отражению, а 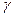 >1 и выбор точки z
>1 и выбор точки z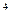 приводит к растяжению симплекса.
приводит к растяжению симплекса.
Например:

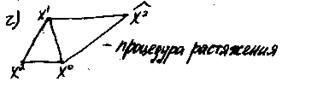
Численные эксперименты показывают, что этот алгоритм хорошо работает в пространстве Еn для n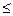 6.
6.
Отметим, что при деформациях утрачивается свойство правильного исходного симплекса. Поэтому не стремясь к правильности начального симплекса, его строят из произвольной базовой точки х ЄЕn по формулам:
ЄЕn по формулам:
х =х
=х +
+ е
е (2)
(2)
где е -iй базисный вектор;
-iй базисный вектор;  -параметр симплекса.
-параметр симплекса.
На практике часто применяется следующий набор параметров  ,
,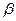 и
и  для выбора пробных точек z
для выбора пробных точек z в формулах (1):
в формулах (1):
 =1/2;
=1/2; 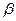 =1 и
=1 и  =2
=2
Опишем алгоритм поиска точки min-ма функции по деформирующему симплексу:
ШАГ 0:
Выбрать параметр точности 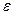 , параметры
, параметры  ,
,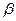 и
и  , базовую точку х
, базовую точку х , параметр а и построить симплекс по формулам (1) или (2). Вычислить f(х
, параметр а и построить симплекс по формулам (1) или (2). Вычислить f(х ).
).
ШАГ1:
Вычислить значение функции в вершинах симплекса х ,…,х
,…,х .
.
ШАГ2:
Упорядочить вершины х ,…,х
,…,х так, чтобы f(х
так, чтобы f(х )
)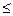 …
…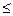 f(х
f(х )/
)/
ШАГ3:
Проверить достижение заданной точности (условие:  ). Если оно выполняется, то вычисления завершить, полагая х*≈х
). Если оно выполняется, то вычисления завершить, полагая х*≈х , f*≈f(Х
, f*≈f(Х ). Иначе перейти к шагу4.
). Иначе перейти к шагу4.
ШАГ4:
Найти x =
= и пробные точки z
и пробные точки z , k=1,…,4 по формулам (1).
, k=1,…,4 по формулам (1).
Найти f(z )=min f(z
)=min f(z ). Если f(z
). Если f(z )<f(х
)<f(х ), то положить х
), то положить х =z
=z и перейти к шагу2. Иначе перейти к шагу5.
и перейти к шагу2. Иначе перейти к шагу5.
ШАГ5:
Уменьшить симплекс, полагая х =(х
=(х +х
+х )/2, i=1,…,n и перейти к шагу 1.
)/2, i=1,…,n и перейти к шагу 1.
Замечание:
Для того, чтобы избежать сильной деформации симплекса, алгоритм иногда дополняют процедурой обновления.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 329; Нарушение авторских прав?; Мы поможем в написании вашей работы!