Широкополосные и узкополосные процессы

Если энергетический спектр случайного процесса с непре­рывным спектром сосредоточен в относительно узкой полосе

частот Dw около некоторой фиксированной частоты w ₀ (рис. 1.2 а), причём Dw ‹‹ w ₀ то такой процесс называется узкопо­лосным. Если же указанное условие не выполняется, то есть спектральная плотность средней мощности сохраняет постоянное значение до очень высоких частот (рис. 1.2 б), то случайный процесс называется широкополосным. Для узкополосных и ши­рокополосных процессов корреляционные функции будут значи­тельно отличаться по длительности.

Для широкополосного процесса согласно (1.10)корреляционная функция будет отличаться от нуля в узкой области значений t около начала координат

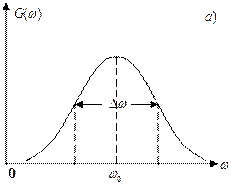Рис. 1.2

Полезной математической идеализацией широкополосного процесса является процесс, спектральная плотность которого

равномерна во всей области частот. Такой процесс по анало­гии с белым светом называется белым шумом. Корреляцион­ная функция белого шума равна

(1.12)

т.е. представляет собой дельта-функцию в начале координат. Коэффициент корреляции для белого шума равен

(1.13)

Следовательно, для белого шума значения процесса в любые сколь угодно близкие моменты времени не коррелированы. Поэ­тому белый шум иногда называют абсолютно случайным про­цессом.

Белый шум является математической идеализацией. В реальных процессах достаточно близкие значения практически зависимы. Кроме того, реальные процессы имеют конечную мощность, а для белого шума мощность процесса бесконечна. Однако на практике часто приходится рассматривать прохожде­ние широкополосного процесса через различные радиотехниче­ские устройства, полоса пропускания которых ограничена и много уже ширины энергетического спектра входного процесса. В этом случае замена реального процесса идеальным белым шумом не вносит существенных погрешностей, значительно уп­рощая при этом математические выкладки.

Отметим еще, что понятие 'белый шум" относится толь­ко к спектральной картине случайного процесса и не затрагивает вопроса О законах распределения. Как уже отмечалось выше, случайные процессы могут иметь одинаковые корреля­ционные функции и, следовательно, энергетические спектры,но различные законы распределения. Так и белые шумы с одина­ковыми энергетическими спектрами могут иметь различные законы распределения.

Определим теперь корреляционную функцию узкополосного случайного процесса со спектральной плотностью (рис. 1.3). (1.14)

Вводя вместо 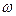новую переменную интегрирования , равную величине расстройки, вместо (1.1.11), получим

(1.15)

Рис. 1.3

Так как для узкополосных процессов ширина спектра ма­ла по сравнению с 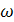, а функция расположена в об­ласти низких частот, то верхние пределы интегрирования мож­но распространить до бесконечности (здесь рассматриваетсятолько положительная ветвь исходного процесса). Вводя обозначения

(1.16)

для корреляционной функции узкополосного процесса оконча -тельно находим

(1.17)

Так как энергетический спектр сосредоточен вузкой полосе частот около 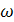₀, а спектр расположен в низкочастотной области, то функции и будут медленно меняющимися функциями по сравнению c и

Если дополнительно предположить, что энергетический спектр узкополосного процесса симметричен относительно цент­ральной частоты , то энергетический спектр 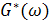будет симметричен относительно начала координат. В этом случае функция , так как для неё подынтегральное выраже­ние в (1.15) является нечётной функцией, и

. (1.18)

Следовательно, корреляционная функция узкополосного случай­ного процесса с симметричным относительно средней частоты энергетическим спектром равна умноженной на корреляционной функции которая соответствует низкос частотному процессу со спектром 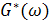, полученному из ис­ходного процесса смещением спектра на величину в об­ласть низких частот. Сказанное иллюстрируется рис. 1.3 б. Интервал корреляции узкополосного процесса согласно (1.11) будет равен

В качестве примера определим корреляционную функцию реализации процесса в виде отрезка гармонического колебания длительностью Т

(рис. 1.4 а):

(1.19)

Амплитудно-фазовый спектр такого сигнала определяется вы­ражением. Его энергетический спектр согласно опре­делению (1.1.2) будет равен:

(1.20)

Корреляционная функция отрезка гармонического колебания будет равна

(1.21)

Определение кор­реляционной функции сог­ласно (1.21) требует использования теории вы­четов и вызывает затруд­нения. Поэтому в рас­сматриваемом случае для вычисления корреля­ционной функции восполь­зуемся выражением

(1.22)

Рис. 1.4

В данном случае имеем

(1.23)

После тригонометрических преобразований и интегрирования по­лучим

График полученной корреляционной функции показан на рис. 1.4б. Замечаем, что первый- из сомножителей представляет собой корреляционную функцию одиночного прямоугольного импульса, т.е. огибающей радиоимпульса, спектр которой по форме совпадает со спектром радиоимпульса, но сдвинут в об­ласть низких частот.

Дата добавления: 2014-01-07