Примеры алгоритмов

Рассмотрим несколько классических алгоритмов, преобразующих как числовую, так и логическую информацию. Применительно к некоторым примерам продемонстрируем проявление основных свойств алгоритмов.

Пример 1. Алгоритм Евклида нахождения наибольшего общего делителя Z двух натуральных чисел a и b.

Идея алгоритма выражается следующим свойством (при a > b)

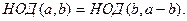
1. Если a = b, то присвоить z значение a, Конец.

2. Если a > b, то перейти к пункту 4, иначе - к пункту 3.

3. Присвоить b значение b - a, перейти к пункту 1.

4. Присвоить a значение a - b, перейти к пункту 1.

Алгоритм Евклида обладает всеми вышеперечисленными основными свойствами. На каждом шаге четко определена операция и какой шаг выполняется следующим (однозначность). Можно доказать, что алгоритм дает правильный результат для любых двух значений a и b из натурального ряда (результативность и массовость). С другой стороны, легко убедиться, что алгоритм работает бесконечно при неположительных значениях a или b. Исходные данные – числа, т.е. дискретная информация. Наконец, все операции алгоритма легко выполнимы.

Пример 2. Решето Эратосфена – алгоритм поиска всех простых чисел, не превосходящих заданного числа N.

1. Выписать последовательно все целые числа от 2 до N. Перейти к пункту 2.

2. Положить P = 2. Перейти к пункту 3.

3. Если , то перейти к пункту 4, иначе к пункту 6.

4. Начиная с числа (включительно), зачеркнуть в последовательности чисел каждое P – e число (независимо от того, было ли оно уже зачеркнуто). Перейти к пункту 5.

5. Первое после P не зачеркнутое число последовательности считать новым значением P. Перейти к пункту 3.

6. Конец. Все незачёркнутые числа последовательности являются простыми.

Самостоятельно убедитесь в том, что для этого алгоритма выполняются все вышеперечисленные основные свойства. Попробуйте доказать, что Решето Эратосфена действительно находит все натуральные простые числа от 2 до N.

Пример 3. Алгоритм разложения натурального числа N на простые множители. При составлении этого алгоритма мы воспользуемся двумя предыдущими, считая их уже известными операциями.

1. Составить в порядке возрастания последовательность простых чисел от 2 до N. Положить P=2, перейти к пункту 2

2. Если N – простое число (находится в выписанной последовательности), то перейти к пункту 7, иначе к пункту 3.

3. Если , то перейти к пункту 4, иначе к пункту 6.

4. Найти следующее за P простое число. Положить P равным этому числу. Перейти к пункту 5.

5. Если , то перейти к пункту 7, иначе - к пункту 3.

6. Положить N равным N/P. Выписать P как очередной простой множитель. Перейти к пункту 3.

7. Выписать N как последний простой множитель. Конец.

Алгоритмы сортировки

Задача сортировки формулируется следующим образом. Имеется массив из N чисел 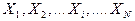,. Необходимо расположить его элементы в порядке неубывания. Разберем несколько алгоритмов сортировки.

Пример 4. Метод «взбалтывания» (метод «пузырька») основан на сравнении соседних элементов массива.

1. Положить i=1.

2. Сравнить элементы массива 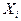и 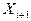. Если 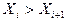, то поменять их местами. Перейти к пункту 3.

3. Увеличить i на 1. Если , то перейти к пункту 2, иначе - к пункту 4.

4. Уменьшить N на 1. Если , то перейти к пункту 1, иначе к пункту 5.

5. Конец. Получен упорядоченный массив.

Пример 5. Метод сортировки вставками. Сущность метода заключается в том, что в уже упорядоченный массив вставляется новый элемент.

1. Положить S=2.

2. В массиве находим место, куда нужно вставить элемент 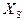. Для этого сравниваем элементы этого массива, с 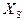начиная с 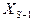до . Находим первый элемент массива, меньший 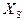. Тогда 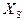надо поставить сразу вслед за этим элементом.

3. Увеличиваем S на 1. Если 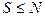, то перейти к пункту 2, иначе - к пункту 4.

4. Конец.

Пример 6. Метод сортировки слиянием. Основной процедурой метода является процедура «слияния» двух упорядоченных массивов

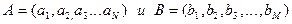
Процедура слияния.

1. Сравниваем начальные элементы двух массивов A и B. Меньший из этих элементов записываем в результирующий массив C, исключив из исходного массива A или B.

2. Если массивы A и B не пусты, то перейти к пункту 1, иначе – к пункту 3.

3. Если один из массивов пуст, то второй приписываем в конец результирующего массива.

Рассмотрим теперь метод слияния, используя процедуру «слияние двух упорядоченных массивов». Для простоты положим .

1. Положить J=0.

2. Разбить массив на пары чисел .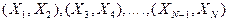

3. Слияния двух следующих друг за другом массивов.

4. J увеличить на 1. Если , то перейти к пункту 3, иначе – конец.

Для алгоритма примера 3 покажите выполнение основных свойств.

Дата добавления: 2014-01-07