Рекурсивные алгоритмы

Рекурсия (от латинского «recurso» - бегу назад, возвращаюсь) в сомом общем виде – это есть правило определения (или построения) некоторого объекта с использованием его же самого.

Рекурсивный алгоритм – это алгоритм, который в качестве выполняемых операций может использовать обращение к самому себе. Рекурсивные алгоритмы представляют собой особый интерес, поскольку зачастую являются более простым и изящным способом решения задачи, чем традиционные алгоритмы. Более детально мы займемся в следующей теме, здесь же рассмотрим несколько примеров.

Пример 7. Вычисление 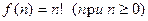с помощью одного из следующих алгоритмов:

a) 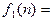если n=0, то 1.

иначе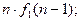

б)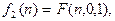

где 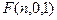= если x = y то z,

иначе .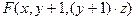

Оба алгоритма вычисляют одно и то же значение, в алгоритме а) значение функции 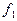определяется через ее же значение, вычисленное на предыдущем шаге; в алгоритме б) значение 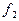определяется с помощью рекурсивно заданной функции F.

Проиллюстрируем работу алгоритма б) для n=4:

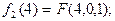
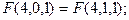
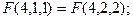
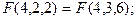
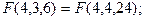
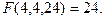
Приведем другие примеры рекурсивных алгоритмов.

Пример 8. Функция «91». Следующий интересный алгоритм при заданном n вычисляет значение, равное 91 для всех 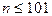и значение n-10 для остальных n.

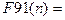если n>100, то n-10,

иначе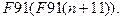

Пример 9. Игра «Ханойская башня».

Имеется 3 основания: A,B,C. На основании A лежат кольца одно га другом в порядке убывания размеров. Необходимо переместить кольца на основание B с использованием «промежуточного» основания C так, чтобы на основании B они тоже лежали в порядке убывания размеров. Единственными разрешенными перемещениями являются такие, при которых кольцо, взятое с вершины одной из пирамид, помещается на большее кольцо либо на пустое основание.

Тем, кто впервые встречается с этой задачей, рекомендуется попробовать решить ее вручную для четырех колец.

Рекурсивный алгоритм игры очень интересен. Обозначим его именем Ханой с параметрами: n – число колец, X – исходное основание, Y – конечное, Z – промежуточное (переменные X,Y,Z могут, например, принимать значения A,B,C). Условимся, что оператор ПЕРЕМЕСТИТЬ(X,Y) выполняет перемещение верхнего кольца с основания X на основание Y.

Алгоритм состоит всего из четырех строк:

Ханой(n, X, Y, Z).

Если n>0, то выполнять 1,2,3.

1. Ханой(n-1, X, Z, Y);

2. ПЕРЕМЕСТИТЬ(X,Y);

3. Ханой(n-1, Z, Y, X);

Выход.

Здесь единственное реальное действие выполняется оператором ПЕРЕМЕСТИТЬ(X,Y).

Число элементарных перемещений, выполняемых этим алгоритмом, составляет 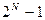. Легенда, связанная с этой древней игрой, гласит, что конец света совпадает с концом перенесения 64-х колец. Соответствующее количество перемещений 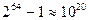; это потребует 10 миллионов лет на сверхбыстродействующей ЭВМ.

Рекомендации по составлению рекурсивных алгоритмов.

Разработка рекурсивного алгоритма обычно состоит из 3-х основных этапов:

а) параметризация. Выделяется одна или несколько переменных, по которым будет производиться рекурсия. Часто это размерность задачи, которая убывает после каждого рекурсивного вызова;

б) поиск простейшего (тривиального) случая и его разрешение. Как правило, это решения задачи при размерности, равной 0 или 1 и т.п.;

в) определение правила сведения задачи размерности n к задаче размерности n-1 с помощью рекурсии. Это правило обычно является основной частью приведенного алгоритма.

Указанные рекомендации, конечно, не являются универсальными, но во многих случаях они помогают, как например, в заданиях на самостоятельную работу.

Лекция 2. РЕКУРСИВНЫЕ ФУНКЦИИ

Рекурсивные функции представляют собой исторически первую формальную модель алгоритма. Они задают алгоритм как правило вычисления значения некоторой числовой функции. Ключевыми в данной теме являются понятия рекурсии и оператор примитивной рекурсии.

Рекурсия в самом общем виде – это есть правило определения (или построения) некоторого объекта с использованием его же самого.

Дадим некоторые важные определения.

Числовые функции, значения которых можно вычислять посредством единого для данной функции алгоритма, называются вычислимыми функциями. Вычислимая функция – интуитивное понятие, поскольку при ее определении использован термин «алгоритм».

Арифметическими называются функции, области определения и значений которых – натуральный ряд.

Арифметические функции с ограниченной областью определения называются частными, остальные – всюду определенными.

Для первоначального ознакомления с рекурсивными функциями рекомендуется литература [ 1,4,8 ]. Для более полного изучения можно воспользоваться монографией А.И. Мальцева [ 5 ] или Р. Петер [ 6 ]. Книга [ 6 ] вместе с тем написана достаточно просто и понятно даже для неподготовленного читателя.

Дата добавления: 2014-01-07