Композиция машины Тьюринга

Определение, функционирование и способы задания машины Тьюринга

Под машиной Тьюринга понимается некоторая гипотетическая (абстрактная) машина, состоящая из следующих частей (рис. 3.1.)

1) бесконечная в обе стороны лента, разбитая на ячейки, в каждой из которых может быть записан только один символ из алфавита , а также пустой символ l;

2) управляющее устройство (рабочей головки), которое в каждый момент времени может находится в одном из состояний из множества 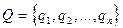. В каждом из состояний головка размещается напротив ячейки и может считывать (обозревать) или записывать в нее букву из алфавита А.

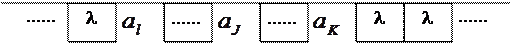Рис. 3.1. Машина Тьюринга

Функционирование МТ состоит из последовательности элементарных шагов (тактов). В каждом шаге выполняются следующие действия:

1. рабочая головка считывает (обозревает) символ ;

2. в зависимости от своего состояния и обозреваемого символа головка вырабатывает символ и записывает его в обозреваемую ячейку (возможно =);

3. головка перемещается на одну ячейку вправо (R), влево (L) или остается на месте (E);

4. головка переходит в другое внутреннее состояние . (возможно =).

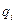Состояние 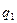называется начальным, - заключительным. При переходе в заключительное состояние машина останавливается.

Полное состояние МТ называется конфигурацией. Это распределение букв по ячейкам ленты, состояние рабочей головки и обозреваемая ячейка. Конфигурация в такте t записывается в виде: , где - подслово слева от обозреваемой ячейки, 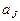- буква в обозреваемой ячейке, - подслово справа.

Начальная конфигурация 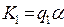и конечная называются стандартными.

Для описания работы МТ существует 3 способа:

- система команд вида

- функциональная таблица;

- граф (диаграмма) переходов.

Рассмотрим их на примерах.

Пример 1. Построить МТ, реализующую конкатенацию двух слов в алфавите . Слова на ленте разделены знаком *. Начальная конфигурация является стандартной.

Система команд МТ имеет вид:

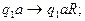В состоянии осуществляется движение головки 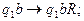вправо до пустого символа.

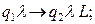
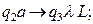Самый правый символ стирается.

Звездочка стирается, если первое слово пустое.

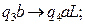Правое слово посимвольно сдвигается влево на одну позицию.

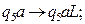
Переход в стандартную конечную конфигурацию.

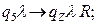
Функциональная таблица

	a	b	*	l
				-
				-
				-
			-

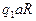
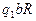
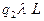
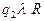
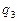
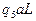
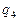
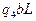
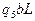
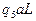
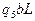
Прочерки в таблице означают, что символ l не может быть встречен в состояниях .

a/aL b/bL

Диаграмма переходов имеет вид:

	a/aR b/bR */*R

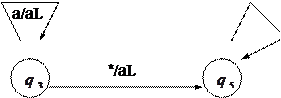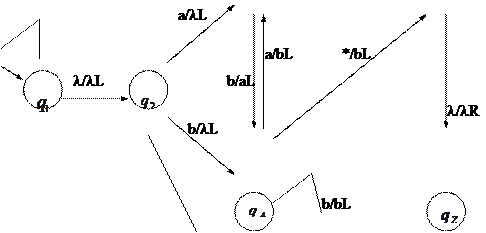стандартная заключительная конфигурация.

Вычисление на МТ словарной функции 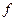будем понимать следующим образом. Пусть в начальной конфигурации на ленте записано слово a. Если значение 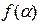определено, то конечного числа шагов (тактов) машина должна перейти в заключительную конфигурацию, в которой на ленте записано слово . В противном случае МТ должна работать бесконечно.

С помощью МТ можно описывать выполнение арифметических операций над числами. При этом числа представляются на ленте как слова в алфавите, состоящем из цифр какой-нибудь системы счисления, и разделяющихся специальным знаком, не входящем данный алфавит, например, *. Наиболее употребительной системой является унарная, состоящего из одного символа –1. 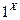Число Х на ленте записывается словом , (или сокращенно ) в алфавите А={1}.

Числовая функция 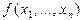правильно вычислима (или просто вычислима) по Тьюрингу, если существует МТ, которая переводит конфигурацию 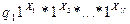в конфигурацию , когда 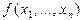= y, или работает бесконечно, когда 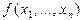не определена.

Пример 2. Операция сложения двух чисел в унарном коде.

Начальная конфигурация:

Конечная конфигурация: т.е. сложение фактически сводится к приписыванию числа b к числу a. Для этого первая 1 стирается, а * заменяется на 1.

Приведем описание МТ в виде функциональной таблицы:

		*	l
			-
			-
		-

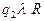
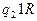
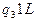
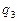
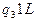
Вышеперечисленные способы описания МТ практически можно использовать только для несложных алгоритмов, т.к. для сложных описание становится слишком громоздким. Точно так же описание рекурсивных функций только с помощью простейших функций и операторов суперпозиции, примитивной рекурсии и минимизации было бы чрезвычайно громоздким. Поэтому примитивная или частичная рекурсивность функции доказывается с использованием других функций, примитивная или частичная рекурсивность которых уже доказана.

Аналогично этому, машины Тьюринга для сложных алгоритмов могут строиться с использованием уже имеющихся МТ. Такое построение называется композицией МТ.

Опишем 4 основных способа композиции МТ:

- последовательная композиция (суперпозиция);

- параллельная композиция;

- разветвление

- цикл

Последовательной композицией машин 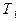и , вычисляющих словарные функции и в алфавите А, называется машина Т, вычисляющая функцию 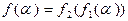. Последовательная композиция изображается следующим образом:

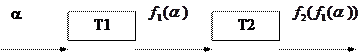и обозначается .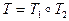

Последовательная композиция используется обычно для описания линейных участков алгоритмов.

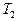Доказательство теоремы о возможности построения машины T, являющейся последовательной композицией двух произвольных машин и осуществляется путем отождествления заключительного состояния с начальным состоянием .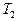

Пример 3. Построить алгоритм умножения 2*Х в унарном коде с использованием машины копирования , переводящей слово a в слово a*a и машины сложения . Искомая МТ выглядит следующим образом:

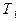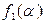Параллельной композицией машин и , вычисляющих словарные функции и 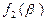в алфавитах А и В соответственно, называется машина Т, вычисляющая словарную функцию . Здесь знак используется для разделения слов при параллельной композиции МТ.

Т

Параллельная композиция МТ 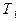и изображается следующим образом:

a

и обозначается: .

Фактически параллельная композиция двух МТ получает на вход слово, состоящее из 2-х слов в разных алфавитах и на выходе выдает слово, состоящее из 2-х слов, т.е. представляет собой две одновременно и независимо работающие машины.

Для реализации параллельной композиции используется машина с двухэтажной лентой. Необходимость в этом вызвана тем, что вычисление 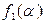и 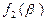во времени происходит последовательно, и 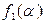, вычисленная, например, первой, может потребовать больше места, чем a, и испортить слово b. Машина с двухэтажной лентой работает следующим образом: слово b переписывается на второй этаж и стирается на первом, вычисляется 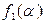на первом этаже, вычисляется 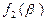на втором этаже и затем переписывается на первый этаж, возможно, со сдвигом.

Для реализации параллельной композиции n машин используется n– этажная лента.

Команда МТ с двухэтажной лентой записывается следующим образом:, где 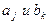- буквы, записанные соответственно на первом и втором этажах.

Пример 4. Реализовать параллельную композицию машин 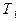и , вычисляющих функции в двоичной системе счисления и a + b в унарной системе.

Входное слово имеет вид: .

Опишем работу МТ системой команд:

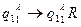
Движение вправо до слова b

Перезапись слова b на второй этаж

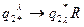
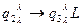
Движение влево до слова a

Прибавление 1 к числу Х.

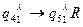
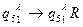
Движение вправо к слову b.

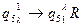
Перепись b на 1-й этаж с одновременным 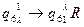сложением чисел a и b.

Стирание младшей 1 в слове b.

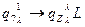
В данном примере реализацию композиции можно было бы осуществить и с одноэтажной лентой, но он служит также для иллюстрации способа построения МТ с двухэтажной лентой.

На конкретных примерах входных данных самостоятельно покажите функционирование описанной МТ в виде последовательности конфигураций.

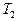Разветвление в композиции МТ. Если заданы машины и , вычисляющие словарные функции и , и машина 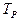, вычисляющая некоторый предикат P(a) с восстановлением (т.е. без стирания слова a), то для реализации разветвления может быть построена машина Т, вычисляющая функцию:

Разветвление машин Тьюринга на схемах композиции изображается следующим образом:

и обозначается , Здесь w - результат работы машины 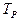, принимающий значения «и» (истина) и «л» (ложь).

Машина Т представляет собой последовательную композицию машин 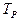и 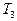; система команд машины 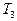имеет вид:

где 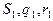- начальные состояния машин соответственно. Команды в фигурных скобках, добавленные к системе команд и 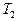, как раз и реализуют передачу управления одной из машин ,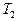по результату работы машины .

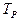Цикл в композиции МТ реализуется по тем же принципам что и разветвление. Циклическим будем считать следующий алгоритм:

«пока P(a)= ’ истина ’, выполнять », где a - слово на ленте перед первым выполнением Т и после очередного выполнения Т.

Для реализации такого цикла используется следующая схема:

Машина выделяет из слова w*a слово a, которое является результатом работы всей композиции при w=л.

Пример 5. Построить композицию МТ для реализации алгоритма умножения двух чисел x и y, заданных в унарном коде.

Для построения композиции вначале составим блок-схему алгоритма (рис 3.2.).

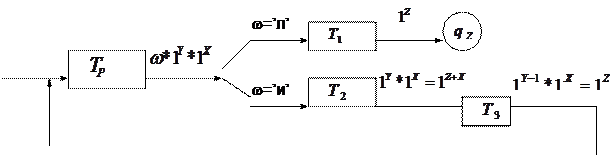Рис 3.3 Композиция МТ, вычисляющая

Здесь 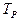- вычисляет с восстановлением предикат ;

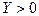- стирает все непустые символы на ленте (Z=0);

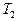- выполняет операцию сложения Z+X в унарном коде;

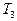- уменьшает Y на 1 (стирает самый левый символ 1);

- конечное состояние всей МТ.

Следует отметить, что во всех случаях в начале алгоритма нужно вставлять проверку исходных данных на особые значения (чаще всего на 0), несоблюдение этого требования может привести к зацикливанию.

Композиция МТ может применяться для построения сложных алгоритмов. Возникает вопрос: всякий ли алгоритм можно реализовать в виде композиции МТ? Ответ на этот вопрос дает Тезис Тьюринга, аналог тезиса Черча: всякий алгоритм может быть реализован с помощью машин Тьюринга и наоборот, всякий процесс, реализуемый машиной Тьюринга, является алгоритмом.

Тезис Тьюринга не является теоремой, доказать его невозможно, т.к. он содержит неформальное понятие «алгоритм». Однако многолетняя математическая практика является надежным подтверждением этого тезиса: за 50 лет не было найдено алгоритма в интуитивном смысле, который нельзя было бы реализовать с помощью машин Тьюринга.

Дата добавления: 2014-01-07