Эквивалентность машин Тьюринга и частично- рекурсивных функций

Эквивалентность МТ и частично-рекурсивных функций означает, что всякая частично-рекурсивная функция оказывается вычислимой по Тьюрингу и наоборот. Приведем примеры реализации на машинах Тьюринга операторов примитивной рекурсии и минимизации.

Пример 6. Построить композицию МТ, вычисляющую в унарном коде функцию, заданную схемой примитивной рекурсии:

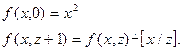
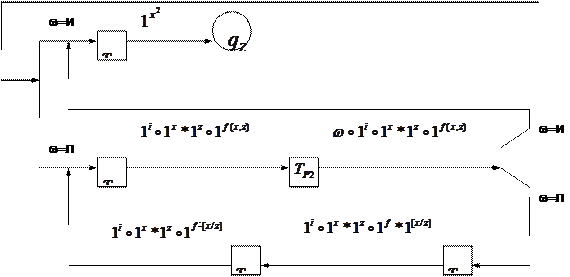
Здесь - копирует исходные данные и ставит маркеры «°»;

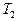- вычисляет функцию ;

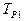- вычисляет предикат z=0;

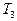- увеличивает i на 1 слева от первого маркера «°»;

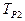- вычисляет предикат i = z;

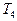- вычисляет функцию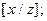

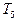- вычисляет функцию ;

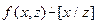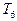- стирает все на ленте слева от второго маркера «°» включительно.

Пример 7. Построить композицию МТ, вычисляющую в унарном коде функцию, заданную оператором минимизации:

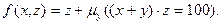
Композиция МТ имеет следующий вид:

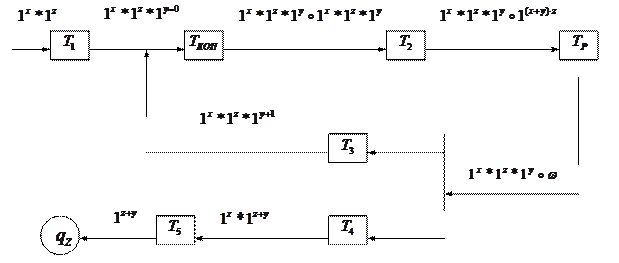Здесь - ставит * после ;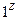

- копирует 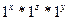для вычисления ;

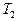- вычисляет ;

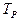- вычисляет предикат (x+y)z=100 без восстановления;

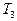- увеличивает y на 1;

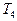- вычисляет z + y;

- стирает все непустые символы на ленте кроме .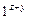

Доказательство того, что всякая функция, вычислимая по Тьюрингу, является частично-рекурсивной, проводится в несколько этапов:

- арифметизация МТ, т.е. сведение символьных данных и операций над строками к целым неотрицательным числам и арифметическим операциям над ними;

- доказательство примитивной рекурсивности операций, выполняемых в одном такте работы МТ;

- доказательство примитивной рекурсивности общего поведения машины (перехода i- го такта к (i+1)-му;

- доказательство частичной рекурсивности конечного результата работы МТ.

Лекция 4. НОРМАЛЬНЫЕ АЛГОРИТМЫ МАРКОВА

Нормальные алгоритмы были предложены в 1951 г. советским ученым А.А. Марковым. Как и машины Тьюринга, нормальные алгоритмы оперируют со словами в некотором алфавите. Главное же их отличие от МТ состоит в том, что нормальный алгоритм представляет собой не устройство, а некоторый упорядоченный набор элементарных операций над словами. Операндами этих операций в общем случае являются последовательности букв, что зачастую упрощает построение нормального алгоритма по сравнению с МТ.

Для изучения данной темы необходимо повторить понятия и определения символьных конструкций и операций над ними (см. Раздел 3.1.).

В литературе алгоритмы Маркова коротко описаны в работах /1,2,5/.

Дата добавления: 2014-01-07