Предназначен для увеличения числа 0 матрицы

Шаг первый: Среди невыделенных элементов матрицы С_к выбирается минимальный элемент h. h>0.

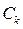Шаг второй: Число h прибавляется ко всем элементам выделенных столбцов и вычитается из всех невыделенных строк матрицы.

Получаем, в которой количество 0 увеличивается хотя бы на один 0.В матрице восстанавливаются звездочки над теми 0 где они были в матрице. И ставится знак "+" над столбцами с независимыми 0. Переход к этапу первому.

Лекция 15. Целочисленное программирование.

Большой класс задач оптимизации сводятся к задачам целочисленного программирования.

Общая особенность таких задач – требование целочисленности решения.

Постановка задачи:

(1)

(2)

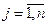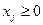, , -целые (3)

Будем называть задачу 1-2 непрерывной задачей линейного программирования (без учета целочисленности).

Рассмотрим возможности применения для задач целочисленного программирования методов линейного программирования.

Пример:

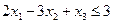
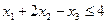
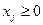, целые

Если решить эту задачу без учета целочисленности, то решение будет следующим:

, , .

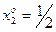Округлим решение:

, , .

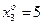3-е ограничение противоречиво; округлим в меньшую сторону:

, , .

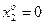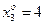1-е ограничение противоречиво.

Таким образом, этот способ неприменим.

Другой особенностью задачи целочисленного программирования является то, что область допустимых решений является невыпуклой и несвязной, а представляет собой систему точек.

Методы отсечения.

Идея всех методов отсечения состоит в следующем:

Сначала решается задача 1-2 без учета целочисленности. Если полученное решение является целым, следовательно оно является оптимальным. Если оно не целочисленное, то вводим дополнительные ограничения, которые отсекают от ОДР нецелочисленную вершину многоугольника допустимых решений. И решение задачи 1-2 повторяется с новыми ограничениями. Процесс ввода дополнительных ограничений проделывается до тех пор, пока не найдется оптимальное целочисленное решение или будет установлено, что решения нет.

Отличие методов отсечения заключается в особенностях формирования дополнительных ограничений для отсечения нацелочисленных решений.

Рассмотрим один из алгоритмов:

Первый алгоритм Гомори.

ОПР: отсечение называется правильным, если оно отсекает от области допустимых решений нецелочисленную точку и не отсекает ни одной целочисленной точки, входящей в состав ОДР.

Геометрически правильное отсечение обозначает некоторую гиперплоскость , которая отсекает от выпуклого многогранника некоторый многогранник, не содержащий целых точек.

ОПР: Дробной частью числа x (обозначается {x}) называется наименьшее неотрицательное число, такое, что разность между числом и его дробной частью есть целое число x-{x}=[x].

Гомори предложил алгоритм, в основе которого лежит двойственный симплексный метод, позволяющий учитывать дополнительные ограничения (правильные отсечения) и состоящий в том, что перебираются псевдопланы, пока не будет получен оптимальный.

Гомори показал, что дополнительные ограничения (правильные отсечения) должны быть сформированы по правилу:

Вводится новая дополнительная переменная

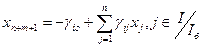, где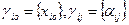

Если по этому правилу ввести ограничение, то оно будет правильным.

Далее задача с новыми ограничениями решается без учета целочисленности двойственным симплексным методом. Если полученное решение не является целочисленным, то вводятся новые ограничения, и процесс повторяется, пока не будет получено оптимальное целочисленное решение.

Алгоритм.

Этап 1.

Используя двойственный симплексный метод, находят оптимальное решение задачи без учета целочисленности. Признаком оптимальности является то, что псевдоплан неотрицательный: .

Если при этом решение целое, то оно является и оптимальным целочисленным решением, иначе

Этап 2.

Формируется правильное отсечение, то есть составляется дополнительное ограничение.

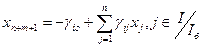(*), где i – номер строки симплексной таблицы, по которой формируется правильное отсечение.

Замечание: сходимость алгоритма повышается, если правильное отсечение сформировать по индексной строке , но формирование по этой строке возможно, если 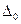нецелое число. В ограничении 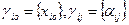(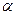- коэффициент разложения).

Этап 3.

В симплексной таблице дополнительно вводится строка и столбец, которые заполняются по следующему правилу:

Все элементы столбца, кроме последнего полагаются =0, а последний элемент =1. элементы строки, соответствующие базисным векторам, полагаются =0, а остальные в соответствии с (*) в столбце псевдоплана записываются , где , в зависимости от того, по какой строке проводится отсечение, остальные элементы строки =, где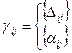

Переход на этап 1.

Так как при выполнении предыдущей итерации все , то в качестве разрешающей строки выбирается последняя строка, которую ввели – строка (в ней отрицательный элемент ).

Замечание: предположим проведено несколько итераций, на каждой мы добавляем новые дополнительные ограничения. Оказывается, что вектор, ранее выведенный из базиса, вновь должен быть в него введен. Тогда выполняются в таблице все необходимые преобразования, но вектор в базис не вводится, из симплексной таблицы вычеркиваются строка и столбец, соответствующие этому вектору. Ввод вторично в базис этого вектора указывает на то, что вводится белее сильное ограничение, которое аннулирует предыдущее.

Такая ситуация встречается довольно часто, следовательно вычеркивание строк и столбцов таблицы позволяет не увеличивать размер двойственной симплексной таблицы.

Лекция 16 нет

Лекция 17. Выпуклое и вогнутое нелинейное программирование.

Пусть задача нелинейного программирования имеет такую постановку:

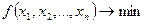
(1)

Предполагается -выпуклые функции.

Такая задача называется выпуклой задачей нелинейного программирования.

ОДР этой задачи, образованная ограничениями, образует ограниченное выпуклое множество. Т.о. задача выпуклого нелинейного программирования заключается в том, чтобы найти min выпуклой функции f на выпуклом множестве, образованном системой ограничений.

Если задача нелинейного программирования имеет постановку:

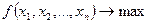
(2)

- вогнутые функции, то задача (2) называется задачей вогнутого нелинейного программирования.

Множество допустимых решений задачи (2) образует также выпуклое множество.

Задача (2) заключается в нахождении max вогнутой функции на выпуклом множестве.

Задачи (1) и (2) эквивалентны, т.е. из (1) можно перейти к задаче (2) и наоборот. Покажем это:

От (1) к (2)

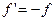
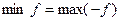
Найти 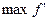т.е.

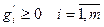
т.о. мы от задачи (1) перешли к задаче (2).

Для решения такого класса задач разработаны методы, которые основаны на основной теореме нелинейного программирования теоремы Куна – Таккера.

Седловая точка функции.

Дата добавления: 2014-01-07