
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №19
|
|
|
|
Пусть задача квадратичного программирования имеет постановку:
 F(x)=CX+XTDX max
F(x)=CX+XTDX max
(1) AX<=B
X>=0
Предположим, что функция строго вогнутая, т.о. будем иметь задачу вогнутого нелинейного программирования.
Применяя теорему Куна-Таккера к задаче (1), можно получить необходимое условия задачи.
Составим функцию Лагранжа для задачи (1):
F(X, Л)=CX+XTDX+Л(B-AX)
dF =C+2DX-ATЛ<=0
dx
dF =b-AX>=0
dЛ
Введем два дополнительных вектора:
V>=0 и W>=0 (2)
С+2DX-AT Л=0 (3)
B-AX-W=0 (4)
Теорема об оптимальности решения:
x10
Вектор X0= x20 <=0 является оптимальным решением
…
xn0
задачи (0)тогда и только тогда, когда существуют такие неотрицательные вектора:
Л=(л1,л2,…лm)>=0
V=(v1,…vn)>=0
W=(w1,…wm)>=0, которые удовлетворяют условиям (3), (4) и условиям дополняющей нежесткости
XTV=0 (5)
ЛTW=0 (6)
Т.о решение задачи квадратичного программирования (1) свелось к нахождению решения системы (n+m) линейных уравнений (3),(4),(5),(6) с (2(n+m)) неизвестными. Решение системы (3-6), если оно существует, то оно должно быть одним из допустимых базисный решений системы (3-4).
Для нахождения ДБР может быть использован обычный симплексный метод.
Алгоритм:
1. Для исходной задачи составляется функция Лагранжа.
2. Записывается условие Куна-Таккера.
3. Вводятся дополнительные вектора (V,W) и записывается система уравнений.
4. Записывается система уравнений в стандартной  форме. Заполняется симплексная таблица, в которой отсутствует строка для целевой функции.
форме. Заполняется симплексная таблица, в которой отсутствует строка для целевой функции.
5. Применяя табличный алгоритм замены переменных, находят базисное решение. Найденное решение проверяется. Если удовлетворяет, то и оптимальным решением. Если неудовлетворяет ищется новое базисное решение и т.д.пока не будет найдено оптимальное решение либо установлено, что несуществует оптимального решения.
Замечание; Решение допустимого базисного решения должно удовлетворять решениям нежесткости. И при замене переменных необходимо менять переменные;

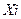
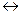 V;
V;
Л 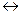 W;
W;
ГЕОМЕТРИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
ГП - это еще один класс задач нелинейного программирования. В ГП как оптимальная функция так и ограничения относятся к позиномиальным функциям.
Позиномом называется функция m переменных вида;
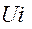 (
(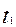
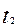 …
…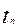 )=
)=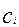 .
.  .
.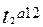 ……
……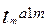 (1)
(1)
где
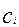
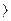 0,
0,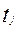
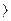 0 j=1,n
0 j=1,n
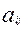 -вещественные числа
-вещественные числа
Задача ГП в общем случае формулируется следующим образом;
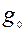 (
(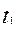
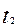 …
…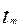 )=
)=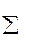



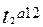
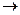 min (2)
min (2)
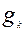 (
(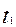
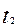 ….
….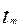 )=
)=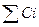

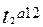 ….
….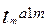

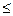 1 (2)
1 (2)
k=1,n-кол-во ограничений
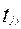 0
0
найти min:
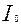 -множество
-множество 
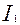 =
=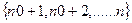
 =
=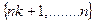
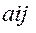 -входящие как в функцию так и в ограничения образуют матрицу экспонент.
-входящие как в функцию так и в ограничения образуют матрицу экспонент.
A=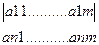

Кол-во столбцов =кол-ву переменных 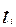
Кол-во строк =кол-ву позиномов, входящих в функцию и в ограничения.
Каждой строке матрицы соответствует один позином.
Функция (1) называется прямой функцией, а ограничения (2)
Называются вынужденными ограничениями.
Лекция 20. Задача геометрического программирования с ограничениями.
Прямая функция:
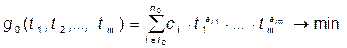 (1)
(1)

где 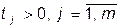
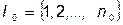
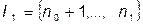
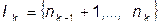
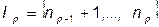
Двойственная задача:
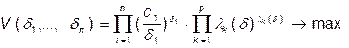 (2)
(2)
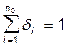 ,
, 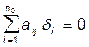 ,
, 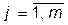 ,
, 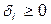 ,
, 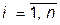 (3)
(3)
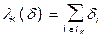 , где
, где 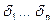 - двойственные переменные;
- двойственные переменные;
число двойственных переменных равно n, а n – это общее число позиномов задачи (1): 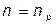
между задачами (1) и (2) имеется соответствие, которое сформулируем в виде теоремы:
Теорема:
1. Если задача (2) имеет оптимальное решение 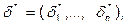 то и задача (1) имеет его
то и задача (1) имеет его 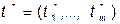 .
.
2. Максимальное значение целевой функции задачи (2) равно минимальному значению целевой функции задачи (1)
3. Оптимальное решение задач (1) и (2) связаны соотношениями:
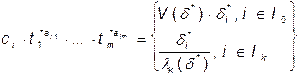
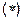
Сформулированная теорема позволяет найти оптимальное решение задачи (1) по найденному задачи (2).
Степень трудности задачи (1) 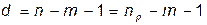
При d=0, решение сводится к решению системы ограничений: 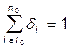 ,
, 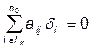 ,
, 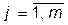 ,
, 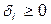
При d>0, используются другие методы (например симплексный)
Алгоритм при d=0
1. По исходной задаче составляется двойственная функция, если без ограничений, то 
2. Cоставляется система уравнений для весовых коэффициентов 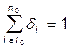 ,
, 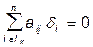 ,
, 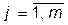 , где
, где 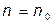 для задачи без ограничений и
для задачи без ограничений и 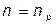
3. Решается система и ищутся 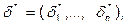
4. Вычисляется значение двойственной функции, при найденном 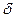
5. Составляется система уравнений для задачи
- без ограничений 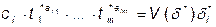
- с ограничениями 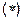
6. Решая полученную систему находят оптимальное решение исходной задачи, при этом
минимальное значение функции будет равно 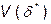
ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ.
Методы этого типа используются для решения задач нелинейного программировании. Они основаны на построении конечной последовательности арифметических действий функций и ограничений задач нелинейного программирования.
Эти методы позволяют найти решение задачи с любой заданной точностью.
Пусть задача нелинейного программирования имеет постановку:
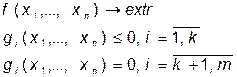
Различают методы:
- если ограничений нет, то задача безусловной оптимизации и соответствующие методы
- если с ограничениями, то задача условной оптимизации и соответственно методы
- одномерной оптимизации, если 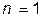
- многомерной оптимизации, если 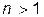
Методы одномерной безусловной оптимизации.
Предположим, что функция 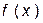 - унимодальная.
- унимодальная.
Определение: Функция 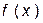 называется унимодальной на
называется унимодальной на 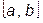 , если существует единственная точка минимума (максимума)
, если существует единственная точка минимума (максимума) 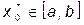 , а отрезок
, а отрезок 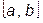 называется интервалом неопределенности.
называется интервалом неопределенности.
Идея поискового метода:
В некоторой точке отрезка 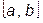 вычисляется
вычисляется 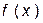 , по результатам сравнения определяется точка, в которой значение функции наименьшее. Отображается т.ж. часть интервала с большим значением.
, по результатам сравнения определяется точка, в которой значение функции наименьшее. Отображается т.ж. часть интервала с большим значением.
На новом интервале операция повторяется и т.д.
Перед началом поиска необходимо задать конечную длину L, которая должна быть не более 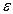 (точность).
(точность).
Метод равномерного поиска:
- Задается начальный отрезок 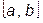 , L,
, L, 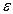
- Затем отрезок 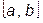 делится n равных частей, вычисляются значения
делится n равных частей, вычисляются значения 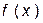 ,
, 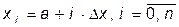
- Значения сравниваются и находится точка 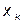 с наименьшим значением функции
с наименьшим значением функции
- Далее интервал 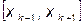 делится на n частей и т.д. пока L>
делится на n частей и т.д. пока L>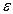
Метод деления на два:
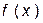

 |

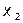
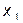
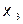
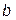
Сравниваем 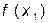 ,
, 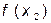 ,
, 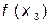 . Интервал неопределенности точками
. Интервал неопределенности точками 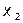 ,
,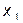 и
и 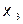 делится на четыре равных отрезка. Вычисляются значения функции в этих точках. Сравниваются полученные значения. В силу унимодальности функции возможны три случая:
делится на четыре равных отрезка. Вычисляются значения функции в этих точках. Сравниваются полученные значения. В силу унимодальности функции возможны три случая:
 |
1. 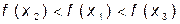 следовательно выбираем отрезок
следовательно выбираем отрезок 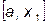
2.  следовательно выбираем отрезок
следовательно выбираем отрезок 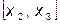






















 3.
3. 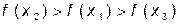 следовательно выбираем отрезок
следовательно выбираем отрезок 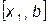

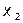
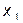
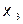
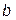

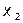
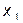
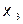
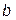

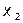
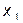
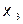
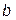
Т.о. интервал неопределенности сократился в двое во всех трех случаях. Далее, на следующей итерации, отрезок снова делится четыре части, но значения функции вычисляются только в двух точках, поскольку значения в трех точках уже были вычислены на предыдущей итерации. Процесс продолжается до тех пор, пока интервал не станет меньше L, т.е. 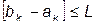 ,
, 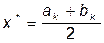 ;
;
Лекция 21. Численные методы условной оптимизации.
Пусть задача нелинейного программирования имеет постановку:
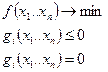
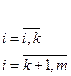
Методы условной оптимизации можно разделить на две группы: прямые и непрямые.
В прямых методах при решении задачи минимизации оперируют непосредственно с исходной задачей. Пример таких методов: метод проекции градиента, метод случайного поиска.
Суть этих методов состоит в том, что строится последовательность точек 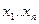 значение функции, на которых убывает
значение функции, на которых убывает 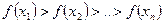 и при этом выполняются ограничения задачи.
и при этом выполняются ограничения задачи.
Непрямые методы сводят исходную задачу условной оптимизации к последовательности задач безусловной оптимизации к некоторой вспомогательной функции. В этих методах ограничения задачи учитываются в неявном виде (косвенно). Пример таких методов: метод штрафных функций.
Прямые методы. Метод случайного поиска.
В его основе лежит внесение элементов случайности в процедуру формирования точек
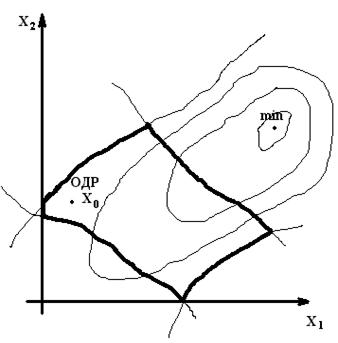
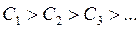
Задаётся начальная точка:
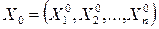

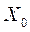 должна
должна 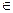 ОДР удовлетворяет всем ограничениями. Затем итерационная процедура построения этих точек.
ОДР удовлетворяет всем ограничениями. Затем итерационная процедура построения этих точек.
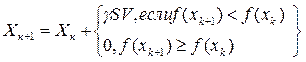
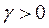 ,шаг поиска это число задаётся
,шаг поиска это число задаётся
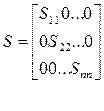 элементы этой матрицы определяются:
элементы этой матрицы определяются: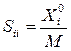 , М – положит большое число.
, М – положит большое число.
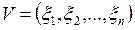 случайный вектор с равномерным распределением на отрезке [-1,1].
случайный вектор с равномерным распределением на отрезке [-1,1].
Равномерный закон распределения.
Возьмем отрезок [-1,1] и разобьём его на 10 частей. И датчиком случайных чисел сгенерировано 100 чисел.
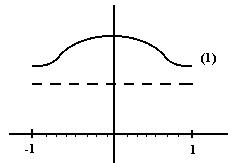 Они будут распределены по равномерному закону. Если для всех К интервал попадет около 10 чисел (может быть 9 или 11).
Они будут распределены по равномерному закону. Если для всех К интервал попадет около 10 чисел (может быть 9 или 11).
Нормальный закон (1).Кривая Гауса.
В результате получаем новую точку Х1. Для новой точки (?) случайным образом получаем новую точку.
Если процессе построения точек некоторая точка выйдет за границы области, то значение компоненты в этой точке полагается равным граничным значениям. Если на какой то итерации делается подряд 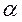 неудачных попыток (
неудачных попыток (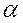 должно быть задано), то после этого шаг поиска
должно быть задано), то после этого шаг поиска 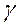 уменьшается в какое то количество раз и т.д.
уменьшается в какое то количество раз и т.д.
Процедуру оптимизации прекращают, если выполняется условие 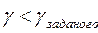 ,
, 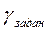 - определяет точность результата.
- определяет точность результата.
Метод проекции градиента.
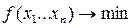 ,
, 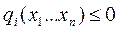
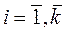
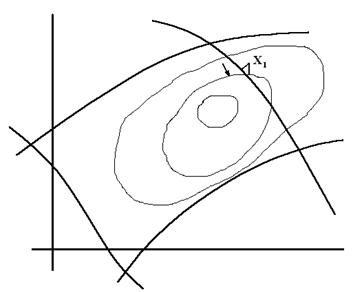
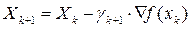
Задаем начальную точку 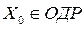 . Потом строиться последовательность точек.
. Потом строиться последовательность точек.
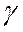 - шаг спуска,
- шаг спуска, 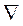 - grad функции в точке Хk.Таким образом, если точка
- grad функции в точке Хk.Таким образом, если точка 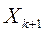 является внутренней точкой, то это обычный градиентный метод.
является внутренней точкой, то это обычный градиентный метод.
Когда точка 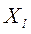 вышла за пределы области, необходимо спроектировать градиент на границу области, а дальше следующая точка ищется в направлении проекции градиента.
вышла за пределы области, необходимо спроектировать градиент на границу области, а дальше следующая точка ищется в направлении проекции градиента.
Определяем новую точку и т.д. Процедура заканчивается, когда

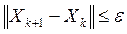 .
.
Сложность метода: построение проекции, если граница нелинейная.
Непрямые методы. Методы штрафных функций.
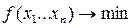
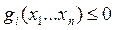
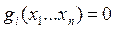
Строим вспомогательную функцию
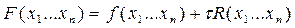
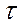 - положительное число – коэффициент штрафа. Штраф за нарушение границы.
- положительное число – коэффициент штрафа. Штраф за нарушение границы.
R – штрафная функция – она подбирается таким образом, что её значение равно нулю внутри области ОДР и резко возрастает за пределами области ОДР.
Метод внутриштрафных функций. (Метод барьерных функций)
Применяется для решения задач без ограничения
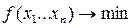
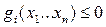
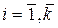
Строится функция F и находится min F
Задача без ограничений (они учитываются косвенно через штрафную функцию)
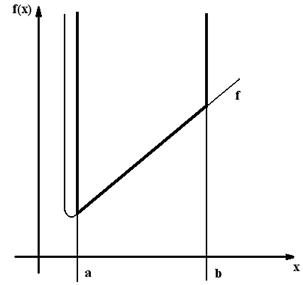 Min F на [a, b], в данном случае он на границе.
Min F на [a, b], в данном случае он на границе.
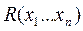 подбирается таким образом, что она равна нулю.
подбирается таким образом, что она равна нулю.
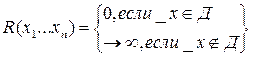
Таким образом, на границе области строится как бы барьер, который препятствует выходу точки за границу. В этом методе штрафуется приближение к границе.
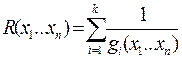
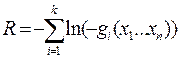
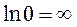
Алгоритм:
Задаётся некоторая последовательность монотонно убывающих чисел, сходящихся к нулю. 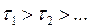 . Задаётся некоторая точка
. Задаётся некоторая точка 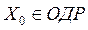 . Затем решается задача безусловной минимизации функции.
. Затем решается задача безусловной минимизации функции.

Метод покоординатного спуска, или наискорейшего спуска.
В результате решения задачи получаем некоторую точку 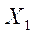 , эта точка используется для безусловной минимизации в качестве начальной, и берем
, эта точка используется для безусловной минимизации в качестве начальной, и берем 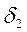 .В результате получаем точку
.В результате получаем точку 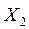 и
и 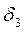 .Получаем последовательность точек
.Получаем последовательность точек 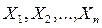 . Это приводит к оптимальному решению задачи
. Это приводит к оптимальному решению задачи 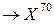
Количество итерации:
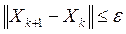
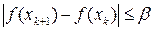
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!