Прогнозирование показателей надёжности при длительном статическом нагружении

Изменение начальных свойств и состояний материалов при дли­тельном статическом нагружении, связанных с относительно высоки­ми температурами, в функции времени, получили название ползуче­сти и релаксации. В предыдущей главе были приведены детермированные графические схемы этих явлений.

Однако, если взять для испытаний однотипные образцы из одно­го и того же материала, но изготовленных их различных партий про­ката на различных станках, то результаты ползучести будет выглядеть примерно так, как это показано на рисунке 4.11.

Здесь пунктиром ограничена область возможных расположения кривых, а сплошной - построенная по средним значениям.

Наиболее полное представление о ползучести даёт закон распре­деления для каждого из значений 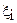. Если этот закон выражен анали­тической моделью (нормального показательного или другого распре­деления), то наиболее полная информация о надёжности (долговечности) изделия содержится в установленном виде закона распределе­ния и зависимости параметров этого закона от уровня деформации.

Рисунок 4.11 – Схемы испытания образцов на ползучесть

Например, в случае нормального закона распределения плот­ность вероятности определится:

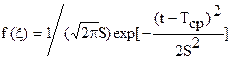
где S – среднее квадратичное отклонение,

T_cp – математическое ожидание или центр рассеивания.

Для определённого числа опытов:

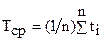
где n - количество испытаний.

Таким образом, надёжность объекта будет полностью определе­на, когда задан закон распределения и характеристики распределе­ния. Однако в справочной литературе приводятся только средние зна­чения характеристик ползучести и релаксации. К тому же в реальных условиях, как параметры распределения, так и законы, зависит от многих факторов, и установление этих зависимостей статистическими методами (путём проведения испытаний) практически не возможно.

Поэтому информация о ползучести и релаксации, а также уста­лости, в том виде, каком она представлена в литературе, не может быть непосредственно использована для получения вероятностных оценок надёжности. В связи с этим используют формализованную физическую модель с вероятностной интерпретацией.

В этом случае основным показателем надёжности служит показа­тель долговечности - срок службы (наработки) до отказа Т, а прогно­зирование ведёт по кинетическим закономерностям.

При конструировании изделий ищут связь между долговечно­стью и напряжением. Эта связь для пластмасс и полимерных мате­риалов выражается экспоненциальным законом:

T_r=A e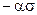

Где А, 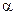- константы, определяемые опытным путём;

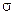– заданное напряжение.

В этом случае необходимо уметь по заданной долговечности оп­ределить допускаемые напряжения материала.

Для этой цели с достаточной для практических расчётов точно­стью можно рекомендовать следующие упрощённые формулы:

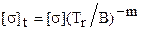
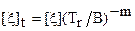
где [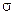]_t и [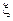]_t – соответственно допускаемые напряжения и де­формации пластмассовой детали при длительном статическом нагружении в течении Т часов.

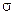[] и [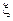] – допускаемые расчётные напряжения и деформации при кратковременном статическом нагружении;

m, В – константы, учитывающие природу пластмасс.

Константы для фторопласта имеют следующие значения:

m= 0,062, В = 3,3 х10^-4, а для полиэтилена m = 0,04, В = 1х10^-5

В виду сложности явления ползучести для металлов предложены многочисленные формулы, полученные на основании эксперимен­тальных данных. Обычно эти формулы не дают удовлетворительного результата на всём интервале и носят частный характер, показывая относительно удовлетворительное совпадение только на некоторых небольших участках кривых ползучести.

Для неустановившейся ползучести применяется следующая зави­симость между скоростью ползучести и напряжением:

V_n = К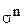

Где V_n – скорость ползучести;

К и n – коэффициенты, зависящие от температуры испытания и свойств материалов.

Для углеродистой стали, например, значения коэффициентов n, К следующие: n = 6,35; К = 0,17 х 10^-20.

При 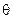° = 427; n = 3,1; К = 0,26 х 10^-12 при 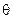° = 593 и т.д.

Расчётное условие при пренебрежении упругой деформации имеет вид:

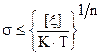
Где [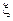] – допускаемая деформация за время службы конструкции;

В тех случаях, когда деформация ползучести не играет роли, а деталь работает под напряжением при высокой температуре, тогда расчёты упрощаются. При этом допускаемое напряжение находят в зависимости от предела длительной прочности:

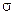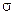[] = _д/n_д

где 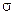_д – предел длительной прочности (обычно время испытания 10000 или 100000 ч); n_д – коэффициент запаса прочности (n_д > 1,5).

Пределом длительной прочности называют отношение нагрузки к начальной плошали поперечного сечения образца, под действием, которой образец доводится до разрыва за определённый промежуток времени при заданной температуре.

В тех случаях, когда важным условием является ограничение деформации детали при известной скорости ползучести, тогда расчёт ведут приближённо:

V_nT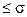/Е, где 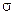- рабочее напряжение.

Очевидно, это условие будет выполнено, если .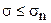

Где а_n - предел ползучести, отнесённый к скорости ползучести.

При расчёте деталей, работающих в условиях релаксации, необ­ходимо определить напряжение через заданное время наработки, а за­тем по графикам изменения напряжений находят начальное напряже­ние .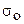

4.9 Прогнозирование показателей надёжности по критерию ус­талостной прочности.

В качестве основных характеристик сопротивления усталости принимают кривые усталости, которые получают путём испытания стандартных образцов. При рассмотрении вопросов физики отказов, была приведена одна из таких кривых усталости. Считая, что между напряжением и числом циклов существует функциональная связь. В действительности, при получении кривых усталости наблюдается разброс или рассеивание, как показано на рисунке 4.12.

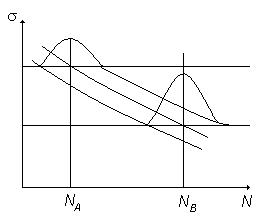
Рисунок 4.12 – Схема семейства кривых усталости.

Относительно прогнозирования долговечности деталей, рабо­тающих при многоцикловой нагрузке, можно сказать то же самое, что и о прогнозировании показателей надёжности при длительном статическом нагружении. Показателем надёжности объекта устанав­ливается на основании напряжений и коэффициентов, учитывающих концентрацию напряжений и др. факторы.

Расчёт на выносливость производится для опасных сечений при этом определяют запасы прочности по нормальным 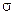(удлинение) и тангенциальным 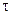(скручивание на валах) напряжениям, например, для симметричных циклов.

.

.

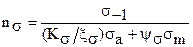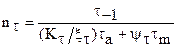Общий запас прочности:

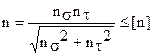
где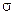 К, К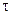- коэффициенты, учитывающие концентрации напря­жений;

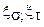- коэффициенты, учитывающие влияние размеров де­талей на предел выносливости;

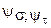- коэффициенты, характеризующие чувствительность материала к не симметрии цикла;

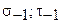- табличные значения напряжения усталости при цик­лических нагрузках.

Обычно коэффициент запаса находится в пределах 2,3 - 5,0.

Дата добавления: 2014-01-07