Прогнозирование показателей надёжности по критерию из­носа

Анализ большого исследований износа многих материалов в раз­личных условиях трения показывает, что износ в зависимости от сро­ка службы изделия определяется зависимостью:

U = KP^mlV^m2t

Где m₁,m₂ - экспериментальные коэффициенты;

К - коэффициент, оценивающий износостойкость материа­ла.

При известных значениях m_1,m₂ результаты расчёта износа при единственной реализации процесса не смогут объективно характери­зовать изучаемый объект. Это связано с тем, что изделие может по­пасть в различные условия эксплуатации и работать при различных режимах. Величины К, Р, V, приведённый функциональной зависи­мости являются случайными и зависят от большого числа факторов. В связи с этим нельзя точно предсказать проведение системы, а можно лишь определить вероятность того или иного её состояния. При такого подходе зависимость представляет собой поведение сложной системы.

Для прогнозирования показателей надёжности сложной системь: используется имитационный метод статистического моделирования который получил название метода Монте - Карло. Особенность этогс метода заключается в многократном расчёте параметров по принятой математической модели.

При этом для случайных параметров перебираются большое чис­ло вероятных их значений в соответствии с законами их распределе­ния. В результате каждое статистическое "испытание" является од­ной из реализаций случайного процесса, так как представляя зафик­сированное значение аргументов, получаем детерминированную за­висимость, которая описывает данный процесс при принятых усло­виях.

В результате многократных реализаций, получаем большое чис­ло значений случайного процесса, а соответственно с этим и его ос­новные параметры.

Рассмотрим простейший случай расчёта надёжности изделия, математическая модель износа которого описана уравнением, а схема формирования отказа приведена на рисунке 4.13.

Рисунок 4.13 - Схема формирования постепенного отказа.

В данном случае К P^mlV^m2 – это скорость изменения параметра X = F(U). Из анализа работы изделия установлено, что предельно допустимое значение параметра равно Х_мах. При U = Х_тах наступает предельное состояние, которое определяет срок службы изделия до отказа t = Т. Срок службы является функцией случайного аргумента V, т.е.

Т = 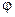(V) = x_max/V = X_max/ (К P^mlV^m2)

Средний срок службы изделия, при прямолинейной зависимости составляет:

T_ср = X_max/V_ср,

а вероятность безотказной работы описывается уравнением (модель формирования постепенного отказа):

P(t) = 0,5 + Ф[(Х_тах - V_cpT) / (Т 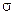_х)]

Где V_cp – математическое ожидание;

а_х – среднеквадратичное отклонение скорости процесса;

Ф – нормированная функция Лапласа (для её определения необходимо определить численное значение величины в квадратных скобках, а затем по таблицам находят Ф.

На рисунке 4.17 приведена упрощённая блок – схема алгоритма надежности ичпепия на ЭВМ.

Рисунок 4.14 – Блок – схема алгоритма для расчёта надёжности методом Монте - Карло.

В ней, в правой части, приведены законы распределения нагрузок f(P), скоростей f(V) и условий эксплуатации f(K) (взятых произвольно).

Задача заключается в том, чтобы определить вероятность безотказной работы изделия.

Алгоритм для оценки надёжности состоит из программы одного случайного испытания, в результате которого определяется конкретное значение скорости изменения параметра V_x (оператор 4). Данное испытание повторяется N раз. Причём, чем больше N, тем надёжнее результаты (обычно N 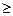50).

Последовательность статистического испытания следующая.

После ввода необходимых данных (оператор 1) производится выбор конкретных для данного испытания значений Р, V, К (оператор 2) и производится расчёт процесса повреждения V (оператор 3) и конкретное значение параметра V_x

(оператор 4) засы­лается во внешнюю память. Данная процедура повторяется N раз. Заметим, что для выбора конкретного значения каждого из парамет­ров с учётом их распределения, применяется генератор случайных чисел, при помощи которого выбирается данное случайное число. После накопления статистических данных (при n = W) производится определение характеристик случайных величин:

V_cp и 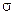_х (операторы 6 и 7), а затем и вероятность безотказной работы (оператор 8) изделия.

Полученные данные могут быть использованы также для построения гистограммы V_k или наработок до отказа Т_i.

Дата добавления: 2014-01-07