
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 7
|
|
|
|
Теорема 6.
Теорема 5.
Дисперсия неслучайной величины равна нулю.
D(C)=0
D(C)=M((C-M(C))2)=M((C-C)2)=M(02)=0
Неслучайную величину можно выносить за знак дисперсии, если предварительно возвести в квадрат.
D(CX)=C2D(X)
D(CX)=M((CX-M(CX))2)=M((CX-CM(X))2)=M(C2(X-M(X))2)=C2M((X-M(X))2)=C2D(X)
Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс два их корреляционных момента.
D(X+Y)=D(X)+D(Y)+2kxy
D(X+Y)=M((X+Y-M(X+Y))2)=M((X+Y-( +
+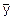 ))2)=M(((X-
))2)=M(((X- )+(Y-
)+(Y-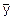 ))2)=M((X-
))2)=M((X- )2+2(X-
)2+2(X- )(Y-
)(Y-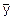 )+(Y-
)+(Y-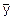 )2)=
)2)=
=M((X- )2)+2M((X-
)2)+2M((X- )(Y-
)(Y-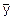 ))+M((Y-
))+M((Y-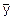 )2)=D(X)+2kxy+D(Y)
)2)=D(X)+2kxy+D(Y)
Если величины X и Y независимы, то kxy=0 D(X+Y)=D(X)+D(Y)
D(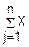 j)=
j)=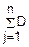 (Xj)+2
(Xj)+2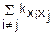
Если величины X1, X2…Xn независимы, то D(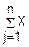 j)=
j)=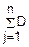 (Xj)
(Xj)
Теорема 8. Математическое ожидание и дисперсия биномиального распределения.
Пусть X – дискретная случайная величина, распределенная по биномиальному закону, т. е. X=0, 1…n p(X=m)=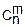 •pm•(1-p)n-m
•pm•(1-p)n-m
Случайную величину X можно рассматривать как число успехов в серии из n испытаний Бернулли, если в каждом испытании успех происходит с вероятностью p, а а неудача с вероятностью q=(1-p).
Свяжем с испытанием Бернулли под номером j случайную величину Xj=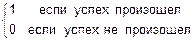 .
.
p(Xj=1)=p
p(Xj=0)=q
M(Xj)=1•p+0•q=p
D(Xj)=(1-p)2•p+(0-p)2q=q2p+p2q=pq(p+q)=pq
X=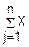 j, т. к. X1, X2…Xn независимы.
j, т. к. X1, X2…Xn независимы.
M(X)=M(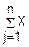 j)=
j)=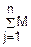 (Xj)=
(Xj)=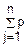 =np
=np
D(X)=D(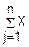 j)=
j)=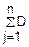 (Xj)=
(Xj)=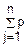 q=npq
q=npq
1. Плотность вероятности известной функции случайной величины.
Пусть X – непрерывная случайная величина.
Y=φ(X), где φ – некоторая известная функция.
Пусть известны Fx(x) и fx(x). Требуется определить Fy(y) и fy(y).
Пусть y=φ(x) монотонно возрастает.
По теореме о существовании, непрерывности и монотонности обратной функции для функции y=φ(x) существует обратная функция x=ψ(y)=φ-1(y), которая также будет монотонно возрастать.
Fy(y)=p(Y<y)
A={Y<y}
B={X<x=ψ(y)}
A=B
p(A)=p(B)
p(Y<y)=p(X<x=ψ(y))=Fx(ψ(y))
Fy(y)=Fx(ψ(y))
Пусть y=φ(x) монотонно убывает.
По теореме о существовании, непрерывности и монотонности обратной функции для функции y=φ(x) существует обратная функция x=ψ(y)=φ-1(y), которая также будет монотонно убывать.
A={Y<y}
B={X<x=ψ(y)}
A=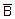
p(A)=p(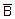 )=1-p(B)
)=1-p(B)
p(Y<y)=1-p(X<x=ψ(y))=1-Fx(ψ(y))
Fy(y)=1-Fx(ψ(y))
fy(y)=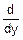 Fy(y)=
Fy(y)=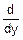
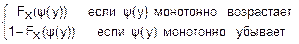 =
=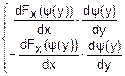 =
=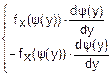
fy(y)=fx(ψ(y))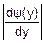 (*)
(*)
Если функция y=φ(x) является кусочно-монотонной, то нужно область определения этой функции разбить на участки, на которых функция y=φ(x) является строго монотонной, для каждого из участка применить формулу (*),а потом просуммировать все полученные выражения.
fy(y)=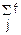 x(ψj(y))
x(ψj(y))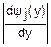
Теорема.
Линейная функция нормальной случайной величины является нормальной случайной величиной.
Y=aX+b
fx(x)=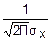 exp(-
exp(-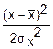 ) при xÎ(-∞; +∞)
) при xÎ(-∞; +∞)
M(Y)=M(aX+b)=aM(X)+b=a +b=
+b=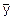
D(Y)=D(aX+b)=D(aX)+D(B)=a2D(X)+0=a2σx2=σy2; σy=|a|σx
X=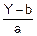
x=ψ(y); ψ(y)=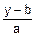
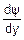 =
=
fy(y)=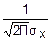 exp(-
exp(-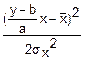 )
)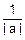 =
=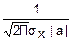 exp(-
exp(-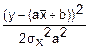 )=
)=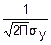 exp(-
exp(-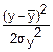 ) – нормальный закон распределения.
) – нормальный закон распределения.
Справедливо более общее утверждение: Линейное преобразование, примененное к случайной величине, не меняет характера распределения этой случайной величины.
2. Плотность распределения функции нескольких случайных аргументов.
Пусть имеется система непрерывных случайных величин (X1, X2…Xn) и некоторая известная функция Z=φ(X1, X2…Xn) (1).
Пусть плотность вероятности системы (X1, X2…Xn) известна. Требуется определить плотность вероятности fz(z).
p(z≤Z<z+dz)=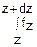 (z)dz=
(z)dz=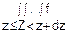 (x1, x2…xn)dx1dx2…dxn (2)
(x1, x2…xn)dx1dx2…dxn (2)
В соответствии с теоремой о среднем значении, интеграл, стоящий в левой части соотношения (2) равен fz(z)dz.
Для вычисления интеграла, стоящего в правой части, перейдем к новым координатам.
Будем считать, что уравнение (1) разрешимо относительно одной из переменных X1, X2…Xn. Пусть
X1=ψ(X2, X3…Xn, Z)
В качестве новой системы координат возьмем
x2=x2
x3=x3
……
xn=xn
x1=z
В соответствии с правилами замены переменных в кратном интеграле, домножим на якобиан перехода от одной системы координат к другой.
При этом Z изменяется в пределах от z до z+dz.
С учетом этого, соотношение (2) принимает вид
fz(z)dz=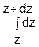
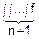 (ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn=|по теореме о среднем значении|=
(ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn=|по теореме о среднем значении|=
=fz(z)dz=dz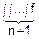 (ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn
(ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn
fz(z)=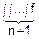 (ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn
(ψ(x2, x3…xn, z), x2…xn)|J|dx2dx3…dxn
Композиция законов распределения.
Пусть Z=X+Y – композиция случайных величин. Пусть известна плотность вероятности f(x, y). Требуется вычислить fz(z).
В соответствии с (2)
fz(z)dz=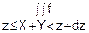 (x, y)dxdy=
(x, y)dxdy=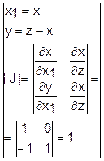 =
=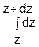
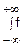 (x, z-x)dx
(x, z-x)dx
fz(z)dz=dz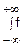 (x, z-x)dx
(x, z-x)dx
fz(z)=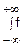 (x, z-x)dx (3)
(x, z-x)dx (3)
fz(z)=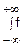 (z-y, y)dy (4)
(z-y, y)dy (4)
Если X и Y – независимые случайные величины, то f(x, y)=fx(x)•fy(y)
fz(z)=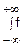 x(x)•fy(z-x)dx=
x(x)•fy(z-x)dx=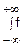 x(z-y)•fy(y)dy (5)
x(z-y)•fy(y)dy (5)
(3), (4), (5) – композиция законов распределения (свертка законов распределения).
Композиция двух равномерных законов распределения (закон треугольника, закон Симпсона).
Пусть Z=X+Y
X и Y – независимые случайные величины
f(x, y)=fx(x)•fy(y)
fx(x)=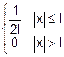
fy(y)=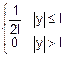
fz(z)=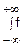 x(x)•fy(z-x)dx=
x(x)•fy(z-x)dx=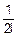
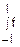 y(z-x)dx
y(z-x)dx
fy(z-x)=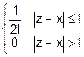
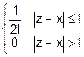 Û
Û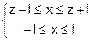 Û
Û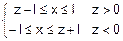
fz(z)=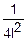
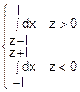 =
=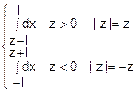 =
=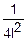 •(2l-|z|) fz(z)=
•(2l-|z|) fz(z)=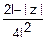
3. Распределение χ2.
Пусть имеется n случайных величин ξ1, ξ2…ξn, обладающих следующими свойствами
Все эти величины центрированы, т. е. M(ξj)=0
Все эти величины нормированы, т. е. D(ξj)=1
Все эти величины независимы, т. е. f(ξ1, ξ2…ξn)=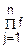 j(ξj)
j(ξj)
Все эти величины имеют нормальный закон распределения, т. е. fj(ξj)=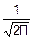 exp(-
exp(-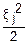 )
)
Рассмотрим χn2=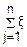 i2
i2
χn=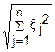
n – число степеней свободы.
Можно показать, что плотность вероятности случайной величины χn будет иметь вид
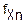 (χn)=
(χn)=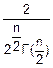 exp(-
exp(-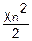 )χnn-1 (1)
)χnn-1 (1)
Γ(p)=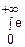 -ptp-1dt (сходится для всех p>0)
-ptp-1dt (сходится для всех p>0)
Получим закон распределения z=χn2
χn=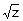
fz(z)=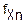 (
(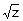 )•
)•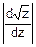 =
=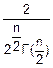 •exp(-
•exp(-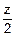 )•
)•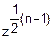 •
•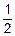 •
•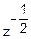
fz(z)=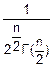 •exp(-
•exp(-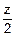 )•
)•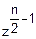 (2)
(2)
Формулы (1) и (2) используются, если число степеней свободы n≤30. Если число степеней свободы больше, чем 30, то χ-распределение и χ2-распределение не отличаются от нормального закона распределения.
4. Закон распределения Стьюдента.
Пусть имеется n+1 случайных величин ξ0, ξ1…ξn, обладающих следующими свойствами
Все эти величины центрированы, т. е. M(ξj)=0
Все эти величины нормированы, т. е. D(ξj)=1
Все эти величины независимы, т. е. f(ξ1, ξ2…ξn)=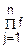 j(ξj)
j(ξj)
Все эти величины имеют нормальный закон распределения, т. е. fj(ξj)=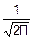 exp(-
exp(-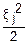 )
)
Закон распределения Стьюдента Tn=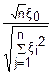 =
=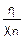
Используя описанную ранее схему (получения плотности вероятности нескольких случайных величин) можно получить
f(tn)=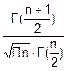 •(1+
•(1+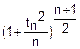 )
)
n – число степеней свободы.
При n>30 закон распределения Стьюдента не отличается от нормального.
5. Характеристическая функция системы случайных величин и ее свойства. (БИЛЕТ № 21)
Пусть имеется система двух случайных функций X и Y. Характеристической функцией этой системы называется функция двух переменных E(u1, u2)=M(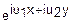 ).
).
E(u1, u2)=M(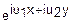 )=
)=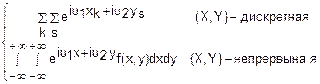
E(u1, 0)=M(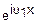 )=Ex(u1)
)=Ex(u1)
E(0, u2)=M(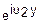 )=Ey(u2)
)=Ey(u2)
Пусть X и Y – независимые случайные величины. Тогда
E(u1, u2)=M(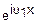 •
•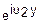 )=M(
)=M(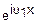 )•M(
)•M(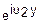 )=Ex(u1)•Ey(u2)
)=Ex(u1)•Ey(u2)
f(x, y)=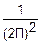
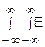 (u1, u2)
(u1, u2)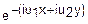 du1du2
du1du2
mks=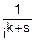
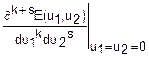
mks=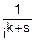
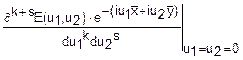
Глава 5. Предельные теоремы теории вероятностей.
Эти теоремы делят на два класса – закон больших чисел и центральные предельные теоремы.
Закон больших чисел устанавливает условия, при которых случайную величину можно считать неслучайной. К закону больших чисел относятся теорема Чебышева, теорема Бернулли, теорема Хинчина.
К центральной предельной теореме относятся центральная предельная теорема Ляпунова и теорема Муавра-Лапласа.
1. Неравенство Чебышева.
Пусть имеется случайная величина X, с математическим ожиданием M(X)= и дисперсией D(X).
и дисперсией D(X).
Тогда справедливо неравенство Чебышева
"(ε>0) p(|X- |≥ε)≤
|≥ε)≤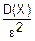
Доказательство.
Пусть X – непрерывная случайна величина. Тогда
p(|X- |≥ε)=
|≥ε)=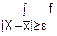 (x)dx (1)
(x)dx (1)
|X- |≥ε
|≥ε
(X- )2≥ε2
)2≥ε2
1≤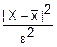
f(x)≤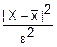 ·f(x) (f(x)≥0)
·f(x) (f(x)≥0)
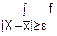 (x)dx≤
(x)dx≤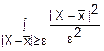 f(x)dx≤
f(x)dx≤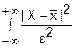 f(x)dx=
f(x)dx=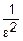 D(x) (2)
D(x) (2)
Подставив (2) в (1), получим неравенство Чебышева.
Пусть X – дискретная случайна величина с рядом распределения
| X | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Тогда
p(|X- |≥ε)=
|≥ε)=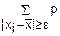 i (3)
i (3)
|xi- |≥ε
|≥ε
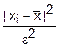 ≥1
≥1
pi·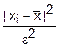 ≥pi
≥pi
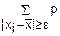 i≤
i≤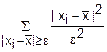 pi≤
pi≤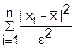 pi=
pi=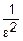 D(x) (4)
D(x) (4)
Подставив (4) в (3), получим неравенство Чебышева.
2. Теорема Чебышева.
Пусть имеется последовательность случайных величин X1, X2…Xn, обладающих следующим свойствами
Все эти величины независимы в совокупности.
Все эти величины имеют конечные математические ожидания M(Xj)= j (j=1, 2…n).
j (j=1, 2…n).
Все эти величины имеют ограниченные дисперсии, т. е. $σ02 D(Xj)≤σ02 (j=1, 2…n).
Тогда среднее арифметическое этих случайных величин по вероятности сходится к среднему арифметическому математических ожиданий этих величин, т. е. выполняется соотношение
"(ε>0) 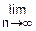 p(|
p(|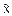 -
- |≥ε)=0
|≥ε)=0
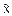 =
=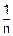
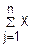 j
j
 =
=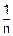
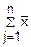 j
j
Доказательство.
Воспользуемся неравенством Чебышева, положив в этом неравенстве X=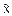 .
.
M(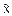 )=M(
)=M(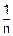
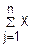 j)=
j)=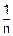 M(
M(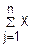 j)=
j)=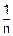
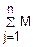 (Xj)=
(Xj)=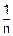
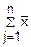 j=
j=
D(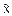 )=D(
)=D(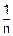
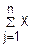 j)=
j)=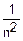 D(
D(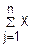 j)=|величины независимы|=
j)=|величины независимы|=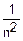
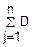 (Xj)≤
(Xj)≤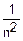
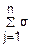 02=
02=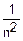 ·n·σ02
·n·σ02
D(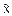 )≤
)≤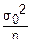
0≤p(|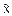 -
- |≥ε)≤
|≥ε)≤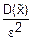 ≤
≤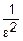
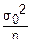 (1)
(1)
Переходя в неравенстве (1) к пределу при n→∞, получим
"(ε>0) 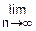 p(|
p(|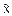 -
- |≥ε)=0
|≥ε)=0
3. Теорема Бернулли.
Пусть проводится серия из n испытаний Бернулли, т. е. проводится серия из n независимых испытаний, в каждом их которых некоторое событие может произойти с одной и той же вероятностью p. Тогда частота появления этого события по вероятности сходится к вероятности появления этого события в каждом испытании, т. е. к p.
p*(A)=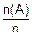
"(ε>0) 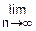 p((p*(A)-p)≥ε)=0
p((p*(A)-p)≥ε)=0
Доказательство.
С каждым их испытаний Бернулли свяжем случайную величину Xj, которая может принимать два значения: 1, если событие A в испытании с номером j произошло (вероятность этого p), и 0 в противном случае (вероятность этого q=1-p). (j=1, 2…n)
Величины X1, X2…Xj независимы (т. к. испытания независимы).
M(Xj)=1·p+0·q=p – все величины имеют конечные математические ожидания.
D(Xj)=(1-p)2·p+(0-p)2·q=q2p+p2q=pq(p+q)=pq=p(1-p)≤p-p2+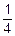 -
-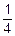 =
=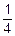 -(
-(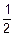 -p)2≤
-p)2≤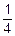 - все величины имеют ограниченные дисперсии.
- все величины имеют ограниченные дисперсии.
Все условия теоремы Чебышева выполнены.
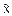 =
=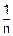
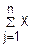 j=
j=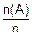 =p*(A)
=p*(A)
M(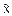 )=M(
)=M(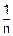
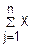 j)=
j)=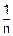 ·np=p
·np=p
Воспользовавшись теоремой Чебышева, получим
"(ε>0) 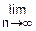 p((p*(A)-p)≥ε)=0
p((p*(A)-p)≥ε)=0
4. Теорема Хинчина.
Пусть имеется последовательность случайных величин X1, X2…Xn, обладающих следующим свойствами
Все эти величины независимы в совокупности.
Все эти величины имеют одинаковый закон распределения.
Все эти величины имеют конечное математическое ожидание M(Xj)=
Тогда по вероятности среднее арифметическое этих величин сходится к их математическому ожиданию  .
.
Доказательство.
Y=
Ey(u)=M(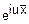 )=
)=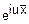
Для доказательства теоремы достаточно показать, что характеристическая функция среднего арифметического этих случайных величин при n→∞ стремится к 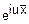 .
.
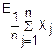 (u)=
(u)=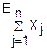 (
(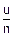 )=
)=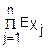 (
(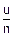 )=|закон распределения одинаков|=(
)=|закон распределения одинаков|=(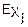 (
(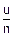 ))n
))n
Разложим (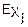 (
(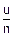 ))n в ряд Маклорена.
))n в ряд Маклорена.
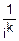
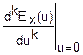 =mk
=mk
(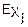 (
(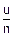 ))n=(Ex(
))n=(Ex(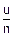
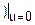 +
+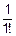
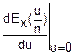 ·u+
·u+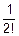
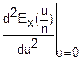 ·u2+…)n=(1+i·
·u2+…)n=(1+i·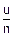
 -
-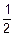 m2(
m2(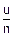 )2+…)n=(1+
)2+…)n=(1+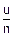 (i
(i +o(
+o(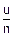 )))n
)))n
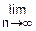
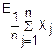 (u)=
(u)=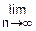 (1+
(1+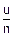 (i
(i +o(
+o(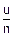 )))n=
)))n=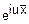
Теорема доказана.
3. Центральные предельные теоремы.
Теорема Ляпунова.
Пусть имеется последовательность случайных величин X1, X2…Xn, удовлетворяющих следующим условиям
Величины X1, X2…Xn независимы.
Величины X1, X2…Xn обладают конечными абсолютными центральными моментами третьего порядка, т. е. M(|Xj-M(Xj)|3) удовлетворяет условию 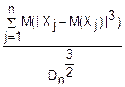 →0 при n→∞. Dn=D(
→0 при n→∞. Dn=D(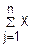 j)
j)
Тогда при n→∞ случайная величина Zn=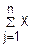 j имеет нормальный закон распределения.
j имеет нормальный закон распределения.
Теорема Ляпунова для одинаково распределенных случайных величин.
Пусть имеется последовательность случайных величин X1, X2…Xn, обладающих следующим свойствами
Величины X1, X2…Xn независимы.
Величины X1, X2…Xn одинаково распределены.
Величины X1, X2…Xn имеют конечное и одинаковое математическое ожидание M(Xj)=
Величины X1, X2…Xn имеют конечную и одинаковую дисперсию D(Xj)=σ2
Тогда при n→∞ случайная величина Zn=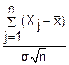 имеет нормальный закон распределения, причем M(Zn)=0 и D(Zn)=1
имеет нормальный закон распределения, причем M(Zn)=0 и D(Zn)=1
Доказательство.
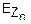 (u)=exp(-
(u)=exp(-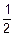 u2)
u2)
Для доказательства покажем, что характеристическая функция Zn при n→∞ стремится к exp(-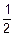 u2).
u2).
Введем случайную величину Yj=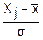
M(Yj)=M(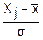 )=
)=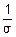 M(Xj-
M(Xj- )=
)=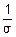 (M(Xj)-M(
(M(Xj)-M( ))=
))=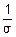 (
( -
- )=0 – т. е. Yj центрированы.
)=0 – т. е. Yj центрированы.
D(Yj)=D(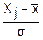 )=
)=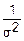 D(Xj-
D(Xj- )=
)=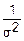 (D(Xj)-D(
(D(Xj)-D( ))=
))=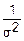 (σ2-0)=1 – т. е. Yj нормированы.
(σ2-0)=1 – т. е. Yj нормированы.
Тогда Zn=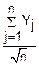
M(Zn)=M(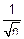
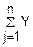 j)=
j)=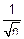
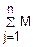 (Yj)=0
(Yj)=0
D(Zn)=D(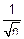
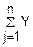 j)=
j)=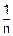
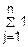 =
=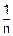 ·n=1
·n=1
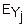 (u)=M(
(u)=M(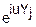 )=
)=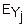 (0)+
(0)+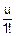
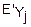 (u)+
(u)+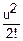
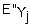 (u)+…=1+
(u)+…=1+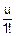 iM(Yj)-
iM(Yj)-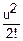 D(Yj)+…=1+0-
D(Yj)+…=1+0-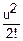 +…
+…
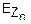 (u)=
(u)=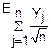 (u)=
(u)=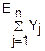 (
(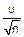 )=(
)=(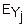 (
(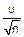 ))n=(1-
))n=(1-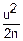 +o(
+o(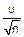 ))n
))n
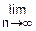
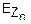 (u)=
(u)=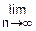 (1-
(1-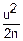 +o(
+o(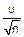 ))n=exp(-
))n=exp(-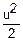 )
)
Интегральная теорема Муавра-Лапласа.
Проводится серия из n независимых испытаний Бернулли, в каждом из которых некоторое событие A появляется с одной и той же вероятностью p или не появляется с одной и той же вероятностью q=1-p.
Тогда pn(m1≤m≤m2)≈Φ(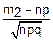 )-Φ(
)-Φ(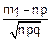 )
)
Φ(z)=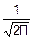
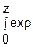 (-
(-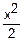 )dx
)dx
Свяжем с каждым испытанием случайную величину Xj. Эта величина принимает значение 1, если в испытании с номером j событие A произошло (вероятность этого p), и 0 в противном случае (вероятность этого
q=1-p).
Тогда имеется последовательность случайных величин X1, X2…Xn.
Величины X1, X2…Xn независимы, одинаково распределены, имеют конечные и одинаковые математические ожидания M(Xj)=p и конечные и одинаковые дисперсии D(Xj)=pq. Таким образом, величины X1, X2…Xn удовлетворяют условиям теоремы Ляпунова.
Сумма этих величин, при достаточно большом значении n имеет нормальный закон распределения, т. е. F(x)=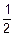 +Φ(
+Φ(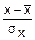 )
)
 =M(X)=np
=M(X)=np
σx=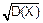 =
=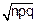
p(m1≤m=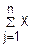 j≤m2)≈F(m2)-F(m1)=Φ(
j≤m2)≈F(m2)-F(m1)=Φ(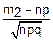 )-Φ(
)-Φ(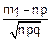 )
)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 419; Нарушение авторских прав?; Мы поможем в написании вашей работы!