В реверсивном счётчике объединяются схемы суммирующего и вычитающего счётчиков. Кроме того, предусматривается возможность управления направлением счёта

Характерной чертой асинхронного счётчика является то, что импульсы счёта поступают только на триггер младшего разряда. Счётный же вход каждого последующего триггера соединён с выходом предыдущего.

C T TT T TT T TT C CT2 1 Q1 графическое

2 Q₂ изображение
R R R R R 4 Q₃ имеет вид:

Выходы счётчика помечаются весовыми коэффициентами двоичных разрядов. Начальное состояние счётчика устанавливается сигналом по входу R.

Работа счётчика может быть описана с помощью временных диаграмм:
C
1 2 3 4 … 8 t Первый импульс установит младший
Q₁ триггер счётчика в состояние 1. Поскольку
0 1 0 1 0… 1 t фронт импульса тригггерами не восприни-
Q₂ нимается, то в результате счётчик перехо-
0 0 1 1 0… 1 t дит из начального состояния в первое: на
Q₃ выходе код единицы.

0 0 0 0 1 1 t Вторым импульсом младший триггер переключается в противоположное состояние, формируя на своём выходе срез импульса. В результате второй триггер перейдёт в состояние 1, а счётчик – во второе состояние: на выходе код числа 2.

Третий триггер установится в единичное состояние лишь четвёртым по счёту импульсом, когда младшие триггеры последовательно переключатся в нулевое состояние.

Далее младшие триггеры повторят цикл счёта с первого по третий импульсов. В результате после седьмого по счёту импульса все триггеры счётчика будут установлены в единичное состояние: на выходе счётчика код числа 7.

Восьмой импульс переведёт счётчик в начальное состояние, после чего он будет готов к счёту новой последовательности из восьми импульсов.

Таким образом, модуль счёта рассмотренного счётчика равен восьми.

Следует отметить, что при использовании триггеров, управляемых фронтом счётных импульсов, счётный вход каждого последующего триг-гера необходимо соединить с инверсным выходом предыдущего.

Работу рассмотренного счётчика можно также представить как процесс суммирования предыдущего его состояния с единицей. Тогда процесс переключения триггеров можно сопоставить с процессом распространения переноса при суммировании двоичных чисел. Т.е. считать, что каждый последующий триггер переключается сигналом переноса, формируемым на выходе предыдущего триггера.

Поскольку этот процесс протекает последовательно от триггера к триггеру, то подобные схемы счётчиков называются счётчиками с последовательным переносом.

Из временных диаграмм следует, что в наихудшем случае (например, переход в начальное состояние) новое состояние n-разрядного счётчика устанавливается с задержкой nt_П, где t_П – время переключения триггера. Следовательно, допустимая частота входных импульсов равна 1/nt_П.

Более высоким быстродействием обладают синхронные счётчики:

Q₁ Q₂ Q₃
Характерным для син-
& & хронных счётчиков явля-
ется то, что импульсы
ТТ V TT V TT счёта поступают на все
T триггеры одновременно.
T T Логические элементы
C И используются для формирования сигналов переноса.

Из схемы видно, что новый импульс счёта, изменяющий состояние старшего триггера, может поступить только после того, как сформируется разрешающий сигнал сначала на выходе первого элемента И, затем второго и т.д.

Следовательно, перенос остался последовательным.

Время установки состояния такого счётчика при n разрядах определяется выражением: t_П + (n – 1)t_И, где t_И – время задержки переключения логического элемента И.

Поскольку t_И<t_П, то быстродействие синхронного счётчика с последовательным переносом существенно выше, чем асинхронного.

Для дальнейшего увеличения быстродействия организуется параллельный перенос:

Q₁ Q₂ Q₃ В этом случае задержка

установки состояния счёт-

чика определяется суммой

& & t_П + t_И и не зависит от чис-

ла его разрядов.
ТТ V TT V TT
T Однако при этом необ-
T T ходимо использовать эле-
C менты И с нарастающим от разряда к разряду числом входом.

В результате нарушается регулярность (однотипность), структуры счётчика, что снижает технологичность изготовления много разрядных счётчиков в виде интегральных микросхем.

Поэтому при построении много разрядных счётчиков используются схемы с параллельно-последовательным переносом:

Вх. С СТ2 1 С СТ2 1 В этой схеме счётчики небольшой раз-

2 2 рядности с параллельным переносом сое-

4 4 динены между собой последовательно.

Сбр. R 8 R 8 Задержка установки состояния такого

многоразрядного счётчика пропорцио-нальна числу составляющих его счётчиков.

Вычитающие двоичные счётчики имеют следующие свойства:

- начальным является единичное состояние;

- очередное число в последовательности чисел, формируемой счётчиком, получается вычитанием 1 из предыдущего.

Таким образом, если считать, что суммирующий счётчик формирует числовую последовательность в прямом коде, то вычитающий счётчик будет формировать ту же последовательность чисел, но в обратном коде.

Следовательно, схемы вычитающего счётчика отличаются от схем суммирующего счётчика лишь тем, что в качестве выходов используются инверсные выходы триггеров.

Кроме того, поскольку речь идёт о вычитании, сигнал переноса называется займом.

Реверсивные двоичные счётчики.

Многие реверсивные счётчики дополняются входами предварительной установки состояния.

Один из вариантов условного графического изображения таких счётчиков имеет вид:

D₁ CT2 1 Q₁ Подача импульсов счёта на вход +1 задаёт режим

D₂ 2 Q₂ суммирования, а на вход -1 – режим вычитания.

D₃ 4 Q₃ Сигналом по входу L счётчик устанавливается в

D₄ 8 Q₄ состояние, заданное на входах D. При этом безразлич-

L но, подаются счётные импульсы или нет.

+1 Сигналом по входу R счётчик устанавливается в

-1 ³15 нулевое состояние. При этом безразлично наличие или

R £0 отсутствие как счётныех импульсов, так и сигнала предварительной установки состояния счётчика.

Выходы разрядов счётчика помечаются весовыми коэффициентами двоич-ных разрядов.

На выходе переноса (помечен ³ 15) активный сигнал появляется при единичном состоянии счётчика, а на выходе займа (помечен £ 0) – при нулевом.

Выходы переноса и займа используются в основном для построения многоразрядного реверсивного счётчика. При этом выходы переноса и займа предыдущего счётчика соединяются, соответственно, с входами +1 и -1 последующего счётчика.

В интегральном исполнении выпускаются суммирующие и реверсивные счётчики. Как правило, микросхемы двоичных счётчиков имеют 4 разряда. В маркировке микросхем счётчиков используются буквы ИЕ, например, К155ИЕ5.

3.10. Счётчики с произвольным модулем счёта.

На практике бывает потребность в построении счётчиков по модулю, мень-шего максимального, т.е. < 2ⁿ. Такие счётчики строятся на основе двоичных счётчиков.

При использовании суммирующего

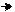
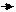
0 1 К_С-1 2ⁿ-1 счётчика последовательность чисел на
выходе счётчика по модулю К_С совпадает с двоичной от 0 до К_С-1, после чего следует начальное состояние и цикл счёта повторяется.

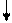
При использовании вычитающе-

2ⁿ-1 2ⁿ-2 2ⁿ-K_c+1 0 го счётчика выходная последова-тельность чисел совпадает с двоичной от 2ⁿ-1 до 2ⁿ-К_С+1.

Таким образом, в любом случае необходимо исключить "лишние" состо-яния счётчика путём замены на начальное в первом случае К_С-е состояние, а во втором случае – состояние 2ⁿ-К_С.

Отсюда напрашивается следующая схема построения счётчика по модулю К_С на основе суммирующего и вычитающего счётчика:

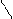
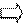
С СТ2 СО C CT2 СО В момент выявления

Q К_С z Q 2ⁿ-K_C z требуемого состояния

R S двоичного счётчика

схема обнаружения (СО) вырабатывает сигнал z его установки в начальное состояние.

Очевидно, что СО реализует функцию конституенты нуля или единицы относительно требуемого состояния счётчика.

При этом в общем случае (отсутствие нужных входов принудительной установки) необходимо учитывать все разряды соответствующего числа на выходе счётчика.

ЛЕКЦИЯ 12

Например, требуется построить счётчик по модулю 10 на основе суммирующего счётчика. Активным сигналом по его R-входу является 1.

Для решения задачи необходим ù log₂10 é= 4-разрядный счётчик. При этом СО должна реализовывать ФАЛ: z = .

Однако при наличии нужных входов принудительной установки для выявления требуемого состояния счётчика достаточно учитывать только единичные или только нулевые позиции соответствующего двоичного числа.

Основанием для этого является следующее свойство двоичных чисел: каждое последующее число отличается от всех предыдущих расположением единиц или, что то же самое, нулей.

Так, при использовании суммирующего счётчика с входом R достаточно учитывать только единичные позиции числа К_С. В противном случае счётчик никогда не выйдет из начального, нулевого, состояния.

Тогда ФАЛ, описывающая СО последнего примера, примет вид: z = x₃x₁.

Дата добавления: 2014-01-07