
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Синтез информационного обеспечения АС модульного типа
|
|
|
|
Синтез технической структуры АСУТП на основе конденсации графовой функциональной модели системы
В.Я. Войтенко, А.В. Кузнецов «Приборы и системы управления», №4, 1991г.
Рассмотрим синтез оптимальной по числу технических элементов структуры АСУТП для одного ее уровня, например, нижнего (локального) уровня иерархии АСУТП, с дальнейшим обобщением и применением полученных результатов для синтеза ее последующих уровней. Будем считать, что рассматривается структура технических средств АСУТП, включающая в качестве элементов технические устройства (например, контроллеры) и линии управления, контроля и сигнализации в качестве линий связи.
Постановка задачи и ее математическая модель
Техническую структуру локального уровня АСУТП, на которую возлагается решение некоторого множества L предназначенных для автоматизированного выполнения задач (функций), определим отображением d множества L={ℓj}, j=1,..,k на множество M={mi}, i=1,..,n технических документов (процессоров) АСУ, которые необходимо использовать для построения технической структуры (ТС) локального уровня АСУТП, т.е.
d: L → M → {ℓj} → {mi} (1)
при условии экстремума некоторого критерия оптимальности Qопт ТС АСУТП, характеризующего степень рациональности выбора числа n технических элементов АСУТП с учетом связности задач системы и удовлетворения следующих ограничений:
1. однородность элементов ТС АСУТП и равнозначности связей между задачами одного уровня;
2. согласованности величин информационной емкости Ij задач ℓj локального уровня управления с допустимыми объемами памяти Vj* устройств ЭВТ, реализующих технические элементы АСУТП; при этом из-за предыдущего ограничения справедливо равенство V1*=V2*=…=Vn*=V*;
3. не превышения времени tj решения (обработки) задач ℓj некоторых пороговых (допустимых) значений Ti*, определяемых динамикой технологического процесса (ТП);
4. замкнутости (разомкнутости) межэлементного шинного интерфейса ТС АСУТП одного уровня.
С учетом сделанных ограничений синтез оптимальной ТС АСУТП сводится к определению требуемого оптимального числа n однородных технических элементов АСУТП, необходимых для решения задач локального уровня АСУТП, и распределению связей между этими элементами. Другими словами, нужно определить минимальное число, а также состав и взаимосвязи подмножеств сильно связанных задач, каждое из которых решается своим техническим элементом mi; при этом число задач, входящих в состав таких подмножеств, может принимать значения от 1 (тогда число подмножеств равно k) до k (число подмножеств равно 1), а значит, и число n требуемых для их решения технических элементов согласно выражению (1) может варьироваться от k до 1.
Сильно связными будем полагать взаимно связные, а слабо связными – односторонне связные задачи рассматриваемого уровня иерархии ТС АСУТП.
Формализацию поставленной задачи проведем на базе математического аппарата теории графов.
В этом случае она может быть сформулирована следующим образом:
найти минимальное значение величины n, равное минимальному числу сильно связных компонент графа Gi; i=1,..n, информационного графа G:
G=(‹L, V, T›, ‹F, W›), где
L={ℓj}, j=1,..,k – множество автоматизируемых задач АСУТП локального уровня, соответствующих вершинам графа G;
V={vj}, j=1,..,k – множество, каждый элемент которого определяет требуемый в процессе решения j-й задачи объем памяти, непосредственно зависящий от значения информационной емкости Ij задачи ℓj, т.е. vj=f(Ij);
T={tj}, j=1,..k – множество, каждый элемент которого определяет время, требуемое для решения j-й задачи;
F={fjs}, j=1,..,k; s=1,..,k – множество связей (дуг графа G) между задачами, причем равенство индексов j=s допустимо, что соответствует связи каждой вершины графа G с самой собой посредством дуги, называемой петлей, изображение которой на графе, как правило, опускается с целью упростить его схему;
W={wjs}, j=1,..k; s=1,..,k – множество весов соответствующих дуг графа G, соединяющих его вершины; вследствие ограничения, сформулированного в п. 1) каждый элемент wjs множества W положим равным 1 (wjs=1),
причем таких сильных компонент, что
 : Gi≠0, Gi∩Gu=0, i,u=1,..,n; u≠i
: Gi≠0, Gi∩Gu=0, i,u=1,..,n; u≠i  =G
=G
и обеспечивается условие:
Qопт → max
при ограничениях
 (объем памяти процессора) (2)
(объем памяти процессора) (2)
 (время решения всех задач i-ым процессором) (3)
(время решения всех задач i-ым процессором) (3)
Рассмотрим на примере решение сформулированной задачи определения минимального числа, а также состава и взаимосвязей подмножеств сильно связных задач управления, контроля и сигнализации локального уровня АСУТП, каждое из которых будет решаться своим техническим элементом mi.
Пусть в результате функционального анализа объекта управления (ТП) установлено множество L={ℓj}, j=1,..,k задач, решение которых подлежит автоматизации. Описаны также все условные и безусловные, непосредственные и косвенные, прямые, обратные и взаимные, а также другие связи между ними, на основе чего выстраивается информационный граф G, вершинами которого являются сами задачи ℓj и их атрибуты (vj, tj), а ориентированными дугами – связи fjs между задачами. На рис. 3.15 дан пример такого графа G.
 |
Рис. 3.15. Информационный граф G задач локального уровня АСУТП
Алгоритм решения задачи
Поставленная задача решается на основе реализации процедуры конденсации G* графа G путем отыскания его сильных компонент, число которых априорно неизвестно.
Граф G* называемый конденсацией графа G, определяется следующим образом: каждая его вершина mi соответствует множеству вершин некоторой сильной компоненты Gi графа G, т.е. mi~Gi= (разным сильным компонентам из графа G отвечают разные вершины в конденсации G*); дуга fiu* существует в конденсации G* тогда, когда в графе G имеется такая дуга fjs, что вершина ℓj принадлежит сильной компоненте графа Gi, соответствующей вершине mi в конденсации G*, а вершина ℓs – сильной компоненте графа Gu, отвечающей вершине mu в конденсации G*, т.е.
(разным сильным компонентам из графа G отвечают разные вершины в конденсации G*); дуга fiu* существует в конденсации G* тогда, когда в графе G имеется такая дуга fjs, что вершина ℓj принадлежит сильной компоненте графа Gi, соответствующей вершине mi в конденсации G*, а вершина ℓs – сильной компоненте графа Gu, отвечающей вершине mu в конденсации G*, т.е.
 ~
~ ~
~
Сильными компонентами графа Gi будем считать максимальные подграфы графа G, обладающие заданным свойством. Поскольку в данном случае в качестве такого свойства выступает сильная связность вершин графа G, его сильные компоненты будут представлять собой подмножества (порожденные подграфы) взаимно связных вершин.
Требуется найти его сильные компоненты и построить конденсацию G*.
Эта процедура реализуется при использовании матриц достижимости RG и контрдостижимости QG графа G.
Матрица достижимости RG=||rjs|| определяется следующим образом:
 1, если вершина ℓs достижима из вершины ℓj (т.е. ℓj→ℓs)
1, если вершина ℓs достижима из вершины ℓj (т.е. ℓj→ℓs)
rjs=
0, в противном случае, т.е. ℓj → ℓs.
Вершина ℓs считается достижимой из вершины ℓj, если существует путь от вершины ℓj к вершине ℓs.
Все диагональные элементы матрицы RG равны 1, т.к. каждая вершина достижима из самой себя путем длиной 0. В качестве алгоритма построения матрицы достижимости RG можно предложить следующий:
Вход: Матрица AG смежности графа G, состоящая из строк A1, A2,…, Aj,…, Ak; Aj=(aj1,…, ajs,…, ajk)
Выход: Матрица достижимости RG, состоящая из строк R1, R2,..., Rj,…, Rk, где Rj=(rj1,…, rjs,…, rjk)
Алгоритм запишем в виде, использующем псевдоалгол:
Начало
1. для j от 1 до k шаг 1 цикл А
2. сформировать множество S индексов s таких, что ajs=1;
3. Rj:= Aj ; k:=0;
4. пока S≠0 цикл В
5. выбрать sєS;
6. Rj:=Rj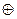 As;
As;
7. S:=S\{s};
8. K:=K {s};
{s};
9. Сформировать множество Ss индексов r таких, что asr=1;
10. S:=S (Ss\K);
(Ss\K);
11. конец цикла В;
12. возврат Rj;
13. конец цикла А;
Конец
Для примера матрица смежности AG имеет вид:
| ℓ1 | ℓ2 | ℓ3 | ℓ4 | ℓ5 | ℓ6 | ||
| ℓ1 | |||||||
| ℓ2 | |||||||
| AG= ℓ3 | |||||||
| ℓ4 | |||||||
| ℓ5 | |||||||
| ℓ6 | |||||||
Применяя описанный выше алгоритм, получаем следующую матрицу достижимости RG:
| ℓ1 | ℓ2 | ℓ3 | ℓ4 | ℓ5 | ℓ6 | ||
| ℓ1 | |||||||
| ℓ2 | |||||||
| RG= ℓ3 | |||||||
| ℓ4 | |||||||
| ℓ5 | |||||||
| ℓ6 | |||||||
Матрица контрдостижимости QG=║qjs║ определяется следующим образом:
 1, если из вершины ℓs графа G достижима вершина ℓj (т.е. ℓj←ℓs)
1, если из вершины ℓs графа G достижима вершина ℓj (т.е. ℓj←ℓs)
qjs=
0, в противном случае, т.е. ℓj ← ℓs.
При этом qjs=1, если j=s.
Очевидно, что матрица QG есть транспонированная матрица RG.
Для нашего примера имеем:
| ℓ1 | ℓ2 | ℓ3 | ℓ4 | ℓ5 | ℓ6 | ||
| ℓ1 | |||||||
| ℓ2 | |||||||
| QG= ℓ3 | |||||||
| ℓ4 | |||||||
| ℓ5 | |||||||
| ℓ6 | |||||||
На следующем этапе алгоритма выполняется поэлементарное умножение матриц RG и QG графа G, в результате чего получаем RG 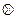 QG:
QG:
| ℓ1 | ℓ2 | ℓ3 | ℓ4 | ℓ5 | ℓ6 | ||
| ℓ1 | |||||||
| ℓ2 | |||||||
RG 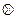 QG= ℓ3 QG= ℓ3
| |||||||
| ℓ4 | |||||||
| ℓ5 | |||||||
| ℓ6 | |||||||
При этом строка ℓj матрицы RG 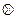 QG содержит единицы только в тех столбцах ℓs, для которых выполняется условие: вершины ℓj и ℓs взаимно достижимы. В других местах строки стоят нули. Таким образом, две вершины графа G находятся в одной и той же сильной компоненте тогда, когда соответствующие им строки (или столбцы) в матрице RG
QG содержит единицы только в тех столбцах ℓs, для которых выполняется условие: вершины ℓj и ℓs взаимно достижимы. В других местах строки стоят нули. Таким образом, две вершины графа G находятся в одной и той же сильной компоненте тогда, когда соответствующие им строки (или столбцы) в матрице RG 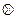 QG идентичны.
QG идентичны.
Следующий шаг алгоритма – преобразование матрицы RG 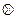 QG путем транспонирования ее строк и столбцов в блочно-диагональную матрицу (RG
QG путем транспонирования ее строк и столбцов в блочно-диагональную матрицу (RG 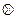 QG)′, каждая из диагональных подматриц (блоков) которой соответствует сильной компоненте графа G и содержит только единичные элементы, поскольку вершины, которым отвечают строки, имеющие единицу в столбце ℓs, образуют множество вершин сильной компоненты, содержащей вершину ℓs. Все остальные блоки данной матрицы имеют нули. Для нашего примера имеем:
QG)′, каждая из диагональных подматриц (блоков) которой соответствует сильной компоненте графа G и содержит только единичные элементы, поскольку вершины, которым отвечают строки, имеющие единицу в столбце ℓs, образуют множество вершин сильной компоненты, содержащей вершину ℓs. Все остальные блоки данной матрицы имеют нули. Для нашего примера имеем:
| ℓ1 | ℓ5 | ℓ2 | ℓ3 | ℓ4 | ℓ6 | ||
| ℓ1 | |||||||
| ℓ5 | |||||||
(RG 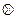 QG)′= ℓ2 QG)′= ℓ2
| |||||||
| ℓ3 | |||||||
| ℓ4 | |||||||
| ℓ6 | |||||||
Анализ матрицы (RG 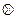 QG)′ позволяет получить число n и состав подмножеств сильно связных задач локального уровня АСУТП, решаемых каждое своим mi-м техническим элементом i=1,..,n. В данном примере в состав G входит три сильные компоненты, следовательно, число однородных технических элементов, которые могут быть использованы для построения оптимальной ТС локального уровня АСУТП, равно 3, т.е. имеем:
QG)′ позволяет получить число n и состав подмножеств сильно связных задач локального уровня АСУТП, решаемых каждое своим mi-м техническим элементом i=1,..,n. В данном примере в состав G входит три сильные компоненты, следовательно, число однородных технических элементов, которые могут быть использованы для построения оптимальной ТС локального уровня АСУТП, равно 3, т.е. имеем:

|

|

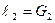 ~
~
 ~
~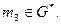
На основе блочно-диагональной матрицы (RG 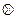 QG)′, а также структуры самого информационного графа G (см. рис. 3.12) строится его конденсация – граф G*, определяющий связи между mi-ми техническими элементами ТС АСУТП на локальном уровне, i=1,2,3 (см. рис. 3.16).
QG)′, а также структуры самого информационного графа G (см. рис. 3.12) строится его конденсация – граф G*, определяющий связи между mi-ми техническими элементами ТС АСУТП на локальном уровне, i=1,2,3 (см. рис. 3.16).
 |
Рис. 3.16. Конденсация G* графа G
В соответствии с определением конденсации графа и его сильных компонент, а также с учетом принятых ограничений (2) и (8) для элементов графа G* справедливы соотношения:

где i=1,2,3 для рассмотренного примера.
Кроме того, имеют место соответствия:
f21*~f21; f23*~f24; f31*~f31
Таким образом, для построения оптимальной по числу элементов n ТС АСУТП определены все ее составные части: число n технических элементов, состав подмножеств сильно связных задач, решаемых каждым из них, а также взаимосвязи между элементами ТС локального уровня АСУТП.
Если в ограничении, сформулированном в п. 4, задана замкнутость межэлементного шинного интерфейса данного уровня ТС АСУТП, то на основании результатов анализа блочно-диагональной матрицы (RG  QG)′, а также полученных в конденсации G* (см. рис. 2) связей fiu* (ориентированных дугах графа G*)
QG)′, а также полученных в конденсации G* (см. рис. 2) связей fiu* (ориентированных дугах графа G*)
Выстраивается искомая децентрализованная ТС АСУТП в целом с единственным (локальным, первым, нижним) уровнем иерархии (см. рис. 3.17).
 |
Рис. 3.17. Децентрализованная одноуровневая оптимальная ТС АСУТП
В случае, когда в ограничении на ТС АСУТП определена разомкнутость соответствующего интерфейса или требуется построение многоуровневой иерархической ТС АСУТП, с учетом связей fiu* составляется информационный граф G(2) задач второго уровня ТС, выстраиваемый по результатам функционального анализа множества задач (функций) этого уровня, лежащих в плоскости среза локального уровня, но решаемых соответственно на втором уровне иерархии ТС АСУТП. После этого относительно данного уровня ТС повторяется вся ранее описанная процедура синтеза. Аналогично выстраивается и все последующие уровни иерархической АСУТП.
Физический эффект оптимизации обусловлен, во-первых, сокращением числа связей между задачами каждого уровня ТС (на основе их внутреннего представления в соответствующих технических элементах), требующих взаимодействия различных элементов одного уровня, что увеличивает оперативность обмена информацией при соблюдении ограничений, определяемых выражениями (2) и (3), и, во-вторых, распараллеливанием решения только слабо связных задач фиксированного уровня ТС АСУТП; при этом сильно связные задачи, образующие свою сильную компоненту в информационном графе задач соответствующего уровня, предлагается решать последовательно на одном своем техническом элементе, т.е. задачи разных сильных компонент решаются параллельно, а в составе одной сильной компоненты – последовательно.
При этом следует иметь в виду следующее:
- Если каждая задача решается своим техническим элементом, то это дает возможность параллельной обработки всех задач одного уровня ТС, что приводит к увеличению оперативности обработки. Однако при этом возможна задержка при организации обмена между элементами, т.е. имеют место их простаивания в ожидании исходной информации. Кроме того, усложняются протоколы обмена, системные алгоритмы, модели и программы управления системой, заметно поднимается и стоимость такой системы.
- Если все задачи решаются одним элементом (одномашинная или однопроцессорная вычислительная система), то здесь имеется возможность внутреннего представления всех связей между задачами, что устраняет задержки обмена и простаивания технических элементов, ожидающих в качестве исходных данных для решения своей задачи, результатов решения других задач на других элементах. Однако здесь возможно появление задержки из-за образующихся очередей задач на обслуживание, т.к. нет возможности для их параллельной обработки.
Приведенные доводы свидетельствуют в пользу предлагаемого метода синтеза оптимальной ТС АСУТП, свободного от перечисленных недостатков.
Лекция 15
3.8. Обобщенная математическая модель определения рациональной структуры распределенной АСУ
При разработке автоматизированных систем управления возникает необходимость определения рациональной структуры системы, распределения функций, реализуемых системой, между ее узлами или уровнями. Функции, возлагаемые на технические средства АСУ, зависят от наличия соответствующих математических моделей и методов их решения, а также от возможности их реализации комплексом технических средств АСУ. В свою очередь КТС выбирается для определенного круга решаемых задач с учетом ограничений на ресурсы при его создании, а также с учетом того, что выбранные задачи должны, достаточно эффективно, выполнятся комплексом технических средств.
Под определением структуры АСУ будем понимать следующие операции:
1. Выбор задач управления, возлагаемых на технические средства АСУ.
2. Выбор алгоритмов их реализации в АСУ.
3. Распределение выбранных задач по узлам (уровням) системы.
4. Определение КТС в узлах АСУ.
Выбранная структура считается рациональной, если общая эффективность разрабатываемой АСУ максимальна.
Для формализации задачи введем ряд обозначений.
Пусть Е – это множество задач управления. Каждой задаче припишем номер (индекс) i=1,..,I. Обозначим через Mi множество алгоритмов решения i-ой задачи в АСУ, включая решение задачи без применения технических средств, Mi={k/k=1,..,ki}.
Через ║ ║ обозначим матрицу связи между задачами. Задачи i и i′ считаются связанными, если для решения i′-й задачи используется информация, являющаяся входной для i-й задачи, при этом
║ обозначим матрицу связи между задачами. Задачи i и i′ считаются связанными, если для решения i′-й задачи используется информация, являющаяся входной для i-й задачи, при этом  имеет смысл среднего потока информации от i-й задачи к i′-й. Если задачи не связаны, то
имеет смысл среднего потока информации от i-й задачи к i′-й. Если задачи не связаны, то  =0.
=0.
Пусть Q – множество номеров узлов (уровней) АСУ, причем Q={j/j=1,..,J}; ║ ║ - матрица удельных затрат на передачу информации из j-го узла в j′ (для не связных узлов
║ - матрица удельных затрат на передачу информации из j-го узла в j′ (для не связных узлов  =∞, а
=∞, а  =0).
=0).
Обозначим через F множество номеров технических средств, т.е. F={ℓ/ℓ=1,..,L}, mℓ - величина, характеризующая ресурсы ℓ-го технического средства. Кроме того, аikj – эффективность решения i-й задачи k-м способом в j-м узле, mik – потребность в ресурсах технических средств i-й задачи, решаемой k-м способом (например, в машинном времени, памяти и т.п.); Cℓj – затраты на эксплуатацию ℓ-го технического средства в j-м узле, Kℓ - капитальные затраты на технические средства, Kik – затраты на разработку и внедрение i-й задачи в k-м варианте.
Напомню, что под термином «задача» понимается комплекс взаимосвязанных операций по обработке информации и принятию решений. Выбор этих задач может осуществляться, например, экспертным методом, о чем уже говорилось ранее. Также экспертным методом может быть определена эффективность решения задач аikj и другие необходимые для анализа данные.
Таким образом, задача состоит в максимизации эффекта от разрабатываемой структуры АСУ, который определяется эффективностью решения задач управления в соответствующих узлах системы, т.е. зависит от выбора уровня и алгоритма решения задач управления с учетом затрат на обмен информацией между задачами, решаемыми на различных уровнях, и затрат на эксплуатацию системы.
Введем следующие переменные:
 1, если i-я задача решается в j-м узле k-м способом
1, если i-я задача решается в j-м узле k-м способом
xikj=
0 в противном случае
 |
1, если j-й узел оборудуется ℓ-м техническим средством
xℓj=
0 в противном случае.
Задача может быть теперь записана в следующем виде:

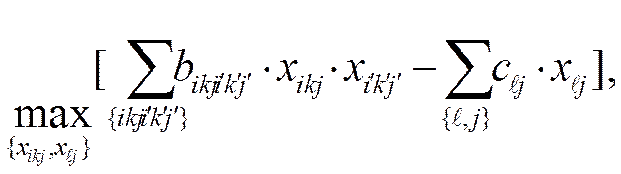 (1)
(1)
аikj, если ikj=i′k′j′
где bikji′k′j′= (2)
-αikji′k′j′*γjj′, если ikj≠i′k′j′.
Величина bikji′k′j′ равна эффективности решения k-го варианта i-й задачи в j-м узле, т.е. аikj, если ikj=i′k′j′ и равна затратам на передачу информации из j-го узла в j′-й в противном случае.
В качестве ограничений здесь выступают следующие:
(3)  , т.е. каждая задача должна быть решена, причем только в одном каком-либо узле и только одним каким-либо способом;
, т.е. каждая задача должна быть решена, причем только в одном каком-либо узле и только одним каким-либо способом;
 (4)
(4) 
1, если j-й узел оборудуется ℓ-м техническим средством
xℓj=
0 в противном случае.
т.е. общие затраты на разработку АСУ, состоящие из стоимости на капитальные затраты на технические средства и на разработку и внедрение задач не должны превышать заданной величины K;
(5) 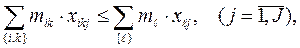
т.е. используемые технические средства имеют определенные ресурсные ограничения.
Рассмотренная задача является нелинейной задачей математического программирования.
Если заранее произведен выбор технических средств и известно, что задачи независимы, то выражение (1) примет вид:
(6)  при ограничениях:
при ограничениях:
(7) 
(8) 
(9) 
Задачу (6) - (9) можно свести к двухиндексной, если ввести переменную xfj. Взаимно однозначное соответствие между множествами индексов {f} и {ik} устанавливается следующим соотношением:
f=k+bi, 
В этом случае задача будет иметь вид:
 (10)
(10)
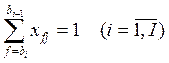 (11)
(11)
 (12)
(12)
 (13)
(13)
Если задачи зависимы, то вместо (10) следует записать
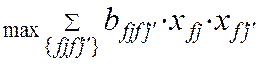 (14)
(14)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 340; Нарушение авторских прав?; Мы поможем в написании вашей работы!