
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разрабатываемых на проектных стадиях создания АС
|
|
|
|
Задача определения оптимальной величины блока данных
Задача и модель определения числа и состава информационных массивов
Пусть в результате диагностического анализа проектируемой АС для заданного комплекса задач управления определено множество программных модулей M={m1, m2,…, mv,…, mV}, где V – число таких модулей. Для каждого модуля mv установлена средняя частота его функционирования Qv (v=1,..,V) в заданный интервал времени, например, в сутки. Известно также множество информационных элементов D={d1, d2,…, dℓ,…, dL}, где L – число таких элементов, с которыми связаны модули множества M. Каждый информационный элемент dℓ характеризуется длиной записи, например, в байтах λℓ. Величины λℓ (ℓ=1,..,L) образуют вектор Λ={λ1, λ2,…, λℓ,…, λL}.
Для каждого модуля mv (v=1,..,V) информационный элемент dℓ (ℓ=1,..,L) может быть входом, выходом или модуль mv никак не связан с информационным элементом dℓ. В первом случае будем говорить, что модуль mv считывает элемент dℓ, а во втором – модуль mv записывает элемент dℓ.
Связь между модулями и информационными элементами может быть задана в виде двух матриц. Bс=║bvℓc║ и Bз=║ bvℓз ║, где bvℓc(bvℓз) равен единице, если ℓ-й информационный элемент (ℓ=1,..,L) считывается (записывается) v-м модулем (v=1,..,V) и равен нулю в противном случае.
Обозначим через F возможное число информационных массивов, по которым распределяются информационные элементы. Очевидно, что F≤L.
Введем следующие булевы переменные:
 1, если ℓ-й информационный элемент размещен в f-й массив
1, если ℓ-й информационный элемент размещен в f-й массив
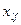 f=
f=
 0, в противном случае.
0, в противном случае.
1, если 
zvfс= (1)
0, если 
 1, если
1, если 
zvfз= (2)
0, если 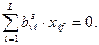
Другими словами zℓfс(з) принимает значение 1, если модуль mv связан с информационным элементом dℓ, который находится в массиве f.
Переменные xℓf (ℓ=1,..,L; f=1,..,F) образуют матрицу X=║ xℓf ║, определяющую распределение информационных элементов по информационным массивам. Матрицы Zc=║ zℓfс ║ и Zз=║ zℓfз ║ размерности V*F каждая определяют связь программных модулей с информационными массивами.
Сформулированную задачу определения числа и состава информационных массивов можно теперь формально представить в виде следующей модели:
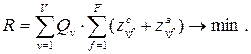 (3)
(3)
при ограничениях
 (4)
(4)
 (5)
(5)
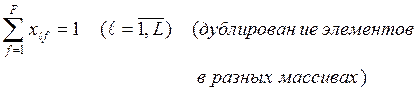 (6)
(6)
где zℓfс и zℓfз определяются выражениями (1) и (2);
Nf – ограничения на общее число информационных элементов в f-м массиве;
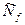 - ограничения на длину записи в f-м массиве.
- ограничения на длину записи в f-м массиве.
Значения величин 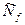 , Nf, f=1,..,F определяются разработчиком АСУ исходя из ограничений, наложенных на внешние запоминающие устройства выбранной ЭВМ.
, Nf, f=1,..,F определяются разработчиком АСУ исходя из ограничений, наложенных на внешние запоминающие устройства выбранной ЭВМ.
Задача (1) – (6) относится к классу задач целочисленного нелинейного программирования и может быть решена методом ветвей и границ. Алгоритм решения этой задачи будет рассмотрен в следующем семестре.
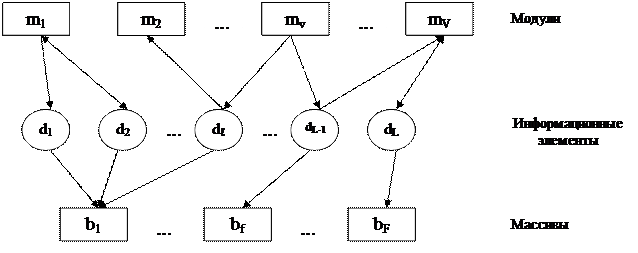
Данной задаче можно придать графовую интерпретацию: необходимо синтезировать двудольный граф 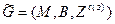 , имеющий минимальное число дуг при ограничениях на размеры и сложность информационных массивов, возможности дублирования и распределения информационных элементов по массивам, где:
, имеющий минимальное число дуг при ограничениях на размеры и сложность информационных массивов, возможности дублирования и распределения информационных элементов по массивам, где:
M – множество модулей: M={mv; v=1,..,V};
B – множество определяемых информационных массивов: B={bf; f=1,..,F};
Zс(з) – множество дуг, связывающих множество модулей с множеством массивов: Zс(з)=║zvfс(з)║.
 | |||
 |
Рис. 3.19. Графовая модель задачи
Рассмотрим следующий пример. Пусть после исследования проектируемой АСУ было выяснено, что необходимы 3 модуля, связанные с 6 информационными элементами. Эта связь и частота использования модулей в процессе функционирования АСУ приведены в таблице 1.
Таблица 1
| Номер модуля | Информационные элементы, считываемые модулями из БД | Информационные элементы, записываемые модулями в БД | Средняя частота использования модуля в единицу времени |
| 2, 3, 4, 5 | 1, 4 | ||
| 1, 2, 6 | |||
| 4, 5, 6 |
Длины соответствующих информационных элементов в килобайтах приведены в таблице 2.
Таблица 2
| Информационный элемент | ||||||
| Длина элемента, (КБ) |
Представим исходные данные в виде направленного двудольного графа 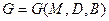 , где
, где 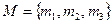 - множество модулей системы,
- множество модулей системы,  - множество информационных элементов,
- множество информационных элементов, 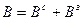 - матрица смежности графа, показывающая связи модулей с информационными элементами и имеющая следующий вид (см. табл. 1):
- матрица смежности графа, показывающая связи модулей с информационными элементами и имеющая следующий вид (см. табл. 1):
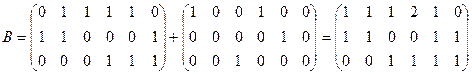 .
.
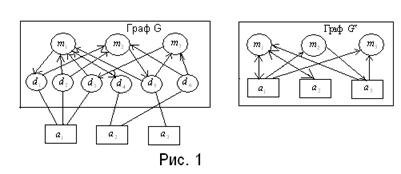
Граф 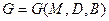 изображен на рис. 1, где
изображен на рис. 1, где 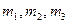 - модули;
- модули; 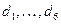 - информационные элементы;
- информационные элементы; 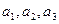 - массивы. Дуга направлена от модуля к элементу, если этот элемент записывается модулем, и от элемента к модулю, если элемент считывается модулем.
- массивы. Дуга направлена от модуля к элементу, если этот элемент записывается модулем, и от элемента к модулю, если элемент считывается модулем.
Один из вариантов построения двудольного графа  изображен на рис. 2. Он получен при условии, что информационные элементы
изображен на рис. 2. Он получен при условии, что информационные элементы 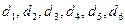 размещены в массивах
размещены в массивах 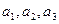 так, как показано на рис. 1.
так, как показано на рис. 1.
Среднее число обменов системы программных модулей с внешней памятью (базой данных) при размещении информационных элементов по массивам так, как показано на рис. 1, равно 100. Если, однако, в массив 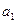 поместить элементы
поместить элементы  , в массив
, в массив  - элементы
- элементы 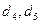 , а в массив
, а в массив 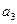 - элемент
- элемент  , то среднее число обменов сократится до 90. Таким образом, имеет место улучшение ранее составленного варианта размещения элементов по массивам.
, то среднее число обменов сократится до 90. Таким образом, имеет место улучшение ранее составленного варианта размещения элементов по массивам.
Рассматриваемая задача относится к классу задач нелинейного программирования с булевыми переменными.
Если число информационных элементов 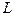 относительно невелико, то ее решение можно получить методом прямого перебора всех вариантов распределения информационных элементов по информационным массивам. Для этого строят дерево вариантов по следующей схеме: первый информационный элемент помещают в первый информационный массив; второй – в первый массив или во второй; третий – в первый, второй или третий массив и т.д.
относительно невелико, то ее решение можно получить методом прямого перебора всех вариантов распределения информационных элементов по информационным массивам. Для этого строят дерево вариантов по следующей схеме: первый информационный элемент помещают в первый информационный массив; второй – в первый массив или во второй; третий – в первый, второй или третий массив и т.д.
Очевидно, что число слоев такого дерева равно 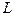 , а число вершин в
, а число вершин в 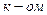 слое (
слое (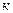 - номер информационного элемента) рано
- номер информационного элемента) рано 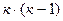 .
.
После построения 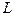 -го слоя дерева вариантов для каждого из них проверяются условия (4), (5) и (6) и среди им удовлетворяющих выбирается вариант с минимальным значением функционала (3).
-го слоя дерева вариантов для каждого из них проверяются условия (4), (5) и (6) и среди им удовлетворяющих выбирается вариант с минимальным значением функционала (3).
При большом числе информационных элементов 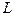 более рациональным является использование метода «ветвей и границ».
более рациональным является использование метода «ветвей и границ».
Точная нижняя оценка множества решений 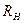 достигается в том случае, если все информационные элементы распределены в один информационный массив. Учитывая, что каждый считываемый или записываемый информационный элемент, по крайней мере, один раз должен быть использован хотя бы в одном программном модуле, то из выражения (3) непосредственно следует, что для вычисления
достигается в том случае, если все информационные элементы распределены в один информационный массив. Учитывая, что каждый считываемый или записываемый информационный элемент, по крайней мере, один раз должен быть использован хотя бы в одном программном модуле, то из выражения (3) непосредственно следует, что для вычисления 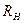 справедлива следующая формула:
справедлива следующая формула:
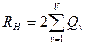 . (7)
. (7)
Точная верхняя граница (оценка) множества решений  достигается, если для каждого информационного элемента выделен свой информационный массив. В этом случае из выражения (3) непосредственно следует, что для вычисления
достигается, если для каждого информационного элемента выделен свой информационный массив. В этом случае из выражения (3) непосредственно следует, что для вычисления  справедлива следующая формула:
справедлива следующая формула:

 . (8)
. (8)
Оценку  любого подмножества решений в
любого подмножества решений в  вершине дерева ветвления можно определить по формуле:
вершине дерева ветвления можно определить по формуле:
 , (9)
, (9)
где 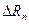 - приращение оценки в
- приращение оценки в  вершине дерева ветвления.
вершине дерева ветвления.
Величина оценки  любого подмножества решений в
любого подмножества решений в 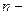 й вершине ветвления зависит от множества значений
й вершине ветвления зависит от множества значений 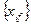 переменных, зафиксированных в этой
переменных, зафиксированных в этой 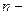 й вершине в процессе ветвления, и может быть вычислена по следующей формуле:
й вершине в процессе ветвления, и может быть вычислена по следующей формуле:
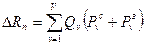 . (10)
. (10)
Величины 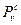 и
и 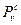 в выражении (10) определяются по следующим формулам:
в выражении (10) определяются по следующим формулам:
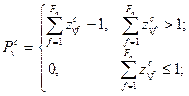 (11)
(11)
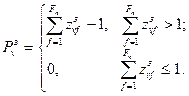 (12)
(12)
В выражениях (11) и (12) величина 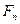 - это число образуемых массивов в
- это число образуемых массивов в 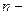 й вершине дерева ветвления, а
й вершине дерева ветвления, а 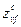 и
и  - булевы переменные, определяемые по формулам (1) и (2) соответственно при условии, что информационные элементы распределены по информационным массивам согласно
- булевы переменные, определяемые по формулам (1) и (2) соответственно при условии, что информационные элементы распределены по информационным массивам согласно 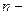 й вершине дерева ветвления.
й вершине дерева ветвления.
Алгоритм решения задачи определения числа и состава информационных массивов можно теперь представить в виде следующей последовательности шагов.
1. Вводят исходные данные задачи в виде массивов 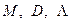 и матриц
и матриц  и
и 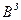 .
.
2. По формулам (7) и (8) вычисляют верхнюю и нижнюю границы  и
и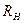 .
.
3. Распределяют информационный элемент 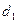 в информационный массив
в информационный массив 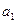 (строят первый слой дерева вариантов).
(строят первый слой дерева вариантов).
4. Полагая 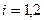 , помещают элемент
, помещают элемент  последовательно в информационный массив с номером
последовательно в информационный массив с номером 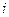 (строят второй слой дерева вариантов).
(строят второй слой дерева вариантов).
5. Для каждой вершины  го слоя (варианта распределения рассматриваемых информационных элементов по информационным массивам) последовательно проверяют выполнимость условий (4) и (6), полагая
го слоя (варианта распределения рассматриваемых информационных элементов по информационным массивам) последовательно проверяют выполнимость условий (4) и (6), полагая 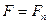 , где
, где 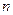 - номер рассматриваемой вершины. Для тех вершин, у которых условия (4) и (6) не выполняются, полагают
- номер рассматриваемой вершины. Для тех вершин, у которых условия (4) и (6) не выполняются, полагают 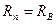 , для остальных вершин значения
, для остальных вершин значения  вычисляют по формулам (9) – (12).
вычисляют по формулам (9) – (12).
6. Находят вершину рассматриваемого  го слоя с номером
го слоя с номером  таким, что имеет место равенство
таким, что имеет место равенство  , где
, где  - множество номеров построенных вершин этого слоя.
- множество номеров построенных вершин этого слоя.
7. Проверяют, все ли слои дерева вариантов построены. Если да, то выполняют п. 9, в противном случае выполняют пункт 8.
8. Запоминают номер вершины  рассматриваемого
рассматриваемого  го слоя и строят вершины
го слоя и строят вершины 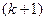 -го слоя, взяв в качестве исходной вершину с номером
-го слоя, взяв в качестве исходной вершину с номером  . После построения всех вершин
. После построения всех вершин 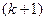 -го слоя переходят к п. 5.
-го слоя переходят к п. 5.
9. Находят решение задачи определения числа и состава информационных массивов, выбирая в каждом слое построенного дерева вариантов вершины с соответствующими номерами  .
.
Дерево вариантов применительно к рассмотренной выше задаче распределения 6 информационных элементов по информационным массивам приведены на рис. 2.

Точное решение этой задачи состоит в следующем: 1-й, 2-й и 3-й информационные элементы помещают в 1-й информационный массив; 4-й и 5-й информационные элементы помещают во 2-й информационный массив; 6-й информационный элемент составляет 3-й информационный массив. Общее время считывания, поиска и передачи требуемых данных при этом равно 90.
Лекция 17.
3.9.3. Задача выбора оптимальных методов организации полученных массивов и
размещения программных модулей и массивов во внешней памяти ЭВМ
Как об этом уже говорилось, критериями, используемыми для решения данных задач, являются: 1) минимизация суммарных затрат на создание, хранение и эксплуатацию информационных массивов и программных модулей СОД либо 2) минимизация общего времени обработки данных или времени решения одной из задач обработки данных.
Введем необходимые обозначения:
I={1, 2,…, i,…, I0} – множество задач обработки данных;
N=║niv║ - матрица принадлежности модуля к задаче, т.е.
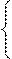 1, если модуль v используется для решения задачи i;
1, если модуль v используется для решения задачи i;
niv=
0 в противном случае.
Mс(з)=║mvfс(з)║ - матрица принадлежности массива к модулю,
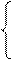 т.е.
т.е.
1, если f-й массив считывается (записывается) v-м модулем
mvfс(з)=
0 в противном случае.
Pi – частота решения i-й задачи в АСОИУ;
qvi – частота использования v-го модуля при решении i-й задачи;
Nf – количество информационных элементов в одной записи f-го массива;
Lf – число записей в f-ом массиве;
Rf=Nf*Lf – объем (размер) информационного массива f (общее число информационных элементов в массиве);
C0 – стоимость единицы рабочего времени процессора для решения вычислительных задач;
Cυ – приведенная стоимость единицы рабочего времени носителя информации υ-го типа с внешней памятью ЭВМ;
Sυ – стоимость блока управления υ-го типа носителя информации; υ=1,..,υ0
τvυ – время считывания v-го модуля, размещенного на υ-м типе носителя;
tfμυ(с), tfμυ(з) – время считывания (записи) f-го массива, организованного с использованием μ-го способа (можно использовать разные способы доступа к данным: прямой, произвольный по ключам и т.п., можно по-разному организовывать саму структуру данных: реляционная, иерархическая, сетевая и смешанная) и размещенного на υ-м типе носителя информации;
Tv – процессорное время реализации v-го модуля;
dυ – объем запоминающего устройства υ-го типа носителя информации;
av – размер v-го модуля;
Δτv – время работы процессора при поиске v-го модуля;
Δτfс (Δτfз) – время работы процессора при считывании (записи) f-го массива.
 Введем переменные:
Введем переменные:
1, если f-й массив организован μ-м методом и размещен на υ-м типе носителя информации
xfμυ=
0 в противном случае.
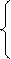 1, если v-й модуль размещен на υ-м типе носителя информации
1, если v-й модуль размещен на υ-м типе носителя информации
yvυ=
0 в противном случае.
1) Рассмотрим вначале постановку задачи выбора оптимальных методов организации информационных массивов, размещения массивов и модулей во внешней памяти, минимизирующих суммарные затраты на создание, хранение и эксплуатацию модульной АСОИУ.
Полные приведенные затраты C на решение задач АСОИУ являются суммой капитальных Ск и эксплуатационных затрат Сэ, т.е. С=Ск+Сэ.
Капитальные затраты Ск определяются выбором типа носителя информации, т.е. выбором технических средств и могут быть определены следующим выражением:
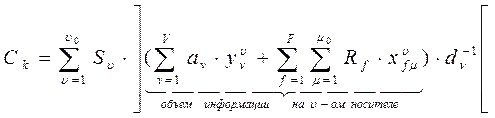 (1)
(1)
 - наименьшая целая часть, большая или равная α, где α – число носителей памяти типа υ=1,..,υ0.
- наименьшая целая часть, большая или равная α, где α – число носителей памяти типа υ=1,..,υ0.
Эксплуатационные затраты, в общем случае, содержат следующие составляющие:
- Стоимость непосредственной вычислительной работы процессора Сэобр; при решении задач i=1,..,I0;
- Стоимость процессорного времени при формировании адресов СэФА; для поиска нужных модулей и информационных элементов в соответствующих массивах;
- Стоимость записи и считывания массивов и модулей, т.е. стоимость обмена между оперативной и внешней памятью Сэобм. - важно только это слагаемое
Для вычисления этих составляющих могут быть использованы следующие формулы:
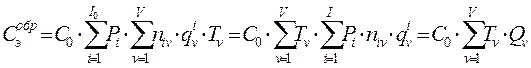 (2)
(2)
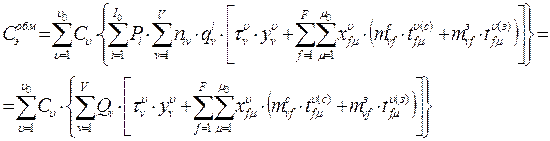 (3)
(3)
 (4)
(4)
Так как выражения (2) и (4) не содержат введенных переменных, то задача выбора способов организации и размещения модулей и массивов во внешней памяти формализуется следующим образом:
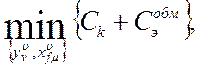 где Ск и Сэобм определяются формулами (1) и (3) при ограничениях:
где Ск и Сэобм определяются формулами (1) и (3) при ограничениях:
- на время Ti обмена с внешней памятью ЭВМ при решении i-й задачи:  (5)
(5)
- на используемый объем носителя информации υ-го типа:
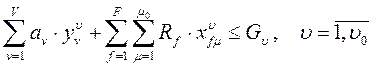 (6)
(6)
- на совместное размещение модулей и массивов в одном блоке носителя υ-го типа:
yvυ+xfμυ≤1 для заданных υ и (f, μ); (7)
- на размещение модулей на различных носителях:
 (8)
(8)
- на размещение массивов на различных носителях:
 (9)
(9)
- на размещение модулей и массивов на носителях определенного типа:
 для заданного υ (10)
для заданного υ (10)
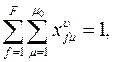 для заданного υ. (11)
для заданного υ. (11)
2) Рассмотрим постановку и решение задачи выбора оптимальных методов организации массивов и модулей во внешней памяти, минимизирующих: 1) общее время обработки данных; 2) время решения одной из задач управления.
В первом случае критерий имеет вид:
 (12)
(12)
Во втором – зафиксировав некоторое i:
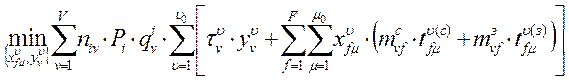 (13)
(13)
В этих задачах кроме ограничений (5) – (11) учитывается дополнительное ограничение на суммарные затраты П на создание и эксплуатацию АСУ:
Ск+Сэобм≤П (14), где Ск и Сэобм определяются формулами (1) и (3).
Сформулированные задачи являются задачами целочисленного линейного программирования с булевыми переменными.
В результате выше описанных этапов синтеза информационного обеспечения модульной АСУ получены следующие исходные данные, необходимые для определения оптимальной величины блока обмена данными с внешней памятью:
- система модулей программного обеспечения;
- множества информационных массивов и их связей с системой модулей;
- способы и характеристики размещения массивов и программных модулей на устройствах внешней памяти.
Введем необходимые переменные и обозначения:
Lfυ – число записей f-го массива, размещенного на υ-м типе запоминающего устройства;
M=║mvf║, v=1,..,V; f=1,..,F – матрица связи массивов с модулями системы:
 2, если f-й массив считывается и записывается v-м модулем,
2, если f-й массив считывается и записывается v-м модулем,
mvf= 1, если f-й массив только считывается v-м модулем,
0, если f-й массив не используется v-м модулем;
Xfυ – целочисленная переменная, определяющая число записей в блоке при считывании и записи в f-й массив, размещенный на υ-м типе запоминающего устройства;
Требуется выбрать множество переменных {xfυ} таким образом, чтобы минимизировать общее число обращений к внешней памяти с учетом технологических ограничений. Эта задача формулируется следующим образом:
 (15)
(15)
при ограничениях:
- на объем оперативной памяти Dv, доступной для данного v-го модуля:
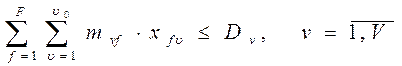 (16)
(16)
- на допустимый минимальный d υ и максимальный 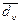 объема блока, размещенного в υ-м типе запоминающего устройства:
объема блока, размещенного в υ-м типе запоминающего устройства:
d υ ≤ xfυ ≤ 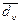 , f=1,..,F; υ=1,..,υ0 (17)
, f=1,..,F; υ=1,..,υ0 (17)
- на целочисленность величины блока:
xfυ ≥ 1, где xfυ – целое, f=1,..,F; υ=1,..,υ0 (18)
Данная задача является задачей дискретного программирования с нелинейной целевой функцией и линейными ограничениями и может быть решена алгоритмом, основанным на схеме «ветвей и границ».
Лекция 24
ГЛАВА 4. ТРЕБОВАНИЯ К СОДЕРЖАНИЮ ДОКУМЕНТОВ,
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!