Моделирование неравномерных случайных величин

Пусть распределение интервалов поступления через блок generate или advance не является равномерным или является равномерным с плавающими во времени значениями среднего и более допуска.

Для входа транзактов в модель необходимо использовать функции или СЧА. Использование функций, заданных в операндах блоков, зависит от контекста. В таблице приведены варианты использования функций и СЧА в качестве операндов А и В блоков generate и advance, т.е. следующие соотношения:

Операнд А	Операнд В	Результат
число или	СЧА	Генерируется случайное число на интервале +, равномерно распределенное
FN$DIS	отсутствует	Значение функции DIS (условное название некоторой дискретной функции)
отсутствует	FN$В	Данная комбинация недопустима
FN$DIS	число или СЧА	Сначала вычисляется значение функции DIS и берется целая часть этого значения (). Затем генерируется случайное число на интервале ±, равномерно распределенное
число или СЧА	FN$DIS	Сначала вычисляется значение функции DIS и берется целая часть этого значения (). После чего находится произведение ·. Результат равен целой части произведения.
FN$DIS 1	FN$DIS 2	Вычисляются значения функций DIS1 и DIS2 (пусть это будут числа и ), после чего находится ·и результат равен целой части произведения.

Пусть в моделируемой системе время обслуживания некоторым устройством равномерно распределено на интервале А±2, где среднее время обслуживания А с вероятностью 0,4 принимает значение 5, а с вероятностью 0,6 – значение 7. Эту ситуацию можно смоделировать следующим образом:

average t_t function RN1, D2

.4,5 / 1,7

Использует эту функцию в блоке advance:

advance fn$ average t_t, 2

Выполнение блока advance включает расчет функции average t_t. Это в свою очередь требует обращения к генератору случайных чисел RN1. если генератор выдаст число меньше, чем 0,4, то значение функции будет равно 5 и задержка транзакта составит 5 ± 2, равномерно распределенная.

В GPSS возможно задавать произвольные функции распределения случайных величин, используя табличную запись, поэтому можно задать только те функции, которые легко преобразовать для новых значений параметров.

К таким функциям относится: функция экспоненциального распределения с 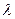=1, а также стандартное нормальное распределение с мат. ожиданием [M] = 0 и СКО = 1.

Эти ограничения не касаются в значительной мере языка GPSS World, в котором для задания различных функций распределения можно использовать библиотечные процедуры, написанные на языке PLUS.

Рассмотрим табличный способ задания пуассоновского потока заявок. Этот поток описывается так:

вероятность поступления k заявок в течение интервала времени t составляет:

k = 1, 2…; 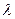- интенсивность потока.

Интервалы между соседними заявками распределены по экспоненциальному закону.

Согласно методу обратной функции, можно получить ряд чисел, которые имеют экспоненциальное распределение, если ряд случайных чисел r – равномерно распределен на интервале от 0 до 1.

Используем следующую формулу:

t_j = - T×ln (r_j), где

r_j – равномерно распределенное число;

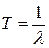- средний интервал времени поступления заявок, т.е. мат ожидание.

Определить экспоненциальное распределение с 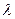= 1 можно следующим образом:

xp dis function rn 1, С24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/

.5,.69/.6,.915/.7, 1.2/.75, 1.38/

.8, 1.6/.84, 1.83/.88, 2.12/.9, 2.3/

.92, 2.52/.94, 2.81/.95, 2.99/.96, 3.2/

.97, 3.5/98, 3.9/.99, 4.6/.995, 5.3/

.998, 6.2/.999, 7/.9998, 8

Пуассоновский входящий поток с интенсивностью 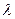, отличной от 1, моделируется с помощью блока generate следующим образом:

1. в качестве операнда А используется среднее значение интервала Т = 1/.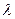

2. в качестве операнда В используется СЧА – значение функции XPDIS

Пример. Пусть среднее значение Т = 2 часа, а единица модельного времени 1 мин, тогда поступление заявок пуассоновского потока моделируется следующим образом: generate 120, fn$ XPDIS

Если необходимо моделировать задержку, распределенную по экспоненциальному закону со средним значением времени 345, то для этого используется блок advance 345, fn$ XPDIS.

Экспоненциальное распределение не всегда адекватно описывает время обслуживания и поступления требований в систему. Более реалистичным является распределение Эрланга. Это распределение получается с помощью последовательного соединения k устройств с экспоненциальным временем обслуживания. И соответственно это распределение будет называться распределением порядка k.

Пример. Поток Эрданга 2-го порядка со средним значением времени поступления 180 можно задать так:

generate,,, 1

sdfg advance 90, fn$ XPDIS

advance 90, fn$ XPDIS

split – разделение

split 1, sdfg

…

terminate 1

В нулевой момент времени в модель вводится транзакт, который в каждом из двух последующих блоков advance задерживается на экспоненциально распределенный промежуток времени.

Блок split создает одну копию транзакта и направляет ее на блок с меткой sdfg, а исходный транзакт поступает в модель.

generate 180

terminate 1

generate 4,1

start

Для того, чтобы исследовать свойства распределения Эрланга можно воспользоваться следующей моделью:

< описать функцию XPDIS >

TP table x₂, 1, 20, 50

generate,,, 1

sdfg advance 100, fn$ XPDIS

advance 100, fn$ XPDIS

advance 100, fn$ XPDIS

split 1, sdfg

savevalue 2, c 1

savevalue 2-, x 1

savevalue 1, c 1

tabulate TP

terminate 1

Запуск модели осуществляется командой start 100000000.

Для просмотра графика гистограммы необходимо запустить модель и после вывода стандартного отчета в пункте меню Windows выбрать пункт Windows table.

Дата добавления: 2014-01-07