Процессы массового обслуживания в экономических системах

Математические предпосылки создания имитационной модели

Команда GPSS World

Команды, необходимые для интерактивного взаимодействия и для построения программы. Они включают операторы описания данных, операторы управления и команды, используемые только в языке GPSS World.

Команда Start A, [B], [C], [D], где

А – задает значение счетчика завершения;

В – операнд выбора статистики, если его значение = NP, то вывод статистики блокируется.

Команда reset – вбрасывает 0 в статистику и СЧА системы, но не удаляет транзакты из модели. Значение относительно модели времени устанавливается в 0.

С1 – атрибут модельного времени. С1 = 0. А значение абсолютного модельного времени изменяется.

clear – сбрасывает всю накопленную статистику, удаляет все транзакты из модели. Относительное и абсолютное = 0.

Все изменяется, устройства не заняты и доступны.

<meta> equ А - Вычисляется выражение, заданное операндом А и присваивается переменной, время которой стоит в метке, его мы уже ранее применяли.

Системы массового обслуживания (СМО) широко распространены в повседневной жизни: ожидание в очереди при обслуживании в магазине, на заправке, в банке и т.д. Аналогичные ситуации возникают при потребности воспользоваться телефонной связью, выполнении программы на компьютере, прохождении платежей в организации, реализация операций кредитования с учетом задержки возврата кредита и т.д. Ремонтные, медицинские службы, вокзалы, аэропорты, банки – все относится к СМО.

СМО можно описать, если задать следующие характеристики:

1. входящий поток требований или заявок, которые поступают на обслуживание

2. дисциплину постановки в очередь и выбор из нее

3. правила, по которым осуществляется обслуживание

4. выходящий поток требований

5. режимы работы

1. Входящий поток. Для задания входящего потока требований необходимо описать моменты времени поступления их в систему (закон поступления) и количество требований, которое поступило одновременно. Закон поступления может быть детерминированный и вероятностный.

В общем случае входящий поток требований описывается распределением вероятности интервала времени между соседними требованиями. Эти интервалы часто полагают одинаково распределенными. При этом поток событий считают стационарным.

generate 5,2

Процесс называется стационарным, если его статистические характеристики не зависят от времени.

Классическая теория СМО рассматривает так называемый простейший (Пуассоновский) поток требований. Для этого потока число требований k для любого интервала времени t распределено по закону Пуассона:

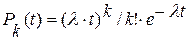
k ≥ 0, t ≥ 0, 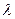- интенсивность потока, т.е. число требований за единицу времени.

Простейший поток обладает следующими свойствами:

1) ординарность, т.е. вероятность того, что в один момент времени придет более одной заявки, пренебрежимо мала

2) отсутствие последствий, т.е. вероятность появления события не зависит от того, сколько и когда событий было ранее

3) стационарность, т.е. характеристики потока не зависят от положения на абсолютной временной оси, а зависят только от разности моментов времени ∆t.

- корреляционная функция;

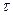= ∆ t = t₁ – t₂

R (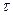) = R (t₁ – t₂)

На практике обоснованием того, что входящий поток требований имеет распределение Пуассона является то, что требования поступают от большого числа источников независимых между собой за определенный интервал времени. При этом эти источники могут иметь произвольное распределение.

Дисциплины постановки в очередь и выбор из нее определяют порядок постановки требований в очередь, если заняты устройства обслуживания и порядок выбора из очереди, если освобождаются обслуживающие устройства. Простейшая дисциплина – «раньше поступил – раньше обслужился» (РПРО и FIFO).

Организация в очереди поп правилу последний поступил – первый обслужился (ПППО или LIFO).

Правило выбора из очереди может быть случайным RANDOM. Возможна также организация выбора из очереди по параметрам. Например, женщины пропускают мужчин вперед в очереди. На очередь могут накладываться ограничения по длине очереди или по времени пребывания в ней.

Очередь может быть с ограниченным количеством мест ожиданий в ней. Это так называемый буфер (например, бункер, в который заготовки поступают раньше, чем могут быть обработаны станком).

Правила обслуживания характеризуются длительностью обслуживания (распределением времени обслуживания), количеством требований, обслуживаемых одновременно и дисциплиной обслуживания. Организация обслуживания может осуществляться с помощью одного устройства – системы с одним устройством (каналом) обслуживания или с несколькими идентичными устройствами. Такие системы называются многоканальными системами. Если устройства обслуживания объединены в последовательную цепочку, то они образуют многофазные системы обслуживания, в которых требования последовательно проходят несколько фаз обслуживания перед тем как покинуть систему. Пример: сборочный конвейер.

Дисциплины обслуживания определяют, при каких условиях прекращается обслуживание требований, как выбирается для обслуживания следующее требование и что делать с частично обслуженным требованием.

Различают бесприоритетные и приоритетные дисциплины. При бесприоритетном обслуживании порядок обслуживания определяется дисциплиной выбора из очереди, при приоритетном обслуживании требованию задается некоторый параметр, который определяет его приоритет. Этот параметр может задаваться в числовом виде (статический приоритет) или в виде функции, которая зависит от времени пребывания в системе (динамический приоритет). Дисциплины обслуживания могут быть с относительными или абсолютными приоритетами. Относительный приоритет предусматривает, что поступление требования с более высоким приоритетом не прерывает обслуживания менее приоритетного требования (обслуживание без прерывания). Из требований с одинаковыми приоритетами может образовываться очередь.

Выходящий поток – поток требований, которые покидают систему. Причем требования могут быть как обслуженные, так и не обслуженные.

Данный поток имеет особое значение для многофазных систем, в которых этот поток становится входящим для других систем. Распределение требований в выходящем потоке зависит как от характеристик входного потока, так и от распределения времени обслуживания в устройстве.

Из теории систем массового обслуживания известно, что выходящий поток из системы с m устройствами с ожиданием при простейшем входном потоке с параметром 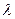и экспоненциальным временем распределения в обслуживаемых устройствах с параметром 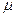есть простейший поток с параметром

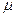_вых = min (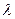, m×m).

Это утверждение дает возможность рассматривать входящий поток как выходной поток из другой системы массового обслуживания. Только для этого случая в теории СМО удалось получить аналитические зависимости. В остальных случаях приходится прибегать к имитационному моделированию процессов.

Для любого типа СМО справедлив так называемый закон Литтла. Для любого распределения времени между двумя событиями поступления требований, любого распределения времени их обслуживания, любого количества устройств обслуживания и любой дисциплины обслуживания среднее количество требований 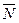в СМО определяется через интенсивность поступления 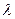и среднее время пребывания требований в системе Т, т.е. 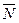= 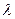Т. Очевидно, это справедливо для стационарного состояния.

Дата добавления: 2014-01-07