Метод Монте-Карло. Вероятностное моделирование

Вероятностное моделирование

В тех случаях, когда при моделировании необходимо учитывать некоторый случайный фактор (элемент или явление), например, риск вложения средств, который невозможно описать аналитически, используют метод моделирования, называемый методом статистических испытаний или методом Монте-Карло.

С помощью этого метода может быть решена любая вероятностная задача, однако использовать его целесообразно в том случае, если решить задачу с его помощью проще, чем любым другим методом. Сущность метода состоит в том, что вместо описания случайных явлений аналитическими зависимостями производится розыгрыш случайных явлений с помощью некоторой процедуры (бросание монеты, кубика, использование генератора случайных чисел), которая дает случайный результат. С помощью розыгрыша получают одну реализацию случайного явления. Проводя многократно такой розыгрыш, накапливают статистический материал, который потом обрабатывают различными методами.

Рассмотрим данный метод на примере вычисления площади плоской фигуры, т.е. данный метод можно применять и для решения не только вероятностных, но и детерминированных задач:

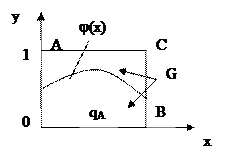Примем для простоты, что ОА=ОВ=1 и будем считать, что 0 ≤ φ(х) ≤ 1. Пусть мы имеем случайную величину Z, равномерно распределенную в интервале [0, 1]. Если величинам x и y приписывать значения пар Z_i, Z_i+1, то пары x и y образуют случайную точку на плоскости XOY. Эти точки будут иметь равномерное распределение внутри квадрата ОАВС. Выборка каждой очередной пары Z_i, Z_i+1 соответствует, таким образом, ”бросанию” точки внутрь квадрата ОАВС.

Пусть всего брошено N точек, из них m_А попало под кривую φ(х), тогда статистическую оценку 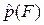вероятности р(F) попадания в область q_a можно найти как отношение: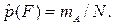

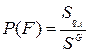- геометрическая интерпретация.

Учитывая, что 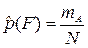и то, что S_G=1, можем записать, что вероятность попадания 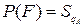, тогда, используя геометрический смысл интеграла, запишем: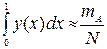

Процедура решения задачи на ЭВМ имеет вид:

1) Выбирается случайное число Z_i на отрезке от 0 до 1 с равномерным законом распределения. Это число принимается равным x_{i .}

2) Вычисляется значение φ(х_i).

3) Вырабатывается очередное число Z_i+1, которое принимается в качестве координаты y_i этой случайной точки: y_i = φ(х_i).

4) Значение φ(х_i) сравнивается с числом Z_i+1. Если φ(х_i+1)³ Z_i+1, то результату сравнения присваивается признак w=1 при φ(х_i+1)< Z_i+1 w=0.

5) Полученное значение признака w добавляется в содержимое счетчика точек под кривой φ(х).

6) Содержимому счетчика числа N добавляется 1.

7) Управление передается к первой операции.

Рассмотренная процедура не требует запоминания всех случайных чисел, полученных в результате эксперимента. Запоминаются лишь числа m_А и N. Это обстоятельство является важной и отличительной особенностью метода Монте-Карло.

Дата добавления: 2014-01-07