КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерий Рауса
|
|
|
|
Критерий Рауса предложен в 1877 году английским математиком Э.Дж. Раусом. Критерий Рауса широко используется при оценке устойчивости систем высокого порядка, если известны и положительны коэффициенты характеристического уравнения. Этот критерий устойчивости просто реализуется на ЭВМ и можно использовать для выяснения влияния коэффициентов уравнения на устойчивость системы.
Применение критерия Рауса требует составления таблицы, представленной в табл. 4.1:
Таблица 4.1.
Таблица Рауса
| Вспомогательные коэффициенты | Номер строки | Номер столбца | |||
| I | II | III | … | ||
| - | 1 | с11=a0 | с12=a2 | с13=a4 | … |
| - | 2 | с21=a1 | с22=a3 | с23=a5 | … |
| r3 | 3 | с31 | с32 | с33 | … |
| r4 | 4 | с41 | с42 | с43 | … |
| … | … | … | … | … | … |
| ri | i | сi1 | сi2 | сi3 | … |
| … | … | … | … | … | … |
| rn+1 | n+1 | сn+1,1 | - | - | … |
Таблица Рауса строится следующим образом:
- в первую строку записывают четные коэффициенты характеристического уравнения, начиная с а0;
- во вторую строку записывают нечетные коэффициенты характеристического уравнения, начиная с а1;
- элементы столбцов, начиная с третьей строки, определяются по выражению:
, (4.7)
где 
; k =1,2,3,…; ri – вспомогательные коэффициенты, определяемые по выражению
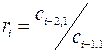, (4.8)
где .
Система устойчива по критерию Рауса, если положительны все коэффициенты первого столбца таблицы Рауса, включая а0 и а1. Если не все коэффициенты положительны, то система неустойчива. При этом число перемен знака среди этих коэффициентов соответствует числу правых корней характеристического уравнения.
Достоинством критериев Гурвица и Рауса является то, что с их помощью можно оценивать устойчивость как замкнутых, так и разомкнутых систем.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 322; Нарушение авторских прав?; Мы поможем в написании вашей работы!