Запасы устойчивости систем автоматического регулирования

Для нормального функционирования САР должна быть достаточно удалена от границы устойчивости и иметь достаточный запас устойчивости, что определяется следующими причинами:

- уравнения элементов САР, как правило, идеализированы, т.е. при их составлении не учтены второстепенные факторы;

- при линеаризации уравнений погрешности дополнительно увеличиваются;

- параметры элементов определяются с некоторой погрешностью;

- параметры однотипных элементов имеют технологический разброс;

- при эксплуатации параметры элементов изменяются вследствие старения.

О запасе устойчивости можно судить по расположению корней характеристического уравнения САР на комплексной плоскости корней (рис. 4.12). Чем дальше они отстоят от мнимой оси в левой полуплоскости, тем больше запас устойчивости.

Рис. 4.12. Комплексная плоскость корней

Каждый критерий устойчивости также позволяет определять запас устойчивости системы. Однако, наибольшее применение на практике находит критерий Найквиста. Устойчивость САР зависит от расположения годографа Найквиста относительно критической точки с координатами (-1, j 0). Чем ближе эта кривая проходит от критической точки, тем ближе САР к границе устойчивости.

Для устойчивых САР выделяют запасы устойчивости по амплитуде h и по фазе g.

Запас устойчивости по амплитуде h – это минимальный отрезок, характеризующий расстояние между критической точкой и ближайшей точкой пересечения годографом Найквиста вещественной оси на отрезке [0, -1] (рис. 4.13).

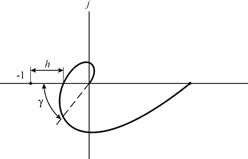
Рис.4.13. Определение запасов устойчивости по критерию Найквиста

Запас устойчивости по фазе g - это минимальный угол, образуемый радиусом, проходящим через точку пересечения годографа Найквиста с окружностью единичного радиуса с центром в начале координат и отрицательной вещественной полуосью.

Система обладает необходимым запасом устойчивости, если она удовлетворяет условию устойчивости и имеет значение модуля 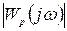, отличающееся от единицы не менее, чем на заданную величину h (запас устойчивости по амплитуде) и угол поворота или фазу, отличающуюся от (-p) не менее, чем на величину g (запас устойчивости по фазе) (рис. 4.14).

Рис.4.14. Требуемые запасы устойчивости САР

В случае применения логарифмического критерия для анализа устойчивости САР запасы устойчивости определяются по логарифмическим частотным характеристикам, так как показано на рис. 4.15.

Рис.4.15. Определение запасов устойчивости по логарифмическим частотным характеристикам

Запасу устойчивости САР по амплитуде соответствует отрезок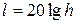

при том значении частоты, при котором ЛФЧХ . Запасу устойчивости по фазе соответствует значение угла между ЛФЧХ и линией -p при частоте среза w_с.

Дата добавления: 2014-01-07