
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Абстрактный интерпретатор логических программ
|
|
|
|
Мы пересмотрим абстрактный интерпретатор, описанный ранее, в свете алгоритма унификации. В результате будет построена полная вычислительная модель логических программ. Все ранее введенные понятия, такие, как редукция цели и протокол вычисления, имеют соответствующие аналоги в полной модели.
Неформально процесс вычисления логической программы может быть описан следующим образом.Он начинается с некоторого исходного (возможно, конъюнктивного) вопроса G и завершается одним из двух результатов: успешное завершение или отказ. В случае успешного завершения результатом должен быть доказанный пример G. Для данного вопроса может существовать несколько успешных вычислений, дающих различные результаты. Кроме того, могут иметь место бесконечные вычисления, с которыми мы не связываем никаких результатов.
Вычисление развивается с помощью редукции целей. На каждом этапе имеется некоторая резольвента, т.е. конъюнкция целей, которые следует доказать. Выбираются такая цель в резольвенте и такое предложение в логической программе, что заголовок предложения унифицируем с целью. Вычисление продолжается с новой резольвентой, полученной из старой заменой выбранной цели на тело раннего предложения и последующим применением наибольшего общего унификатора заголовка предложения и выбранной цели. Вычисление завершается, если резольвента пуста. В этом случае мы говорим, что цель решена программой.
Для более формального описания вычислений введем несколько полезных понятий. Вычислением цели Q = Q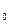 программой Р называется, возможно бесконечная последовательность троек <Q
программой Р называется, возможно бесконечная последовательность троек <Q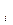 , G
, G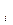 , C
, C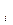 > здесь Q
> здесь Q 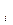 , –конъюнктивная цель, G
, –конъюнктивная цель, G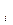 – цель, входящая в Q
– цель, входящая в Q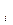 , C
, C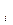 – предложение A¬B
– предложение A¬B …B
…B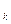 , с таким переименованием, что новые символы переменных не встречаются в Q
, с таким переименованием, что новые символы переменных не встречаются в Q , 0£j£1. Для всех i > 0 цель Q
, 0£j£1. Для всех i > 0 цель Q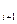 является или результатом замены G
является или результатом замены G , на тело С, в Q
, на тело С, в Q  , и применения подстановки Q
, и применения подстановки Q , наибольшего общего унификатора термов G
, наибольшего общего унификатора термов G  , и А
, и А  , (А
, (А заголовок С
заголовок С ), или константой true, если G
), или константой true, если G – единственная цель в Q
– единственная цель в Q , и тело С
, и тело С  , пусто,или константой отказ если С
, пусто,или константой отказ если С  , и заголовок С
, и заголовок С  , не унифицируемы.
, не унифицируемы.
Цели B  Θ
Θ называются производными от цели G
называются производными от цели G и правила С
и правила С . Цель Gj = B
. Цель Gj = B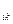 , где B
, где B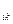 входит в тело предложения С
входит в тело предложения С , называется порожденной G
, называется порожденной G , и С
, и С . Цель G
. Цель G называется предшественником любой порожденной ею цели. Две цели с общим предшественником называются родственными целями.
называется предшественником любой порожденной ею цели. Две цели с общим предшественником называются родственными целями.
Протоколом вычисления (Q , G
, G , C
, C ) логической программы называется последовательность пар <G
) логической программы называется последовательность пар <G ,Θ
,Θ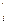 >, где Θ
>, где Θ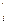 – подмножество н.о.у. Θ
– подмножество н.о.у. Θ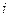 , полученного на i-й редукции и ограниченного переменными из G.
, полученного на i-й редукции и ограниченного переменными из G.
Опишем абстрактный интерпретатор логических программ. Он является модификацией интерпретатора основных целей (рис. 1.1). Ограничение, состоящее в использовании основных примеров предложений при выполнении редукций, теперь снято. Вместо этого алгоритм унификации, примененный к выбранной цели и заголовку выбранного предложения, выбирает корректную подстановку для применения к новой резольвенте.
Следует позаботиться об избежании конфликта имен переменных в правилах. Дело в том, что переменные в предложениях локальны. Поэтому переменные с одними и теми же именами, входящие в различные предложения, на самом деле различны. Это различие обеспечивается переименованием переменных в предложении всякий раз, когда предложение выбрано для выполнения редукции. Среди новых имен не должно быть имен, ранее использованных в процессе вычисления.
Пересмотренная версия интерпретатора приведена на рис. 4.2. Интерпретатор решает вопрос G с помощью программы Р. Результатом работы интерпретатора будет пример G, если найдено доказательство такого примера, или отказ, если в процессе вычисления возник отказ. Заметим, что интерпретатор может и отказаться закончить вычисления.
Вход: Логическая программа Р
цель G
Результат: GΘ, если это пример G, выводимый из Р, или отказ, если возник отказ
Алгоритм: Начальная резольвента равна входной цели G
Пока резольвента непуста, выполнить
Выбрать такую цель А из резольвенты и такое (переименованное) предложение
А '¬ В , В
, В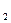 ,..., B
,..., B , п ³ 0 из Р, что А и А' унифицируемы с н.о.у. Θ
, п ³ 0 из Р, что А и А' унифицируемы с н.о.у. Θ
(если нет таких цели и правила, то выйти из цикла).
Удалить А и добавить В ,В
,В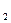 ,...,B
,...,B , к резольвенте.
, к резольвенте.
Применить Θ к резольвенте и к G.
Если резольвента пуста, то результат – G,
иначе результат – отказ.
Рис. 4.2. Абстрактный интерпретатор логических программ.
Пример вопроса, для которого найдено доказательство, называется решением вопроса.
Метод, в соответствии с которым добавляются и удаляются цели в резольвентах, называется методом расписания интерпретатора. В абстрактном интерпретаторе метод расписания не уточнен.
В некоторых вычислениях на каждом шаге вычисления может быть использовано ровно одно предложение программы для редукции очередной цели. Такие вычисления называются детерминированными. Детерминированность вычисления означает, что нам не придется заниматься недетерминированным угадыванием.
Альтернативные выборы, которые может сделать абстрактный интерпретатор при попытке доказать цель, неявно определяют дерево поиска. Если в дереве поиска существует путь, соответствующий доказательству цели, то интерпретатор «угадывает» этот путь. Однако могут быть построены и менее «умные», лишенные способности угадывать интерпретаторы, но обладающие теми же возможностями, что и абстрактный интерпретатор. Один из способов исследования дерева поиска состоит в поиске в ширину, т. е. в параллельном рассмотрении всех возможных выборов. Этот способ гарантирует, что если существует конечное доказательство цели (т.е. конечный успешный путь в дереве поиска), то оно будет найдено.
Другой возможный способ исследования дерева поиска состоит в поиске в глубину. В отличие от поиска в ширину поиск в глубину не гарантирует нахождения доказательства, даже если оно существует. Это объясняется тем, что дерево поиска может содержать бесконечные пути, соответствующие потенциально бесконечным вычислениям недетерминированного интерпретатора. Поиск в глубину может попасть на бесконечный путь и никогда не обнаружить конечного успешного пути, даже если такой путь существует.
Говоря формально, поиск в ширину определяет полную процедуру доказательства логических программ, а поиск в глубину – неполную процедуру. Несмотря на неполноту, в реализациях языка Пролог используется поиск в глубину, что объясняется практическими соображениями.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 515; Нарушение авторских прав?; Мы поможем в написании вашей работы!