Деревья поиска

В рассматривавшихся до сих порвычислениях логических программ проблема недетерминизма всегда разрешалась корректным выбором. Например, в мерах сложности, основанных на дереве доказательства, предполагалось, что для проведения редукциииз программы может быть выбрано нужное предложение. Другой способ вычислительного моделирования недетерминизма состоит в параллельном рассмотрении всех возможных редукций. В этом разделе мы рассмотрим деревья поиска – формализм, подходящий для исследования всевозможных путей вычисления.

Дерево поиска цели G относительно программы Р определяется следующим образом. Корнем дерева является G. Вершины дерева образуют цели (возможно, конъюнктивные) с одной выделенной целью. Для каждого предложения, заголовок которого унифицируем с целью, выделенной в вершине N, имеется ребро, ведущее из вершины N. Каждая ветвь дерева соответствует вычислению цели G относительно программы Р. Листья дерева называются успешными вершинами, если цель, соответствующая листу, пуста, и безуспешными вершинами, если, цель, выделенная в вершине, не может быть редуцирована. Успешные вершины соответствуют решениям корня дерева.

В общем случае для одной и той же цели и одной и той же программы имеется много деревьев поиска.На рис. 5.2 приведены два дерева поиска при решении вопроса сын (S,аран)? с помощью программы 1.2. Два дерева соответствуют двум выборам цели для редукции в резольвенте отец(аран,S), мужчина(S). Деревья различны, но в обоих – единственная успешная ветвь, соответствующая решению вопроса, – S = лот. Соответствующие успешные ветви приведены в виде протоколов на рис. 4.4.

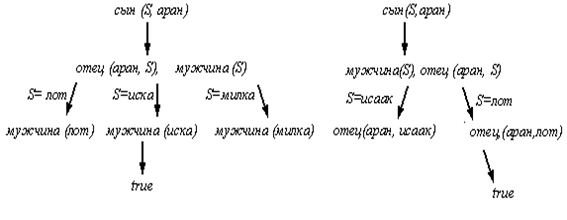
Рис. 5.2. Два дерева поиска.

Мы придерживаемся некоторых соглашений при изображении деревьев поиска. Самая левая цель в вершине всегда выделена. Следовательно, в производных целях цели могут быть переставлены так, чтобы первой стояла цель, выбранная для редукции. На ребрах дерева записываются подстановки, применяемые к переменным самой левой цели. Эти подстановки вычисляются в процессе работы алгоритма унификации.

В случае детерминированных вычислений деревья поиска тесно связаны с протоколами вычислений. Протоколы вычислений аррепd- целей и hanoi -целей, приведенные соответственно на рис. 4.3 и 4.5, могут быть легко преобразованы в деревья поиска.

Дерево поиска содержит несколько успешных вершин, если вопрос имеет несколько успешных решений. На рис. 5.3приведено дерево поиска для вопроса append(As,Bs,[a,b,c]) относительно программы 3.15, определяющей отношение append. Вопрос состоит в расщеплении списка [a,b,c] на два списка. Совокупность меток на ребрах, ведущих в успешную вершину, задаетрешения для As и Вs. Например, самая левая ветвь дерева на рисунке соответствует решению { Аs = [a,b,c], Bs = [ ]}.

Число успешных вершин в различных деревьях поиска для данной цели и данной программы одинаково.

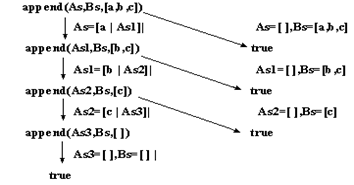
Рис. 5.3. Дерево поиска с многочисленными успешными вершинами.

Дерево поиска может иметь бесконечные ветви, которые соответствуют незавершающимся вычислениям. Рассмотрим цель append(Xs,[c,d],Ys) относительно обычной программы, задающей отношение append. Дерево поиска приведено на рис. 5.4, Бесконечная ветвь соответствует незавершающемуся вычислению, показанному на рис. 4.6

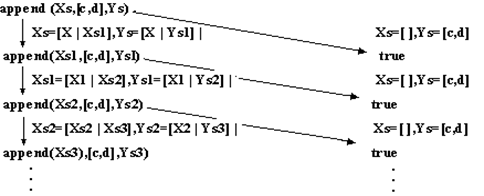
Рис. 5.4. Дерево поиска с бесконечной ветвью.

В терминах деревьев поиска можно определять меры сложности. В программах на Прологе применяется обход дерева в глубину. Поэтому меры сложности, основанные на размере дерева поиска, точнее отражают реальную сложность программ на Прологе, чем меры, основанные на сложности дерева вывода. Однако анализировать сложность дерева поиска гораздо труднее.

Данный вопрос связан с серьезной проблемой. Дело в том, что взаимосвязь между деревьями поиска и деревьями вывода отражает взаимосвязь между детерминированными и недетерминированными вычислениями. Вопрос о совпадении классов сложности, определяемых в терминах деревьев вывода, с классами сложности, определяемыми в терминах деревьев поиска, является классическим вопросом «Р =NP», переформулированным в терминах логического программирования.

Дата добавления: 2014-01-07