
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В замкнутой системе
|
|
|
|
МЕХАНИЧЕСКИЕ НЕЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Лекция
Колебательное движение, или просто колебания, - это движение, характеризуемое повторяемостью во времени значений физических величин, определяющих это движение. С колебаниями мы встречаемся при изучении различных физических явлений: звука, света, переменного тока, радиоволн, качаний маятника и т.д. Оказывается, что существует общность закономерностей этих явлений и математических методов исследования. Поэтому основные законы теории механических колебаний должны послужить прочным фундаментом для изучения различных видов колебаний в последующих разделах физики.
Рассмотрим колебания, происходящие под действием упругой силы, например, колебания пружинного маятника. Такая система называется линейным гармоническим осциллятором. Пружинный маятник состоит из массивного шара, насаженного на горизонтальный стержень, вдоль которого шар может скользить. На стержень надета пружина, закрепленная на его конце и на шаре (рис 1). Массой пружины по сравнению с массой шара можно пренебречь. 
В состоянии покоя шар находится в положении 1 (пружина недеформирована). Если перевести шар в положение 2 (пружина растянута вдоль горизонтальной оси на величину х), появляется упругая сила, подчиняющаяся закону Гука: 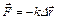 , где
, где  - перемещение шара, k – коэффициент жесткости пружины. Упругая сила всегда противоположна по направлению вектору перемещения маятника (
- перемещение шара, k – коэффициент жесткости пружины. Упругая сила всегда противоположна по направлению вектору перемещения маятника ( ). Если отпустить шар, то он под действием упругой силы начнет ускоренно двигаться влево. Применим к движению шара второй закон Ньютона и запишем его в проекциях на ось Х:
). Если отпустить шар, то он под действием упругой силы начнет ускоренно двигаться влево. Применим к движению шара второй закон Ньютона и запишем его в проекциях на ось Х:
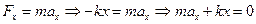 . Или, выразив ускорение, получим:
. Или, выразив ускорение, получим:
|
|
|
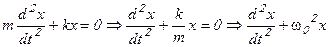 , (3.1)
, (3.1)
где 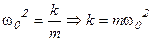
Решение однородного дифференциального уравнения второго порядка имеет вид:
 , (3.2)
, (3.2)
где Х - смещение маятника от положения равновесия в любой момент времени;
A – амплитуда колебания маятника, его максимальное отклонение от положения равновесия.
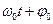 -фаза колебания, величина, которая определяет положение маятника в любой момент времени;
-фаза колебания, величина, которая определяет положение маятника в любой момент времени;
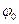 - начальная фаза колебания, характеризующая положение маятника в начальный момент движения;
- начальная фаза колебания, характеризующая положение маятника в начальный момент движения;
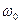 - циклическая частота колебаний, она связана с периодом колебания по уравнению
- циклическая частота колебаний, она связана с периодом колебания по уравнению 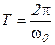 и с линейной частотой колебаний
и с линейной частотой колебаний  . Линейная частота – это число полных колебаний в единицу времени -
. Линейная частота – это число полных колебаний в единицу времени - .
.
Теперь можно выразить скорость шара (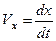 ) и его ускорение (
) и его ускорение (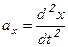 ) при колебательном движении:
) при колебательном движении:

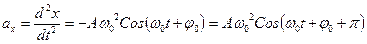 . (3.3).
. (3.3).
Полученные уравнения (3.1), (3.2) и (3.3) показывают, что все кинематические величины – смешение, скорость, ускорение, характеризующие колебания маятника:
- изменяются со временем по одинаковому закону – гармоническому;
- имеют одинаковую частоту колебаний и одинаковый период;
- амплитуды этих величин, т.е. их максимальные значения, различны:
для смещения Х – А; для скорости  -
- 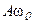 ; для ускорения
; для ускорения 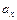 -
- 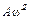 ;
;
- по фазе колебания эти величины смещены относительно друг друга:
скорость (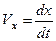 )на
)на 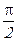 относительно смещения маятника Х, т.е. когда маятник находится в положении максимального отклонения от положения равновесия -
относительно смещения маятника Х, т.е. когда маятник находится в положении максимального отклонения от положения равновесия - 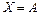 , его скорость равна нулю;
, его скорость равна нулю;
ускорение (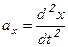 ) на
) на 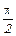 , относительно скорости, т.е. если скорость маятника равна нулю, то ускорение достигает максимальной величины -
, относительно скорости, т.е. если скорость маятника равна нулю, то ускорение достигает максимальной величины - 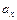 -
-  (рис.2).
(рис.2). 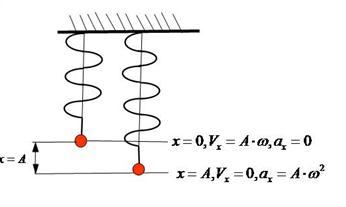
Полная энергия маятника ( ) равна сумме кинетической энергии шара (
) равна сумме кинетической энергии шара (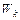 ) и потенциальной энергии упруго деформированной пружины (
) и потенциальной энергии упруго деформированной пружины (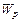 ): Запишем соответствующие уравнения и, сложив их, определим полную энергию:
): Запишем соответствующие уравнения и, сложив их, определим полную энергию:

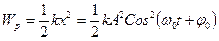
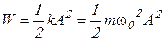 (3.4).
(3.4).
Построим графики зависимости от времени кинетической, потенциальной и полной энергии (примем, что 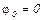 ) и проанализируем их (рис 3).
) и проанализируем их (рис 3). 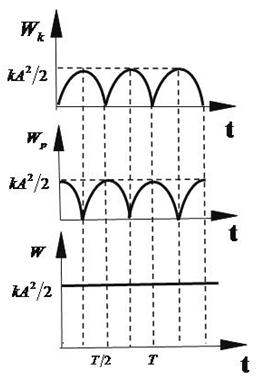
|
|
|
В те моменты времени, когда кинетическая энергия достигает максимального значения, потенциальная равна нулю и наоборот. При этом во все моменты времени полная энергия маятника остается постоянной. Её численное значение пропорционально квадрату амплитуды колебания.
Колебания, которые возникают в системе, не подверженной действию внешних сил, называются свободными. Если система консервативна, то при колебаниях не происходит рассеяния механической энергии, т. е механическая энергия системы не превращается в другие виды энергий – она остается постоянной.
В реальном случае часть энергии пружинного маятника будет затрачиваться на работу против сил трения, возникающих при скольжении шара вдоль стержня. Когда вся энергия маятника израсходуется на эту работу, колебания прекратятся.
Кинетическая и потенциальная энергия при свободных незатухающих гармонических колебаниях изменяются периодически. Однако период изменения энергии в два раза меньше периода изменения смещения, скорости, ускорения. За время одного полного колебания кинетическая и потенциальная энергии дважды достигают максимального значения и дважды обращаются в ноль. Это связано с тем, что та и другая энергии пропорциональны квадрату косинуса и синуса фазы колебаний.
Приведем примеры систем, совершающих свободные гармонические колебания.
1. Математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити. Если отклонить маятник от положения равновесия, так чтобы нить составляла небольшой угол с вертикалью и затем его отпустить, то он начнет колебаться в вертикальной плоскости под действием собственного веса (Рис.4).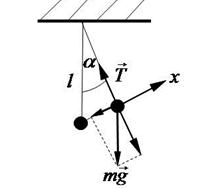
Сила, возвращающая математический маятник в положение равновесия, является составляющей его веса и численно равна:
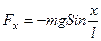 , где m – масса тела; l – длина нити.
, где m – масса тела; l – длина нити.
Если учесть, что для малых углов 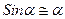 , то
, то
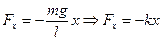 , где
, где  . (3.5)
. (3.5)
Следовательно, период математического маятника можно определить по уравнению 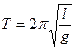 .
.
Таким образом, математический маятник движется под действием силы, которая подобна упругой силе по своему действию - она прямо пропорциональна смещению от положения равновесия и направлена в сторону противоположную перемещению тела. Силы подобные по своему действию упругой силе, но не являющимися таковыми по своей природе, называются квазиупругими.
|
|
|
Запишем уравнение колебаний математического маятника:
 (3.6)
(3.6)
2. Физический маятник – твердое тело, которое может вращаться под действием своей силы тяжести вокруг неподвижной горизонтальной оси (точка О), не проходящей через центр тяжести тела (центр масс) - точка С (Рис. 5).
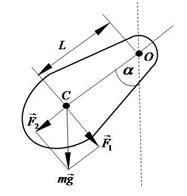 Пусть маятник отклонен от положения равновесия на небольшой угол
Пусть маятник отклонен от положения равновесия на небольшой угол  . Составляющая веса
. Составляющая веса 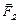 , направленная вдоль ОС, уравновешивается реакцией оси О. Составляющая
, направленная вдоль ОС, уравновешивается реакцией оси О. Составляющая  , перпендикулярная линии ОС, стремится возвратить маятник в положение равновесия. Она численно равна
, перпендикулярная линии ОС, стремится возвратить маятник в положение равновесия. Она численно равна 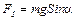 , при малом угле
, при малом угле 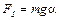 . Возвращающий момент, создаваемый силой
. Возвращающий момент, создаваемый силой  , численно равный
, численно равный 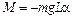 , вызывает ускоренное вращение физического маятника вокруг оси О.
, вызывает ускоренное вращение физического маятника вокруг оси О.
Запишем второй закон Ньютона для тела, вращающегося вокруг неподвижной оси:
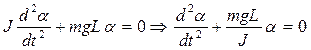 , где
, где 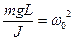 (3.7)
(3.7)
 - момент инерции маятника относительно оси О;
- момент инерции маятника относительно оси О;
L – расстояние между точками О и С.
Период физического маятника (по аналогии с пружинным маятником) можно определить по уравнению:
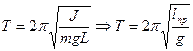 . (3.8)
. (3.8)
 –приведенная длина маятника – длина такого физического маятника, который колеблется с периодом равным периоду математического маятника.
–приведенная длина маятника – длина такого физического маятника, который колеблется с периодом равным периоду математического маятника.
Чтобы определить приведенную длину маятника, приравняем периоды физического и математического маятников:
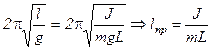 . (3.9)
. (3.9)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 737; Нарушение авторских прав?; Мы поможем в написании вашей работы!