Вынужденные механические колебания

Рассмотрим колебания, которые совершает система, если на неё, кроме упругой силы (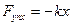) и сил сопротивления (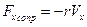), действует еще добавочная периодическая сила (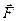), которую назовем вынуждающей или возмущающей силой. Такие колебания совершает, например, груз, подвешенный на пружине и подталкиваемый вверх через равные промежутки времени. Если период колебаний вынуждающей силы не равен периоду свободных колебаний системы, то вначале происходит несколько биений, а затем устанавливаются вынужденные колебания с постоянной амплитудой. Биения, происходящие вначале, являются результатом наложения вынужденных колебаний и свободных затухающих колебаний.

Рассмотрим простейший случай, когда вынуждающая сила изменяется по гармоническому закону:

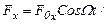
Запишем второй закон Ньютона Рассмотрим колебания, которые совершает система, если на неё, кроме упругой силы (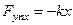) и сил сопротивления (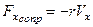), действует еще добавочная периодическая сила (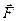), которую назовем вынуждающей или возмущающей силой. Такие колебания совершает, например, груз, подвешенный на пружине и подталкиваемый вверх через равные промежутки времени. Если период колебаний вынуждающей силы не равен периоду свободных колебаний системы, то вначале происходит несколько биений, а затем устанавливаются вынужденные колебания с постоянной для случая, когда действуют упругая сила, сила сопротивления и вынуждающая сила:

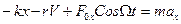
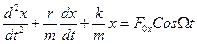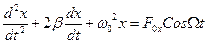. , (3.32)

где величины 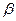и 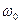имеют тот же смысл, что и в уравнениях (3.2 и 3.25).

Получили дифференциальное уравнение второго порядка неоднородное. Общее решение этого уравнения равно сумме двух решений:

,

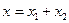где 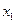- общее решение уравнения (3.32) без правой части, характеризующее затухающие колебания

;

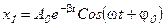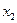- частное решение уравнения (3.32), характеризующее вынужденные колебания

.

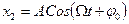Теперь запишем общее решение уравнения (3.32), подставив 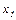и :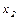

.

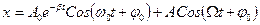При наличии периодической вынуждающей силы материальная точка совершает одновременно и собственные затухающие и вынужденные колебания. Затухающие колебания постепенно прекращаются. Остаются вынужденные колебания. Графики собственных, вынужденных и результирующих колебаний представлены на Рис.16.

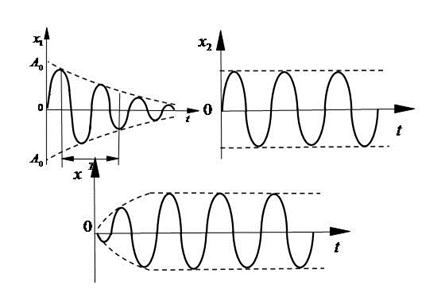
Из уравнения (3.32), произведя соответствующие математические преобразования, можно получить уравнения для установившейся амплитуды вынужденных колебаний и начальной фазы:

(3.33)

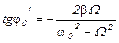(3.34)

Рассмотрим зависимость амплитуды от частоты вынужденных колебаний при фиксированных 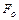,, , 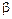и 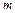, полагая, что затухание мало ():

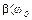если 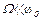имеем, что 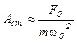- статическое значение амплитуды;

если 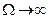. то ;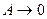

при некотором значении 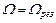амплитуда достигает максимума. Эта частота называется РЕЗОНАНСНОЙ частотой и может быть рассчитана по уравнению:

(3.35)

Подставив 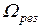в уравнение (3.33), получим выражение для максимальной амплитуды вынужденных колебаний:

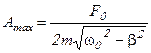(3.36)

Дата добавления: 2014-01-07