Идеального газа для давления

Основное уравнение молекулярно-кинетической теории

Два метода изучения вещества

Молекулярно-кинетический метод ставит своей задачей объяснить макроскопические свойства тел путем детального разбора тех молекулярных процессов, которые лежат в их основе. Так давление газа обусловлено ударами отдельных молекул о стенки сосуда. Постоянство давления при данных условиях есть результат того, что измеряя давление, мы наблюдаем средний эффект ударов очень большого числа молекул за промежуток времени, весьма большой по сравнению со временем отдельного удара.

Беспорядочность движения молекул приводит к наличию определенных закономерностей. Так, формула распределения скоростей Максвелла показывает, что среди беспорядочных значений скоростей существует наиболее вероятная скорость, т.е. такая скорость, значительные отличия от которой встречаются редко. Кинетическая энергия молекул может принимать самые разнообразные значения в данном равновесном состоянии. Средняя же энергия при этом имеет определенное значение. Эта средняя энергия определяет температуру тела.

Таким образом, макроскопические величины обладают определенными значениями лишь потому, что они являются средним значением очень большого числа отдельных элементарных процессов. Молекулярно-кинетический метод есть по существу статистический метод.

Термодинамический метод – описывает поведение системы, не входя в детальное рассмотрение молекулярных процессов, и при этом позволяет делать ряд выводов относительно их протекания, столь же достоверных, как и те фундаментальные законы, которые лежат в основе термодинамики. Такое рассмотрение возможно, благодаря введению понятий об энергии, её превращениях, способах передачи и установлению тех законов, которым подчиняются эти превращения энергии из одних видов в другие.

Термодинамический метод, относящийся к энергетической стороне процессов, имеет большое практическое значение. Обширный класс технических проблем, связанный с переходом энергии из одной формы в другую и с получением за счет энергии работы, может быть разобран с термодинамической точки зрения.

Законы, лежащие в основе термодинамики, носят название начал термодинамики. Эти начала установлены как обобщение экспериментальных данных; их достоверность подтверждается в дальнейшем совпадении большого числа выводов из них с результатами опытов.

Впервые объяснение давления газа на стенки сосуда, как результат ударов отдельных молекул, было выдвинуто петербургским академиком Даниилом Бернулли в 1738 г.

Представим сосуд в виде куба со стороной , в котором беспорядочно движется 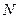молекул идеального газа (Рис.1).

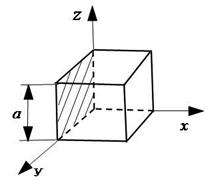
Разные молекулы движутся с разными скоростями. Определим то давление, которое молекулы газа оказывают на заштрихованную стенку. В направлении этой стенки движется одна треть от общего количества молекул -. Рассмотрим взаимодействие молекулы идеального газа со стенкой. Отдельная молекула, летящая перпендикулярно к выделенной стенке, согласно второму закону Ньютона, изменяет свой импульс:

,

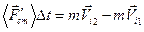где 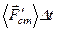- импульс средней силы, действующей со стороны стенки на молекулу; - время удара; 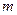- масса молекулы; .

По третьему закону Ньютона со стороны молекулы на стенку будет действовать сила , численно равная силе, действующей со стороны стенки, и противоположно ей направленная, следовательно, импульсы этих сил тоже будут равны и направлены в противоположные стороны (Рис.2).

Спроектировав вектора на выбранную ось, получим:

,

где- изменение импульса одной молекулы при каждом её столкновении со стенкой.

Отскочив от стенки, молекула, полетит к противоположной стенке и, отскочив, в свою очередь, от неё, снова вернется к первой за время - 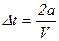. Выразим силу, действующую со стороны одной молекулы на стенку сосуда:

.

Теперь рассчитаем силу, которая действует на выделенную стенку со стороны молекул движущихся перпендикулярно к этой стенке. Необходимо помнить, что разные молекулы имеют разные скорости. Вынося, постоянные величины за знак суммы и введя два сомножителя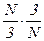, получаем квадрат средней квадратичной скорости -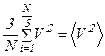. Тогда сила, действующая на отмеченную стенку со стороны 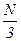молекул, движущихся перпендикулярно выделенной стенке, равна:

.

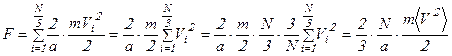Зная силу, определим давление на отмеченную стенку:

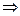
(4.1)

где - концентрация молекул идеального газа в сосуде;

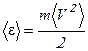- средняя кинетическая энергия одной молекулы при её поступательном движении.

Полученное уравнение (4.1) называется ОСНОВНЫМ УРАВНЕНИЕМ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА, или уравнением Клаузиуса.

Дата добавления: 2014-01-07