Таким образом, макропараметр системы – давление газа – определяется через кинетическую энергию одной молекулы и количество молекул газа

Выведем ряд следствий из основного уравнения МКТ.

1. Заменим среднюю кинетическую энергию молекулы, воспользовавшись соотношением .

Уравнение (4.1) принимает вид - . (4.2)

2. Допустим, что имеем смесь газов (например, воздух). В этом случае концентрацию молекул газовой смеси следует записать, как сумму концентраций молекул газов, входящих в смесь - 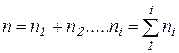. Уравнение (4.1) принимает вид:

или (4.3)

где - парциальное давление газа, входящего в смесь.

Парциальное давление газа, входящего в смесь, - это то давление, которое оказывал бы газ, если бы он занимал объем один. Таким образом, давление смеси газов равно сумме парциальных давлений газов, входящих в смесь.

3. Заменим в уравнении (4.1) концентрацию молекул газа 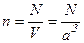, среднюю кинетическую энергию молекулы 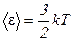; учтем, что и ,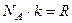

где - газовая постоянная.

Основное уравнение МКТ принимает вид:

. (4.4)

Уравнение (4.4) связывает параметры состояния газа – давление, объем, температуру – и называется уравнением состояния идеального газа.

Состояние газа характеризуется параметрами состояния. Если параметры не изменяются со временем и при этом они одинаковы по всей системе, такое состояние газа называется равновесным. Если газ переходит из одного состояния в другое, то в нем происходит процесс. Процесс будет равновесным, если промежуточные состояния равновесные. Выделяют среди процессов изопроцессы, т.е. процессы, когда один из параметров состояния остается постоянным. Воспользовавшись уравнением состояния, запишем уравнения состояния равновесных изопроцессов и изобразим их графически.

1. Изобарический процесс – это процесс, когда давление газа постоянно ().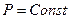

Разделив в уравнении (4.5) постоянные и переменные величины, получим уравнение состояния газа для изобарического процесса:

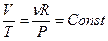или , (4.5)

следовательно, объем и температура газа связаны между собой прямо пропорциональной зависимостью – увеличение объема сопровождается увеличением температуры при постоянном давлении.

Представим изобарический процесс на графиках в координатах , , . Рис.3.

На графике в координатах , согласно уравнению (4.5), . Следовательно, при увеличении давления угол наклона прямой линии уменьшается.

2. Изохорический процесс – это процесс, когда объем газа остается постоянным ().

Разделив в уравнении (4.4) постоянные и переменные величины, получим уравнение состояния газа для изохорического процесса:

или , (4.6)

Давление и температура газа связаны между собой прямо пропорциональной зависимостью – увеличение давление сопровождается увеличением температуры при постоянном объеме.

Представим изохорический процесс на графиках в координатах 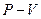, , Рис.4.

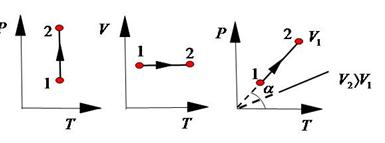
На графике в координатах , согласно уравнению (4.6), . Следовательно, при увеличении объема угол наклона прямой линии уменьшается.

3. Изотермический процесс – это процесс, когда температура газа остается постоянной ().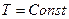

Разделив в уравнении (4.4) постоянные и переменные величины, получим уравнение состояния газа для изотермического процесса:

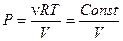или (4.7)

Уравнение (4.7) показывает что, давление и объем газа связаны между собой обратно пропорциональной зависимостью – увеличение давление сопровождается уменьшением объема при постоянной температуре.

Представим изотермический процесс на графиках в координатах 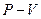, , Рис.5.

На графике в координатах 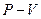, согласно уравнению (4.7), при повышении температуры изотерма будет расположена выше.

Дата добавления: 2014-01-07