Изменение энтропии численно равно количеству теплоты, сообщенной газу, в обратимом процессе деленному на абсолютную температуру тела. Эта величина называется приведенной теплотой

Качественное распределение молекул по системе называется микросостоянием. Число микросостояний, которыми может быть реализовано данное макросостояние, называется термодинамической вероятностью (W). Число непрерывно сменяющих друг друга качественных состояний, другими словами микросостояний, и характеризует степень беспорядочности макросостояния всей системы.

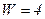Чтобы рассчитать термодинамическую вероятность во всех рассматриваемых случаях пронумеруем молекулы – 1,2,3,4. Термодинамическая вероятность в первом случае равна (Рис.4а); во втором - (Рис.4б); в третьем - 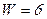(Рис.4в).

Однако, характеризовать степень беспорядочности молекулярного движения с помощью термодинамической вероятности неудобно, так как вероятность величина мультипликативная - термодинамическая вероятность системы равна произведению вероятностей в подсистемах:

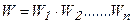
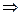
. (6.12).

Рассмотрим один из важнейших циклов – Цикл Карно. Этот цикл сыграл огромную роль в

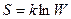. (6.13)

Тогда уравнение энтропии всей системы имеет вид:

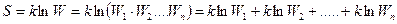, (6.14)

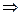
следовательно, 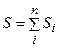(6.15)

Энтропия системы – величина аддитивная - равна сумме энтропий в подсистемах. Энтропия, подобно внутренней энергии, является однозначной функцией состояния системы.

Используя, введенное Больцманом определение энтропии (6.13) как меры беспорядочности молекулярных движений, проанализируем, как ведет себя энтропия при обратимых и необратимых процессах.

Допустим, имеется один моль идеального газа, т.е. 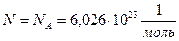, находящийся в объеме 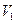. Разделим этот объем на ячейки, в каждую можно поместить лишь одну молекулу. Определим термодинамическую вероятность размещения молекул по ячейкам в объёме 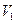, т.е. возможное число микросостояний, с учетом свойства мультипликативности вероятности имеем:

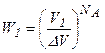
. (6.16)

Соответственно энтропия в исходном состоянии равна:

(6.18)

Увеличим объем, занимаемый газом, до . Молекулы получают возможность попадать в области пространства, ранее им недоступные. Благодаря этому возрастает число различных, возможных микросостояний и степень беспорядка возрастает, т.е. возрастает термодинамическая вероятность и энтропия:

; (6.19)

Определим изменение энтропии в процессе расширения газа, которое представляет количественную меру увеличения степени хаотичности молекулярных движений в данном процессе:

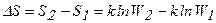. (6.20)

Подставив в уравнение (19), уравнения (17) и (18) получаем:

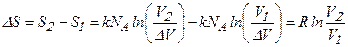. (6.21)

Пусть процесс расширения газа происходил изотермически (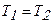) и обратимо. По первому началу термодинамики в случае изотермического процесса вся подводимая теплота расходуется на работу газа, которую можно рассчитать по уравнению:

, если 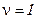. (6.22)

Сравнив уравнения (6.21) и (6.22) получаем:

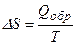, для бесконечно малого изменения энтропии (6.23)

В тех случаях, когда теплота сообщается газу в произвольном процессе, необходимо разбить этот процесс на бесконечно малые участки. Приведенное количество теплоты, сообщенной телу на каждом бесконечно малом участке процесса равна 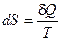, где 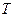- температура соответствующего «источника теплоты». Каждый такой процесс, если он протекает бесконечно медленно, можно считать изотермическим и обратимым. Суммируя эти величины для всех участков произвольного процесса, получим выражение, которое называется интегралом приведенной теплоты:

. (6.24)

.

При всех процессах, происходящих в макроскопических системах, энтропия системы возрастает (необратимые процессы) или остается неизменной (обратимые процессы), т.е. .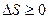

Существует несколько формулировок второго начала, предложенных великими физиками, приведем некоторые из них.

Клазиус Теплота никогда не может переходить сама собой от тел с более низкой температурой к телам с более высокой температурой.

Томсон Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара (передачи тепла от более нагретого тела к менее нагретому телу).

Планк Невозможно построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счет охлаждения резервуара.

Карно Невозможно создать вечный двигатель второго рода.

Дата добавления: 2014-01-07