Теорема Гаусса для электростатического поля

Вычисление напряженности поля системы электрических зарядов с помо­щью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом теорему, опре­деляющую поток вектора напряженности электрического поля через произ­вольную замкнутую поверхность

В соответствии с формулой (1.5) поток вектора напряженности сквозь сфе­рическую поверхность радиуса r, охватывающую точечный заряд Q, находя­щийся в ее центре (рис 6),

.

Этот результат справедлив для замкнутой поверхности любой формы Действительно, если окружить сферу (рис. 6) произвольной замкнутой поверх­ностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность

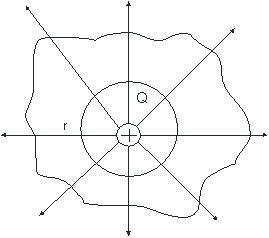
Рис. 6 Рис. 7

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 7), то при пересечении любой выбранной линии напряженности с поверх­ностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, т.к. поток считается положительным, если линии напряженности выходят из по­верхности, и отрицательным для линий, входящих в поверхность.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее ра­вен нулю, т.к. число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и за­ключает в себя точечный заряд Q, поток вектора 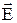будет равен , т.е.

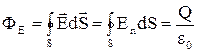. (1.6)

Знак потока совпадает со знаком заряда Q.

Рассмотрим общий случай произвольной поверхности, окружающей n за­рядов. В соответствии с принципом суперпозиции напряженность 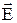поля, соз­даваемого всеми зарядами, равна сумме напряженностей 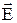_i, создаваемых каж­дым зарядом в отдельности: 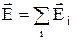. Поэтому

.

Согласно (1.6), каждый из интегралов, стоящий под знаком суммы, равен . Следовательно,

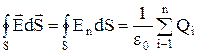. (1.7)

Формула (1.7) выражает теорему Гаусса для электростатического поля в вакууме: "поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри мой поверхности зарядов, деленной на ε₀". Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским, а затем независимо от него применительно к электростатическому полю - К.Гауссом.

Дата добавления: 2014-01-07