Закон Ома. Сопротивление проводников

Немецкий физик Г.Ом экспериментально установил, что сила тока I, теку­щего по однородному металлическому проводнику, т.е. проводнику, в котором не действуют сторонние силы, пропорциональна напряжению U на концах проводника.

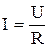, (2.7)

где R - электрическое сопротивление проводника. Уравнение (2.7) выражает з а к о н О м а д л я у ч а с т к а ц е п и (не содержащего источника э.д.с): си­ла тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула (2.7) позволяет установить единицу сопротивления - ОМ (Ом): 1 Ом сопротивление такого проводника, в котором при напряжении в 1 В течет постоянный ток 1 А

Величина 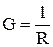называемся э л е к т р и ч е с к о й п р о в о д и м о с т ь ю проводника. Единица проводимости- с и м е н с (См): 1 См - проводимость участка электрической цепи сопротивлением I Ом

Сопротивление проводника зависит от его размеров и формы, а также ма­териала, из которого проводник изготовлен Для однородного линейного про­водника сопротивление R прямо пропорционально его длине l и обратно про­порционально площади его поперечного сечения S:

(2.8)

где ρ - коэффициент пропорциональности, характеризующий материал про­водника. Он называется у д е л ь н ы м э л е к т р и ч е с к и м с о п р о т и в л е н и е м. Единица удельного электрическою сопротивления ом-метр (Ом·м). Наименьшим удельным сопротивлением обладают серебро (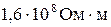) и медь ()

Закон Ома можно представить в дифференциальной форме. Подставив вы­ражение для сопротивления (2.8) в закон Ома (2.7), получим

, (2.9)

где величина

,

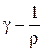обратная удельному сопротивлению, называется у д е л ь н о й э л е к т -р и ч е с к о й п р о в о д и м о с т ь ю вещества проводника. Ее единица - сименс на метр (См/м). Учитывая, что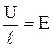- напряженность электрического поля в проводнике, - плотность тока, формулу (2.9) можно записать в виде

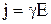. (2.10)

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу (2.10) можно записать в виде

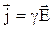. (2.11)

Выражение (2.11) з а к о н О м а в д и ф ф е р е н ц и а л ь н о й ф о р м е, связывающий плотность тока в любой точке внутри проводника с напря­женностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а следовательно, и сопротивления, в зависимости от температуры описывается линейным законом:

,

,

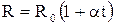где и 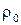, R и R₀ - соответственно удельные сопротивления и сопротивления

проводника при t=0°С, α - т е м п е р a т у р н ы й к о э ф ф и ц и е н т с о п р о т и в л е н и я, для чистых металлов (при не очень низких температурах) близкий к 1/273 Значит, температурная зависимость сопротивления может быть представлена в виде

,

где Е –термодинамическая температура.

Качественная температурная зависимость сопротивления металла пред­ставлена на рис.27 (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например Al, Pb, Zn и др.) и их сплавов при очень низ­ких температурах Т (0,14-20 К), называемых к р и т и ч е с к и м и, характер­ных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становится абсолютным проводником.

Рис. 21

Впервые это явление, называемое сверхпроводимостью обнаружено в 1911году Г.Камерлинг-Оннесом для ртути. Яв­ление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверх проводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруд­нено из-за низких их критических температур. Правда, в настоящее время об­наружены и активно исследуются керамические материалы, обладающие сверх­проводимостью при температуре выше 100 К. На зависимости электрического сопротивления металлов от температуры основано действие т е р м о м е т р о в с о п р о т и в л е н и я, которые позволяют по градуированной взаимосвязи со­противления от температуры измерять температуру с точностью до 0,003 К.

Применение же в качестве рабочего вещества термометра сопротивления полупроводников, приготовленных по специальной технологии,- т е р м и с т о ров- позволяет отмечать изменение температуры в миллионные доли Кель­вин и использовать термисторы для измерения температур в случае малых га­баритов полупроводников.

Дата добавления: 2014-01-07