Разветвленные цепи. Правила Кирxгофа

Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными Кирх­гофом. Этих правил два. Первое из них относится к узлам цепи. У з л о м называется точка, в которой схо­дятся более чем два проводника (рис. 28). Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла - имеющим другой знак (минус или плюс).

Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:

. (2.22)

Это правило вытекает из уравнения непрерывности, т. е., в конечном счете, из закона сохранения заряда. Для по­стоянного тока 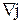всюду равна нулю. Сле­довательно, поток вектора j (т.е. алгебраическая сумма токов, текущих через окружающую узел воображаемую за­мкнутую поверхность) должен быть равен нулю.

Рис. 28 Рис. 29

Уравнение (2.22) можно написать для каждого из N узлов цепи. Однако независимыми являются только N - 1 уравнений, N-e будет следствием из них.

Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (см., например, контур 1-2-3-4-1 на рис. 29). 3ададимся направлением обхода (например, по часовой стрелке, как указано на ри­сунке) и применим к каждому из неразветвленных участ­ков контура закон Ома:

При сложении этих выражений потенциалы взаимно уни­чтожаются и получается уравнение

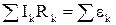, (2.23)

:которое выражает в т о р о е п р а в и л о Кирхгофа.

Уравнение (2.23) может быть составлено для всех за­мкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя полу­чить наложением других контуров один на другой. Так, например, для цепи, изображенной на рис. 30, можно составить три уравнения:

1) для контура 1-2-3-6-1,

2) для контypa 3-4-5-6-3,

3) для контура 1-2-3-4-5-6-1.

Последний контур получается наложением первых двух. Поэтому уравнения не будут независимыми. В качестве независимых можно взять любые два уравнения из трех.

При составлении уравне­ний второго правила Кирхгофа токам и ЭДС нужно приписывать знаки в соответст­вии с выбранным направле­нием обхода. Например, ток I₁ на рис. 30 нужно считать отрицательным, так как ток течет навстречу выбранному направлению обхода. ЭДС ε₁ также нужно приписать знак минус, так как она действует в направлении, противополо­жном направлению обхода, и т. д.

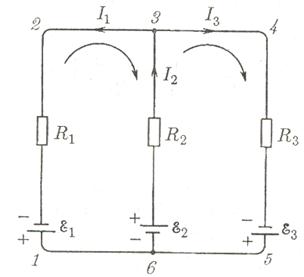Рис. 30

Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от вы­бора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же ЭДС войдет в разные уравнения с различными знаками (так получается с током I2 на рис. 30 при указанных напра­влениях обхода в контурах). Это, однако, не имеет ника­кого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении (2.23) на обратные.

Составляя уравнения, следует помнить, что через лю­бое сечение неразветвленного участка цепи течет один и тот же ток. Например, на участке от точки 6 до источника тока ε₂ течет такой же ток I₂, как на участке от источника до точки 3.

Число независимых уравнений, составленных в соот­ветствии с первым и вторым правилами Кирхгофа, оказы­вается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления для всех неразветвленных участков, то могут быть вычи­слены все ТОRИ. Можно решить и задачу иного рода, на­пример найти ЭДС, которые нужно включить в каждый из участков цепи, чтобы получить при заданных сопротивлениях нужные токи.

Дата добавления: 2014-01-07