Определение минимального количества измерений

Для проведения опытов с заданной точностью и достоверностью необходимо знать то количество измерений, при котором экспериментатор уверен в положительном исходе. В связи с этим одной из первоочередных задач при статических методах оценки является установление минимального, но достаточного числа измерений для данных условий. Задача сводится к установлению минимального объема выборки (числа измерений) при заданных значениях доверительного интервала и доверительной вероятности. При выполнении измерений необходимо знать их точность:

где 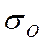- среднеарифметическое значение среднеквадратичного отклонения 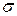, равное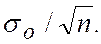

Значение часто называют средней ошибкой. Доверительный интервал ошибки измерения определяется аналогично для измерений 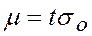. С помощью t легко определить доверительную вероятность ошибки измерений из таблиц.

В исследованиях часто по заданной точности и доверительной вероятности измерения определяют минимальное количество измерений, гарантирующих требуемые значения и .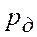

Можно получить

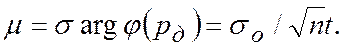
При 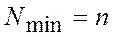получаем

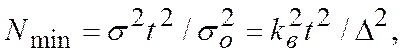
здесь 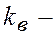- коэффициент вариации (изменчивости), %; 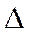- точность измерений, %.

Для определения 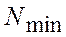может быть принята такая последовательность вычислений:

1) проводится предварительный эксперимент с количеством измерений п, которое составляет в зависимости от трудоемкости опыта от 20 до 50;

2) вычисляется среднеквадратичное отклонение ;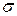

3) в соответствии с поставленными задачами эксперимента устанавливается требуемая точность измерений , которая не должна превышать точности прибора;

4) устанавливается нормированное отклонение t, значение которого обычно задается (зависит также от точности метода);

5) определяют и тогда в дальнейшем в процессе эксперимента число измерений не должно быть меньше .

17. Критерий Стьюдента (Госсета).

Оценки измерений с помощью 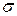и 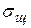по приведенным методам справедливы при п > 30. Для нахождения границы доверительного интервала при малых значениях применяют метод, предложенный английским математиком В.С.Госсетом (псевдоним Стьюдент). Кривые распределения Стьюдента в случае 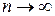(практически при 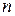>20) переходят в кривые нормального распределения (рис.1).

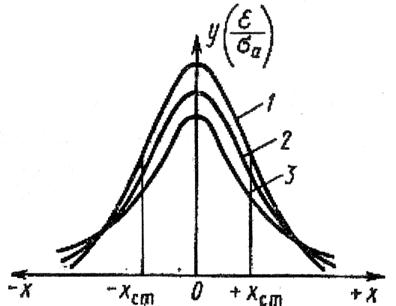
Рис.1. Кривые распределения Стьюдента для различных значений:

1 - 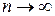; 2 - 3 -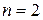

Для малой выборки доверительный интервал

где 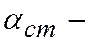коэффициент Стьюдента, принимаемый по табл.10.2 в зависимости от значения доверительной вероятности .

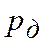Зная 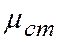, можно вычислить действительное значение изучаемой величины для малой выборки

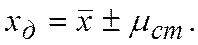
Возможна и иная постановка задачи. По п известных измерений малой выборки необходимо определить доверительную вероятность при условии, что погрешность среднего значения не выйдет за пределы 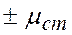. Задачу решают в такой последовательности: вначале вычисляется среднее значение 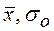и 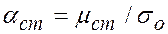. С помощью величины 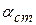, известного п и табл.8.2 определяют доверительную вероятность.

В процессе обработки экспериментальных данных следует исключать грубые ошибки ряда. Появление этих ошибок вполне вероятно, а наличие их ощутимо влияет на результат измерении. Однако прежде чем исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка, а не отклонение вследствие статистического разброса. Известно несколько методов определения грубых ошибок статистического ряда. Наиболее простым способом исключения из ряда резко выделяющегося измерения является правило трех сигм: разброс случайных величин от среднего значения не должен превышать

Более достоверными являются методы, базируемые на использовании доверительного интервала. Пусть имеется статистический ряд малой выборки, подчиняющийся закону нормального распределения. При наличии грубых ошибок критерии их появления вычисляются по формулам

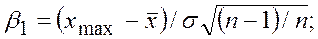
где наибольшее и наименьшее значения из п измерений.

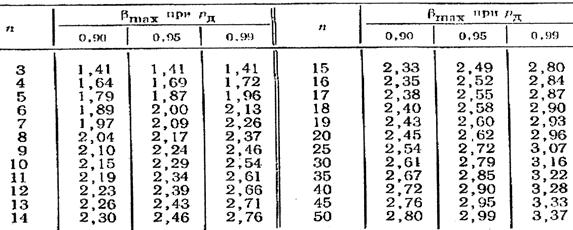
В табл. приведены в зависимости от доверительной вероятности максимальные значения , возникающие вследствие статистического разброса. Если 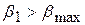, то значение 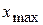необходимо исключить из статистического ряда как грубую погрешность. При 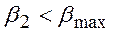исключается величина 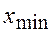. После исключения грубых ошибок определяют новые значения 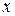и и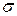з или измерений.

Таблица

Критерий появления грубых ошибок

Дата добавления: 2014-01-07