Теоремы о подобии. Критерии механического и гидродинамического подобия

Первая теорема подобия. У подобных явлений можно найти сочетания параметров, называемые критериями подобия, имеющими одинаковые значения. Справедливо и обратное положение: если критерии подобия численно одинаковы, то явления подобны.

Рассмотрим различные применения первой теоремы:

случай подобных процессов, описываемых однородными уравнениями

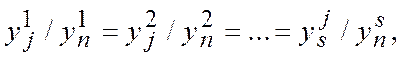
где 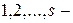- номера процесса; - параметры соответственно модели и объекта. Индексы, характеризующие номер процесса, можно опустить и записать в общем виде:

idem,

где idem означает «соответственно одинаково для всех рассмотренных процессов»; критерии подобия.

Критерии подобия любого явления могут преобразовываться в критерии другой формы с помощью операций умножения или деления ранее найденных критериев друг на друга. Так, если какие-либо критерии = idem и 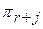= idem, то = idem; = ide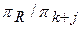m; = idem, 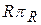= idem, где R - любая постоянная величина.

Если уравнения процесса характеризуют его протекание во времени и пространстве с доступной и необходимой для данного исследования полнотой, то в этом случае приведенные условия являются критериями полного подобия. Если уравнения характеризуют протекание процесса или только во времени, или только в пространстве, то формируются критерии неполного подобия. Наконец, если исходные уравнения перед определением критериев будут упрощены, в них будут отброшены какие-то заведомо влияющие факторы и т.д. то найденные из них критерии будут называться критериями приближенного подобия.

В случае подобных процессов, описываемых уравнениями с неоднородными функциями (трансцендентные, сложные и т.д.), аргументы неоднородных функции должны быть равны, так как они в этом случае являются критериями подобия. Так, например, если в функциях 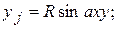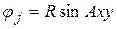выполняется условие , то подобие процессов характеризуется равенством 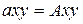. Возможны условно подобные процессы, подобие которых выполняется при введении переменных масштабов (квазиподобие).

Первая теорема о подобии справедлива и в более сложных случаях, когда уравнения процессов на первый взгляд неодинаковы, но введение переменных масштабов параметров времени или пространства дает возможность установить соответствие между оригиналом и моделью. Возможны, например, два случая подобия; обычное геометрическое, когда куб преобразуется в подобный куб (другого размера), и так называемое афинное, когда куб преобразуется в параллелепипед.

Вторая теорема подобия. Всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено в виде зависимости между безразмерными соотношениями из входящих в уравнение параметров, которые и есть критерии подобия.

Теорема указывает на возможность замены переменных и сокращения их числа от 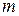размерных до 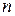безразмерных величин, с переходом к критериальному уравнению. Таким образом, упрощается обработка аналитических и экспериментальных исследований, так как связь между безразмерными критериями подобия чаще всего проще. Переход к безразмерным соотношениям позволяет распространить результаты исследования, проведенного применительно к конкретному явлению, на ряд подобных явлений.

Третья теорема подобия. Необходимыми и достаточными условиями подобия являются пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия изучаемого явления.

Три общие теоремы о подобии дополняются положениями, оказавшимися весьма существенными при решении многих практических задач.

Однако к теоремам подобия имеется ряд дополнительных положений, которыми необходимо руководствоваться при моделировании.

Дополнительные положения.

1. Подобие сложных систем, состоящих из нескольких подсистем, соответственно подобных в отдельности, обеспечивается подобием всех сходственных элементов, являющихся общими для подсистем. Как следствие этого положения утверждается, что подобные сложные системы остаются подобными после любых упрощений, если только эти упрощения были проведены в системах соответственно одинаково.

2. Все теоремы и условия подобия, справедливые для систем различной сложности, могут быть распространены на нелинейные системы или системы с переменными параметрами, если выполняются условия совпадения относительных характеристик, сходственных параметров, являющихся нелинейными или переменными.

3. Условия подобия, справедливые для изотропных систем, которые характеризуются одинаковостью физических свойств по всем координатам внутри данной системы, могут быть распространены и на анизотропные системы, имеющие неодинаковые свойства по различным направлениям. При этом относительные анизотропии в сравниваемых системах должны быть соответственно одинаковы.

4. В системах, геометрически не подобных, но имеющих нелинейное подобие пространства, процессы могут быть физически подобны, имея в сходственных точках пространства подобные изменения параметров процесса.

5. Все условия подобия, относящиеся к детерминированно заданным системам, справедливы для стохастически определенных систем при условии совпадения у этих систем плотностей вероятностей сходственных параметров, представленных в виде относительных характеристик. При этом дисперсии и математические ожидания всех параметров с учетом масштабов должны быть у подобных систем одинаковыми. Дополнительным условием подобия является выполнение требования физической реализуемости сходственной корреляции между стохастически заданными параметрами, входящими в условие однозначности.

14. Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях.

Анализ случайных погрешностей основывается на теории случайных ошибок, дающих возможность с определенной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки.

Основу теории случайных ошибок составляют предположения о том, что при большом числе измерении случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто: большие погрешности встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины); при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерении, а появление того или иного результата измерения как случайного события описывается нормальным законом распределения.

Различают генеральную и выборочную совокупность измерений. Под генеральной совокупностью подразумевают все множество возможных значений измерений или возможных значений погрешностей 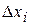. Для выборочной совокупности число измерений 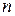ограничено, и в каждом конкретном случае строго определяется. Обычно считают, если 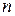>30, то среднее значение данной совокупности измерений 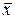достаточно приближается к его истинному значению.

Теория случайных ошибок позволяет оценить точность и надежность измерения при данном количестве замеров или определить минимальное количество замеров, гарантирующее требуемую (заданную) точность и надежность измерений. Наряду с этим возникает необходимость исключить грубые ошибки ряда, определить достоверность полученных данных и др.

15. Интегральная оценка с помощью доверительной вероятности.

Для большой выборки и нормального закона распределения общей оценочной характеристикой измерения являются дисперсия D и коэффициент вариации :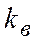

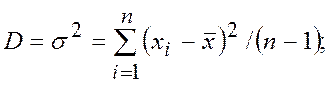
Дисперсия характеризует однородность измерения. Чем выше D, тем больше разброс измерений. Коэффициент вариации характеризует изменчивость. Чем выше , тем больше изменчивость измерений относительно средних значений, 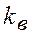оценивает также разброс при оценке нескольких выборок.

Доверительным называется интервал значений 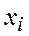, в который попадает истинное значение измеряемой величины с заданной вероятностью. Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону . Эта величина определяется в долях единицы или в процентах. Доверительная вероятность описывается выражением

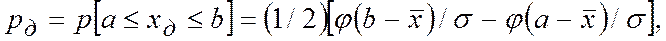
где - интегральная функция Лапласа (табл.1), определяемая выражением

Аргументом этой функции является отношение к среднеквадратичному отклонению 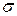, т.е.

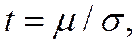
где - гарантийный коэффициент;

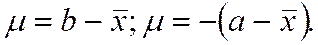
Таблица 1

Интегральная функция Лапласа

Если же на основе определенных данных установлена доверительная вероятность 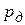(часто ее принимают равной 0,90; 0,95; 0,9973), то устанавливается точность измерений (доверительный интервал 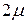) на основе соотношения . Половина доверительного интервала равна

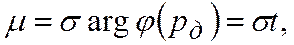
где - аргумент функции Лапласа, а при 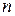<30 -функции Стьюдента (табл.2). Доверительный интервал характеризует точность измерения данной выборки, а доверительная вероятность - достоверность измерения. Пусть, например, выполнено 30 измерений прочности дорожной одежды участка автомобильной дороги при среднем модуле упругости одежды =170 МПа и вычисленном значении среднеквадратического отклонения 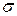= 3,1 МПа.

Требуемую точность измерений можно определить для разных уровней доверительной вероятности (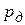=0,9; 0,95; 0,9973), приняв значения t по табл.1. В этом случае соответственно = ±3,1×1,65=5,1; ±3,1×2,0 = 6,2; ±3,1×3,0 = 9,3 МПа. Следовательно, для данного средства и метода доверительный интервал возрастает примерно в два раза, если увеличить 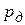только на 10 %.

Если необходимо определить достоверность измерений для установленного доверительного интервала, например = ±7 МПа, то = 7/3,1 = 2,26. По табл.1 для t = 2,26 определяем 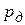= 0;97. Это означает, что в заданный доверительный интервал из 100 измерений не попадают только три.

Таблица 2

Коэффициент Стьюдента

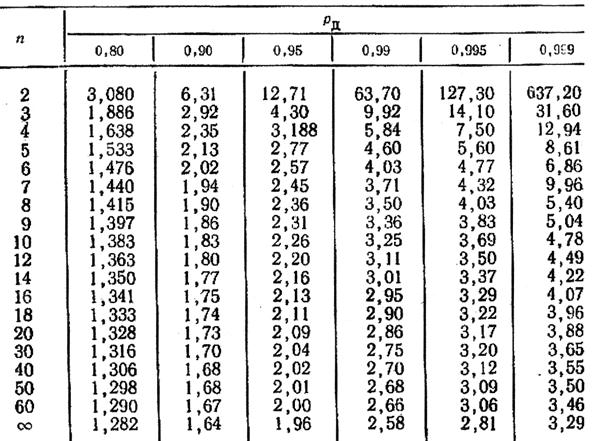
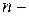число параллельных серий опытов

Значение называют уровнем значимости. Из него следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из 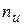измерений, где или иначе приходится браковать одно из измерений.

По данным приведенного выше примера можно вычислить количество измерений, из которых одно измерение превышает доверительный интервал. При 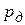= 0,9; определяется 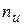= 0,9/(1 - 0,9) = 9 измерений. При 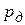равной 0,95 и 0,9973, соответственно 19 и 367 измерений.

Дата добавления: 2014-01-07