Лекция №6 Взаимосвязанные системы регулирования. Системы несвязанного и связанного (автономного) регулирования

Вопросы, рассматриваемые в лекции:

1. К каким последствиям приводит равенство динамики прямых и перекрестных связей в АСР несвязанного регулирования.

2. Какие рабочие частоты желательно иметь в контурах несвязанного регулирования.

3. Что такое комплексный коэффициент связанности.

4. Принцип автономности.

5. Условие приближенной автономности.

Объекты с несколькими входами и выходами, взаимно связанные между собой, называют многосвязанными объектами.

Динамика многосвязанных объектов описывается системой дифференциальных уравнений, а в преобразованном по Лапласу виде матрицы передаточных функций.

Существует два различных подхода к автоматизации многосвязанных объектов: несвязанное регулирование отдельных координат с помощью одноконтурных АСР; связанное регулирование с применением многоконтурных систем, в которых внутренние перекрестные связи объекта компенсируются внешними динамическими связями между отдельными контурами регулирования.

Рисунок 1 - Структурная схема несвязанного регулирования

При слабых перекрестных связях расчет несвязанных регуляторов ведут, как для обычных одноконтурных САР с учетом основных каналов регулирования.

Если перекрестные связи достаточно сильны, то запас устойчивости системы может оказаться ниже расчетного, что приводит к снижению качества регулирования или даже к потери устойчивости.

Для учета всех связей объекта и регулятора, можно найти выражение для эквивалентного объекта, которое имеет вид:

W₁^э(p) = W₁₁(p) + W₁₂(p)*R₂(p)*W₂₁(p) / [1 - W₂₂(p)*R₂(p)]. (1)

Это выражение для регулятора R₁(p), аналогичное выражение и для регулятора R₂(p).

Если рабочие частоты двух контуров сильно отличаются друг от друга, то взаимное их влияние будет незначительным.

Наибольшую опасность представляется случай, когда все передаточные функции равны между собой.

W₁₁(p) = W₂₂(p) = W₁₂(p) = W₂₁(p). (2)

В этом случае настройка П - регулятора будет в два раза меньше, чем в одноконтурной АСР.

Для качественной оценке взаимного влияния контуров регулирования используют комплексный коэффициент связности.

K_св (ίω) = W₁₂(ίω)*W₂₁ (ίω) / W₁₁(ίω)*W₂₂(ίω). (3)

Его обычно вычисляют его на нулевой частоте и рабочих частотах обоих регуляторов.

Основой построения систем связанного регулирования является принцип автономности. Применительно к объекту с двумя входами и выходами понятие автономности означает взаимную независимость выходных координат У₁ и У₂ при работе двух замкнутых систем регулирования.

По существу, условие автономности складывается из двух условий инвариантности: инвариантности первого выхода У₁ по отношению к сигналу второго регулятора Х_P2 и инвариантности второго выхода У₂ по отношению к сигналу первого регулятора Х_P1:

y₁(t,x_P2)=0; y₂(t,x_P1)=0; "t, x_P1, x_P2 . (4)

При этом сигнал Х_P1 можно рассматривать как возмущение для У₂, а сигнал Х_P2 – как возмущение для У₁. Тогда перекрестные каналы играют роль каналов возмущения (рисунок 1.11.1 и рисунок 1.11.2). Для компенсации этих возмущений в систему регулирования вводят Динамические устройства с передаточными функциями R₁₂(p) и R₂₁(p), сигналы от которых поступают на соответствующие каналы регулирования или на входы регуляторов.

По аналогии с инвариантными АСР передаточные функции компенсаторов R₁₂(p) и R₂₁(p), определяемые из условия автономности, будут зависеть от передаточных функций прямых и перекрестных каналов объекта и будут равны:

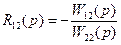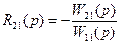; , (5)

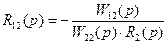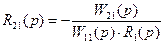; . (6)

Так же, как в инвариантных АСР, для построения автономных систем регулирования важную роль играет физическая реализуемость и техническая реализация приближенной автономности.

Условие приближенной автономности записывается для реальных компенсаторов с учетом рабочих частот соответствующих регуляторов:

при w=0; w=w_Р2, (7)

при w=0; w=w_Р1. (8)

(а) – компенсация воздействия от второго регулятора в первом контуре регулирования

(б) – компенсация воздействия от первого регулятора во втором контуре регулирования

Рисунок 2 - Структурные схемы автономных АСР

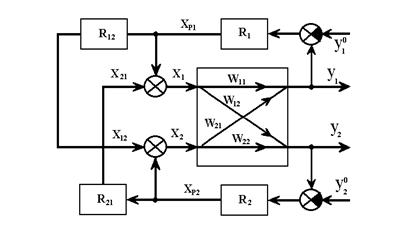
Рисунок 3 - Структурная схема автономной системы регулирования двух координат

В химической технологии одним из самых сложных многосвязных объектов является процесс ректификации. Даже в простейших случаях – при разделении бинарных смесей – в ректификационной колонне можно выделить несколько взаимосвязанных координат. Например, для регулирования процесса в нижней части колонны необходима стабилизация минимум двух технологических параметров, характеризующих материальный баланс по жидкой фазе и по одному из компонентов.

Вопросы для самоконтроля:

1. Определение и задачи автоматизации.

2. Современная АСУТП и этапы ее развития.

3. Задачи управления и регулирования.

4. Основные технические средства автоматики.

5. Технологический процесс, как объект управления, основные группы переменных.

6. Анализ технологического процесса как объекта управления.

7. Классификация технологических процессов.

8. Классификация систем автоматического регулирования.

9. Функции управления автоматических систем.

10. Выбор регулируемых величин и регулирующего воздействия.

11. Анализ статики и динамики каналов управления.

12. Анализ входных воздействий, выбор контролируемых величин.

13. Определение уровня автоматизации ТОУ.

14. Объекты управления и их основные свойства.

15. Разомкнутые системы регулирования. Достоинства, недостатки, область применения, структурная схема.

16. Замкнутые системы регулирования. Достоинства, недостатки, область применения, структурная схема и пример использования.

17. Комбинированные системы регулирования. Достоинства, недостатки, область применения, структурная схема и пример использования.

18. Теория инвариантности автоматических систем управления.

19. Комбинированные АСР.

20. Типовые компенсаторы.

21. Расчет компенсатора.

22. Что такое условие приближенной инвариантности.

23. На каких частотах проводят расчет компенсатора при условии частичной инвариантности.

24. Условие физической реализуемости инвариантных САР.

25. Системы каскадного регулирования.

26. Что такое эквивалентный объект в каскадной САР.

27. Чем объясняется эффективность каскадных АСР.

28. Методы расчета каскадных АСР.

29. АСР с дополнительным импульсом по производной из промежуточной точки.

30. Область применения АСР с дополнительным импульсом по производной.

31. Расчет АСР с дополнительным импульсом по производной.

32. Взаимосвязанные системы регулирования. Системы несвязанного регулирования.

33. К каким последствиям приводит равенство динамики прямых и перекрестных связей в АСР несвязанного регулирования.

34. Какие рабочие частоты желательно иметь в контурах несвязанного регулирования.

35. Что такое комплексный коэффициент связанности.

36. Системы связанного регулирования. Автономные АСР.

37. Принцип автономности.

38. Условие приближенной автономности.

Дата добавления: 2014-01-07