Теорема о движении центра масс системы

Центр масс системы — это геометрическая точка, радиус-вектор которой определяется по формуле, а ее координаты по формулам

.

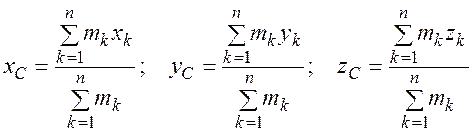где 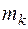— масса каждой k - й точки (или тела); — координаты k – й точки или центра тяжести k - го тела, входящих в механическую систему; 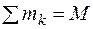— масса всей системы.

Центр масс механической системы движется как любая материальная точка, масса которой равна массе всей меха­нической системы и к которой приложена сила, равная главному вектору внешних сил.

Доказательство. Основное уравнение динамики для k - й материальной точки

.

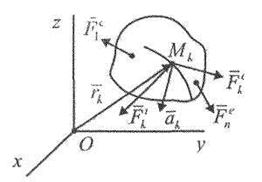
Для всей механической системы

,

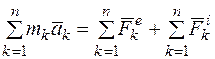где 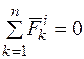— по свойству внутренних сил,

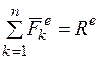— главный вектор всех внешних сил, приложенных к системе,

.

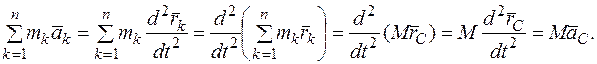
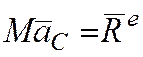Уравнение может быть записано в скалярной форме в проекциях на оси декартовых координат или на естественные оси. В декартовых осях имеет вид

.

Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс механической системы дви­жется 1.равномерно и прямолинейно или 2.покоится.

2. Если проекция главного вектора внешних сил, действующих на систему, на какую-либо ось равна нулю, то проекция центра масс на эту ось либо 1.покоится, 2.либо движется равномерно, т,е., если , то .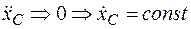

3. Если в начальный момент система покоилась, то — проекция центра масс покоится. При 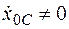центр масс будет двигаться вдоль оси х с постоянной скоростью.

Эти следствия выражают закон сохранения движения цен­тра масс механической системы. При 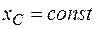справедливо равенство

.

где — приращение координаты центра масс k ~го тела при изменении положения тел в механической системе, равное проекции абсолютного перемещения этой точки на ось х

Задача 1. К концу троса, навитого на барабан, подвешен груз массы 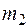= 20 кг. Барабан массы =10 кг может вра­щаться вокруг горизонталь­ной оси. Определить реак­цию оси, если груз начнет двигаться с постоянным уско­рением = 2 м/с ².

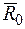Решение. Покажем внеш­ние силы — вес барабана , вес груза реакцию оси О. Запишем теорему о движении центра масс механической системы:

.

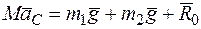Выберем начало оси х в точке О и направим ее вниз. Спро­ецируем векторное равенство на эту ось:

.

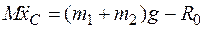Отсюда

.

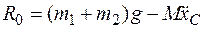Запишем координату центра масс:

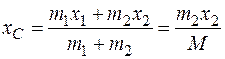, т. к. 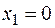, а .

Продифференцируем дважды, определим ускорение центра масс:

.

Тогда

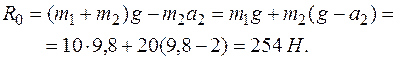
Задача 2. Призма А массы = 2 кг покоится на гладкой горизон­тальной плоскости. По наклонной плоскости призмы из со­стояния покоя начинает перемещаться груз В массы 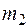= 1 кг. Пренебрегая размерами груза, определить перемещение приз­мы, когда он переместится на расстояние l = 30 см; 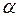= 30°).

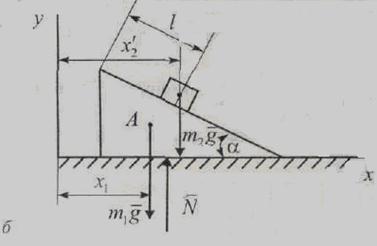
Решение. Внешние силы, действующие на систему: вес призмы, вес груза и нормальная реакция плоскости (рис. 53, б).

Теорема о движении центра масс

.

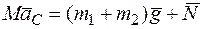Так как 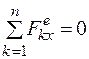(все силы перпендикулярны оси х), то

,

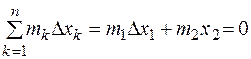где .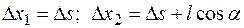

=

Призма переместится влево на 8,7 см.

Дата добавления: 2014-01-14