Следствия из теоремы

Теорема в интегральной (конечной) форме. Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов всех внешних сил, действующих на точки механической системы, за тот же промежуток времени.

Механической системы в дифференциальной форме. Производная по времени от главного вектора количеств движения механической системы равна геометрической сумме внешних сил, действующих на эту систему.

Теорема об изменении главного вектора количества движения

Доказательство. На любую k - ю точку механической систе­мы действуют силы 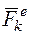и . Для этой точки

.

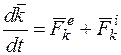Для всей системы

,

где

.

В проекциях на оси декартовых координат имеет вид

. (4.22)

Следствия из теоремы:

1. Если 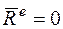, то .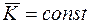

2. Если проекция главного вектора на какую-либо ось равна нулю, то проекция количества движения на эту ось есть величина постоянная. Например, , то .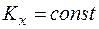

Доказательство.

.

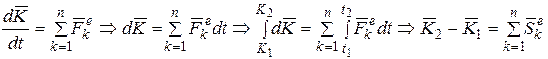где - импульс главного вектора внешних сил.

Векторному равенству соответствуют три равенства в скалярной форме

.

1. Если 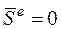, то .

2. Если 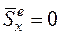, то .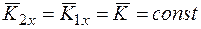

Задача 5.. Лодка массы М = 200 кг, на корме которой стоял человек массы т = 80 кг, двигалась со скоростью м/с. Затем че­ловек спрыгнул с лодки со скоростью u = 4 м/с против ее дви­жения. С какой скоростью V после этого будет двигаться лодка?

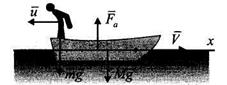
Решение. Внешними силами являются вес лодки 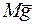, вес человека 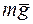и выталкивающая сила . Силой сопро­тивления движению пренебрегаем. Все силы перпендикулярны оси х. Поэтому

.

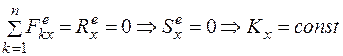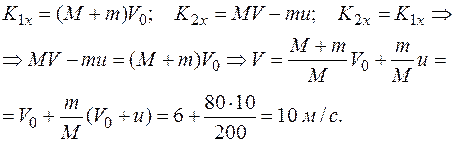
Базовые вопросы

1. Свойства внутренних сил.

2. Что называется а) центром масс механической системы, б) количеством движения точки и механической системы, в) импульсом силы.

3. Что представляют собой дифференциальные уравнения механической системы?

4. Сформулируйте теорему о движении центра масс механической системы.

5. Сущность следствий из теоремы о движения центра масс механической системы.

6. Поясните практическое применение теоремы о движении центра масс механической системы.

7. Сформулируйте теорему об изменении количества точки в дифференциальной и конечной формах.

8. Сформулируйте теорему об изменении количества механической системы в дифференциальной и конечной формах.

Дата добавления: 2014-01-14