Биномиальное распределение. 1. Биномиальное распределение случайной величины

План

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

ЛЕКЦИЯ № 7

1. Биномиальное распределение случайной величины

2. Нормальное распределение

3. Стандартный нормальный закон распределения случайной величины

Ранее в лекции №4 мы рассмотрели формулу Бернулли (4.1), которая позволяет рассчитать вероятность того, что интересующее нас событие при испытаниях произойдет ровно 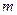раз. При этом предполагалось, что вероятность однократного появления данного события не меняется от опыта к опыту.

Используя формулу Бернулли, можно задать случайную величину – число появления данного события при испытаниях.

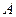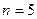Пусть вероятность однократного появления события рана , следовательно, вероятность неудачи . Число испытаний . Рассчитаем вероятности появления данного события , , 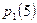, , 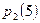, 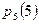и составим таблицу:

	1/32	5/32	10/32	10/32	5/32	1/32

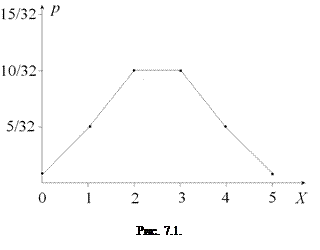
Построим многоугольник распределения данной случайной величины (рис. 7.1).

Распределение величины называется биномиальным распределением с параметрами и .

Найдем математическое ожидание и дисперсию биномиального распределения. Рассмотрим случайную величину X – число появлений события 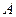в независимых испытаниях. Общее число X появления события 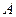в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому, если 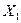– число появления события А в первом испытании, 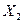- во втором,..., - в -ом, то общее число появлений события:

и

Так как математическое ожидание числа появлений события в одном испытании равно вероятности события, то . Ряд распределений величины будет иметь вид:

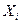
P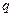

Следовательно, 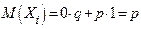. Итак, .

Для дисперсии имеем: .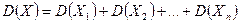

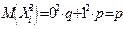
тогда , .

Таким образом, если случайная величина имеет биномиальное распределение, то ее математическое ожидание, дисперсия и среднее квадратичное отклонение вычисляются по следующим формулам:

(7.1)

Дата добавления: 2014-01-14