Гиперграфы. Использование теории графов для описания моделей систем управле­ния со сложной структурой, стало распространенным в последнее время

Графы

Использование теории графов для описания моделей систем управле­ния со сложной структурой, стало распространенным в последнее время. Теоретико-графовая форма описания модели позволяет эффективно использовать новые возможности языков программирования, такие как указатели, списки, классы, множест­венное наследие. Представление в форме ориентированного (сигнального) графа, в частности структурной схемы, расширяет ин­формацию о модели, по сравнению с НФК и СНДУ, позволяя вводить причинно-следственные отношения. Знание о направленности связей имеет большое значение для задач анализа и синтеза.

В качестве иллюстрации на рис. 1.1. приведена диаграмма графа модели странного аттрактора Лоренца [93]. Эта форма представления позволяет эффективнее решать задачи выделения путей и ко­нтуров, связности, структурной управляемости и многие другие, чем в форме НФК и отчасти СНДУ.

Модель системы представляется ориентированным графом H=<G,H> с множеством переменных Х=x1,...., xn, N - общее множество вершин, и множеством дуг G - упорядоченных пар номеров смежных вершин (i,j), G=(i,j)1,... (i,j)n. Общее количество таких пар обозначено в приме­рах как Q.

Несмотря на всю компактность и удобство такой записи, на практике чаще используют матрицу смежности R = rij, показывающую наличие дуги между i-ой и j-ой вершинами.

Рис. 1.1. Модель странного аттрактора в форме ориентированного графа

Рис. 1.2. Модель системы в форме графа

Рис. 1.3. Модель системы в форме гиперграфа

Рис. 1.4. Модель странного аттрактора в форме гиперграфа

Другим способом представления топологии является матрица изоморфности D, в строках которой представлены номера входящих (с плюсом) и выходящих (с минусом) дуг.

Для приведенного на рис. 1.2 примера матрицы смежности и изоморфности имеют вид:

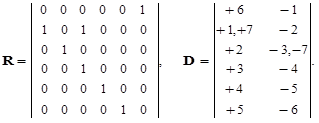
Избыточность хранимой информации в матрице смежности (нулевые значения) компенсируют­ся простотой вычислительных алгоритмов и скоростью получения требуемой ин­формации из матрицы. Кроме того, наличие только двух значений 0 или 1, дает возможность использовать для ее представления битовые поля, что дает значительную экономию памяти, и при размерах системы порядка 100 элементов не уступает по затратам ресурсов на хранение матрицы изоморфности, при значительно более простых алгоритмов обработки информации. Использование матриц смежности, инцидентностей, достижимостей и др. имеет большое применение для алгоритмов топологи­ческого анализа СС НСУ [107].

Ориентированные графы (структурные схемы) обычно широко используются при описании линейных систем и систем с одновходовыми нелинейностями. Однако возникают некоторые затруднения при описании нелинейных систем, где нелиней­ные функции могут зависеть от нескольких переменных, например при описании операций умножения и деления.

Гиперграф являются теоретико-множественной формой представления дифференциальных уравнений, заданных в общем случае непричинно—следственным способом [53, 54, 56, 73]. По сравнению с графом, представление модели в форме гиперграфа расширяет возможности представления многовходовых элементов, од­нако при этом теряется информация о направленности связей.

Гиперграф определяется как пара H = < X, E > образующая конечное множество X=x1,...,xn вершин и некоторое семейством E=e1,...,eq ребер - непустых частей Х, удовлетворяющих условию UE=X [67]. Одним из способов задания топологии гиперграфа [53], является матрица 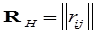, где

Гиперграф является вариантом симплециального комплекса или симплециальной схемы. В ряде работ [75], вводится понятие ориентированного гиперграфа. При этом множество E - определяется как множество ориентированных ребер.

Примеры гиперграфов приведены на рис. 1.5 и рис. 1.6. Из диаграмм видно, что гиперг­раф является способом группирования зависимых переменных, без указания причинно-следственных отношений между ними.

При этом способе внутреннего представления модели в ЭВМ, также возникают проблемы при внешнем представлении Скорее можно предлагать автоматическое построение гиперграфа по введенной системе уравнений.

Дата добавления: 2014-01-14