Аксиомы теории вероятностей и их следствия. Правило сложения вероятностей

Пусть производится некоторый опыт со случайным исходом. Рассмотрим множество 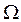всех возможных исходов опыта; каждый его элемент 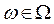будем называть элементарным событием, а все множество 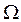- пространством элементарных событий.

Опр. Если событие А распадается на несколько непересекающихся подмножеств 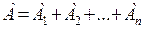, то будем называть события 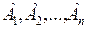“ вариантами ” события А.

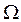- достоверное событие.

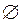- невозможное событие.

Примечание: Как уже отмечалось есть два вида определений одного и тогоже: математическое и логическое. Первое удобно при решении задач, второе предназначено для описания реальных событий.

Опр. Говорят, что несколько событий в данном опыте образуют полную группу, если в результате опыта неизбежно должно появиться хотя бы одно из них.

Опр. Несколько событий 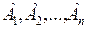образуют полную группу если .

Опр. Несколько событий в данном опыте называются несовместными, если никакие два из них не могут появиться вместе.

Опр. Два события А и В называется несовместными если

Опр. Несколько событий 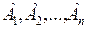называются попарно несовместными если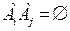

Опр.Противоположным событию А называется событие состоящее в не появлении события А.

Пример: А - выпадение герба

- не выпадение герба

Опр.Суммой двух событий А и В называется событие С, состоящее в выполнении события А или В, или обоих событий вместе.

Опр.Произведением двух событий А и В называется событие, состоящее в выполнении событий А и В вместе.

Примечание: Математические определения суммы и произведения событий приведены в параграфе 2.2.

Аксиомы теории вероятностей.

Пусть каждому событию А ставится в соответствии некоторое число, называемое вероятностью события.

1. Вероятность любого события заключена между нулём и единицей:

2. Если А и В несовместные события 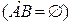, то

Обобщая

3. Если имеется счётное множество несовместных событий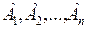,..., то

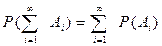
Опр. События 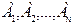называются равновозможными, если

Следствие аксиом:

Опр.Благоприятным случаем событию А называется случай влекущий за собой данное событие А.

“Классическая” формула подсчёта вероятностей:

Теорема:

Пусть результаты опыта могут быть представлены в виде группы событий удовлетворяющих условиям:

1. (образуют полную группу)

2. 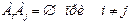(попарно несовместные)

3. 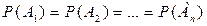(равновозможные).

Пусть есть из этих событий благоприятны событию А

тогда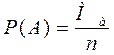

Доказательство:

Т. к. образуют полную группу, то 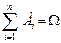, и следует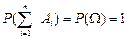

Т. к. 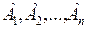несовместны, то

Объединяем выше сказанное

Т. к. 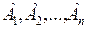равновозможны, то

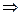
Следствие 1.

Сумма вероятностей полной группы несовместных событий равна единице, т. е. если

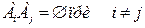и то

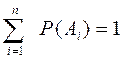
Дополнение: Сумма вероятностей противоположных событий равна единице

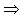
Следствие 2. Правило сложения вероятностей.

Если события А и В совместны , то

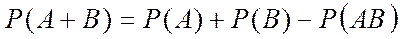
Доказательство:

Представим

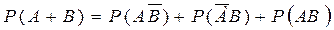
но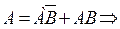

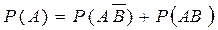
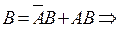
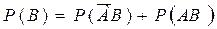
откуда

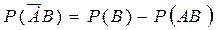
подставляем и получим

Аналогично получим.

Дата добавления: 2014-01-14